Dauerfestigkeitsauswertung: Das Probit Verfahren zur experimentellen Ermittlung der Dauerfestigkeit

Um Wöhlerlinien experimentell richtig ermitteln zu können, muss neben der Zeitfestigkeit auch die Dauerfestigkeit ausgewertet werden. Neben dem Treppenstufenverfahren nach Hück wird hier häufig das Probitverfahren genutzt. Dieses wird in diesem Artikel vorgestellt.
In diesem Artikel lernen Sie,
- Wie Sie das Probitverfahren richtig anwenden indem Sie Ihre Dauerfestigkeitsversuche danach planen und auswerten
- wann Sie das Probitverfahren anwenden sollten, und wann nicht
- welche weiteren Verfahren es gibt, und wann diese angewandt werden.
Inhalt
Übersicht der Verfahren zu Dauerfestigkeitsauswertung
Für die Auswertung der Versuche im Dauerfestigkeitsbereich stehen verschiedene Verfahren zur Verfügung. Müller hat in seiner Dissertation Link umfangreich untersucht welche Auswerteverfahren die treffsichersten Ergebnisse liefern. Diese Ergebnisse sind auch in die DIN50100 eingeflossen. Untersucht wurde das Treppenstufenverfahren und die Auswertung nach Hück, Maximum Likelihood, Deubelbeiss und Klubberg sowie das Probitverfahren und das Abgrenzungsverfahren.
Bei der Bewertung der Verfahren muss unterschieden werden, ob nur die Mittelwerte σD,50% oder auch die Streuungen (also die Standardabweichungen sσ ) ermittelt werden sollen. Für die Auswertung von Mittelwerten sind alle Verfahren geeignet. Die nötigen Stichprobenumfänge sind überschaubar. Anders sieht dies bei der Auswertung der Streuungen aus. Um hier treffsichere Aussagen liefern zu können, sind die erforderlichen Stichprobenumfänge teilweise sehr hoch.
Empfehlungen
Für die Auswertung der Dauerfestigkeit werden folgende drei Verfahren empfohlen:
- Das Treppenstufenverfahren mit der Auswertung nach Hück liefert neben einer einfachen und robusten Versuchsführung die zuverlässigsten Ergebnisse bei der Auswertung des Mittelwertes.
- Das Abgrenzungsverfahren ist insbesondere für die Auswertung von Streuungen bei kleinen Stichprobenumfängen (n < 40) anzuwenden. Im Vergleich zum Treppenstufenverfahren liefert es vergleichbare Ergebnisse bei der Mittelwertauswertung. Die Versuchsplanung ist jedoch aufwändiger.
- Trotz der schlechteren statistischen Ergebnisse wird außerdem noch auf das Probitverfahren eingegangen, da es eine hohe Verbreitung aufweist.
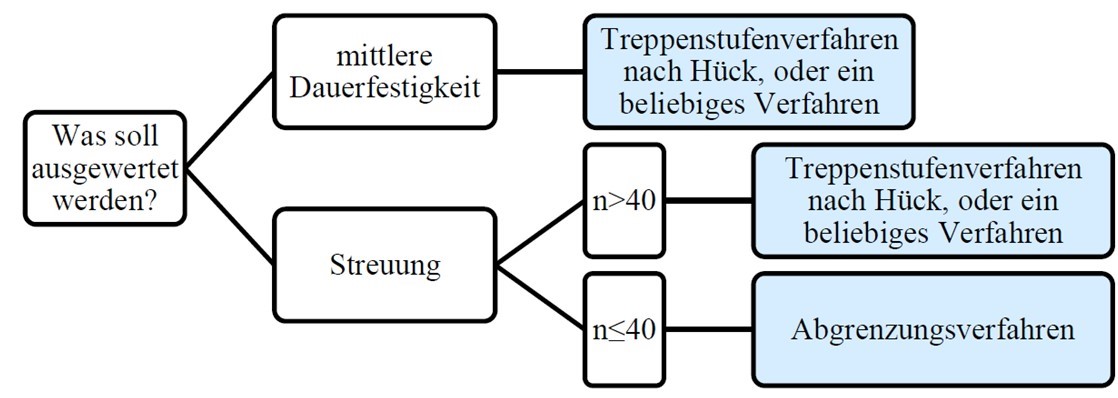
Empfehlung für Verfahren zur experimentellen Auswertung der Dauerfestigkeit
Das Probit Verfahren zur Auswertung der Dauerfestigkeit
Das Probit-Verfahren wurde auf die Betriebsfestigkeit von Mauch und Zenner übertragen. Dieses Verfahren ähnelt dem Abgrenzungsverfahren, da die Auswertung im Wahrscheinlichkeitsnetz erfolgt. Ein Nachteil des Probitverfahrens ist, dass mit mindestens 40 Versuchen vergleichsweise viele Versuche nötig sind, wenn die Streuungen ausgewertet werden sollen. Das Vorgehen besteht aus drei Schritten (vgl. folgende Abbildung):
- Festlegung von mindestens vier Lasthorizonten,
- Durchführung der Versuche,
- Auswertung der Versuche.
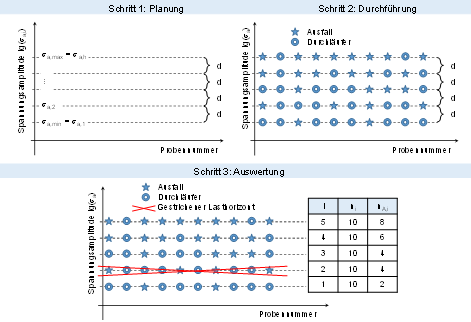
Drei Schritte zur Auswertung der Dauerfestigkeit nach dem Probit Verfahren
Schritt 1a: Festlegung von mindestens 4 Lasthorizonten
Die Wahl der Lasthorizonte ist beliebig. Zur Wahl der Lasthorizonte bietet sich ein logarithmisch konstanter Stufensprung lg(d) an. Der maximale und der minimale Lasthorizont sollten in Abhängigkeit der geschätzten logarithmischen Standardabweichung sσ und der geschätzten Dauerfestigkeit σD,50% gewählt werden. Für die Schätzung der Standardabweichung sσ bieten sich entweder die Erfahrungswerte für Streuungen nach Haibach oder eigene Werte aus vorangegangenen Versuchen an. Die Dauerfestigkeit σD,50% kann z. B. über geeignete Richtlinien (z. B. die FKM-Richtlinie) oder ebenfalls über Erfahrungswerte abgeschätzt werden. Mit den folgenden Gleichungen lassen sich der maximale σa,max und minimale Lasthorizont σa,min berechnen:
lg(σa,min) = lg(σD,50%) - xP ⋅ sσ
lg(σa,max) = lg(σD,50%) + xP ⋅ sσ
Der Verschiebungsfaktor xP wird abhängig von der Anzahl der Lasthorizonte h nach folgender Tabelle bestimmt.
Angabe des Verschiebungsfaktors abhängig von der Anzahl der Lasthorizonte h
| Anzahl Lasthorizonte h | xP |
| 3 | 1 |
| 4 | 1 |
| 6 | 1,5 |
| 8 | 2 |
Eine Berechnung des Stufensprungs lg(d) ist nach folgender Gleichung möglich
lg(d) = (lg(σa,max) - lg(σa,min)) /(h- 1)
lg(d) = (lg(σD,50%) + xP ⋅ sσ – (lg(σD,50%) - xP ⋅ sσ)) / (h - 1)
lg(d) = (2 ⋅ xP ⋅ sσ) /(h - 1)
Die Berechnung der Laststufen erfolgt mit Hilfe folgender Gleichung
lg(d) = lg(σa,i) - lg(σa,i+1) = lg(σa,i / σa,i+1) = konstant
σa,i = σa,i+1 ⋅ di, mit i = …, -3, -2, -1, 0, 1, 2, 3,…
Schritt 1b: Festlegung der Treppenstufen
Als erste Laststufe wird häufig die rechnerisch abgeschätzte Dauerfestigkeit σD* gewählt. Die Treppenstufen (oder auch Lasthorizonte) sollen alle den gleichen Abstand zueinander haben. Dieser Abstand wird als Stufensprung d bezeichnet. Da Wöhlerversuche immer im doppellogarithmischen Netz dargestellt werden, bedeutet dies, dass der logarithmische Stufensprung lg(d) zwischen zwei Spannungsamplituden gleich ist:
lg(d) = lg σa,i - lg σa,i+1 = lg(σa,i/σa,i+1) = konstant = lg(σa,i/σD*)
σa,i = σD* · di
mit
i = ..., -3, -2, -1, 0, 1, 2, 3, ...
σD* = abgeschätzte Dauerfestigkeit (z.B. mittels FKM-Richtlinie)
d = Stufensprung
σa,i = i-te Laststufe
Wird der Stufensprung zu groß gewählt, dann wird die Aussage zu ungenau, da zu wenige Stufen ausgewertet werden können. Bei einer zu kleinen Wahl des Stufensprungs wird der Versuchsaufwand zu groß. Eine gute Wahl des Stufensprungs ist getroffen, wenn für das Verhältnis aus der zu erwartenden Standardabweichung sσ zum logarithmischen Stufensprung lg(d) gilt
lg(d) = sσ ≈ 0,03...0,06.
Da die Standardabweichung vor dem Versuch nicht bekannt ist, muss diese aus Erfahrungswerten möglichst gut geschätzt werden. Dazu bieten sich entweder die Werte nach Haibach (vgl. Link) an oder eigene Werte aus vorangegangenen Versuchen.
Durch Einsetzen der beiden Gelichungen ineinander und Umformen kann der Zusammenhang zwischen der Laststufe σa,i und dem Stufensprung d, bzw. der Standardabweichung sσ berechnet werden:
lg(d) = sσ = lg(σa,i/σD*)
10sσ = σa,i/σD*
σa,i = σD* · 10sσ
mit i = ..., -3, -2, -1, 0, 1, 2, 3, ...
Schritt 2: Durchführung der Versuche
In der Originalarbeit werden mindestens 10 Versuche je Horizont gefordert. Dies führt bei einer gleichzeitigen Forderung nach min. 3 - 4 Horizonten zu einer vergleichsweise hohen Anzahl an Versuchen (ca. 30-40). Bei der Versuchsführung ist darauf zu achten, dass die Anzahl an Proben je Lasthorizont gleich ist.
Eine wesentliche Bedingung ist, dass jeder Lasthorizont mindestens einen Durchläufer enthält. Lasthorizonte auf denen nur Brüche auftreten, sind dem Zeitfestigkeitsgebiet zuzuordnen. Sie werden von der Auswertung ausgeschlossen. Liegen mehrere Lasthorizonte mit nur einem Durchläufer vor, dann darf nur einer für die Auswertung verwendet werden (z. B. der höchste). Die restlichen werden gestrichen (siehe auch obige Abbildung).
Schritt 3: Auswertung der Lasthorizonte
Zur Auswertung der Ergebnisse wird für alle Lasthorizonte die Ausfallwahrscheinlichkeit PA,i berechnet:
PA,i = (3i – 1)/ (3n + 1)
mit
i = nA,i (Anzahl der Ausfälle für den i-ten Lasthorizont) und
n = ni (Anzahl der Versuche für den i-ten Lasthorizont) gilt
PA,i = (3 nA,i – 1)/ (3 ni + 1)
Die Wertepaare aus Ausfallwahrscheinlichkeit PA,i und Lasthorizont σa,i lassen sich jetzt in ein Wahrscheinlichkeitsnetz eintragen (siehe folgende Abbildung). Dabei wird ein Wahrscheinlichkeitsnetz der logarithmischen Normalverteilung angenommen. Dieses Wahrscheinlichkeitsnetz wird anschließend bezüglich der logarithmischen Standardabweichung sσ und der geschätzten Dauerfestigkeit σD,50% ausgewertet.
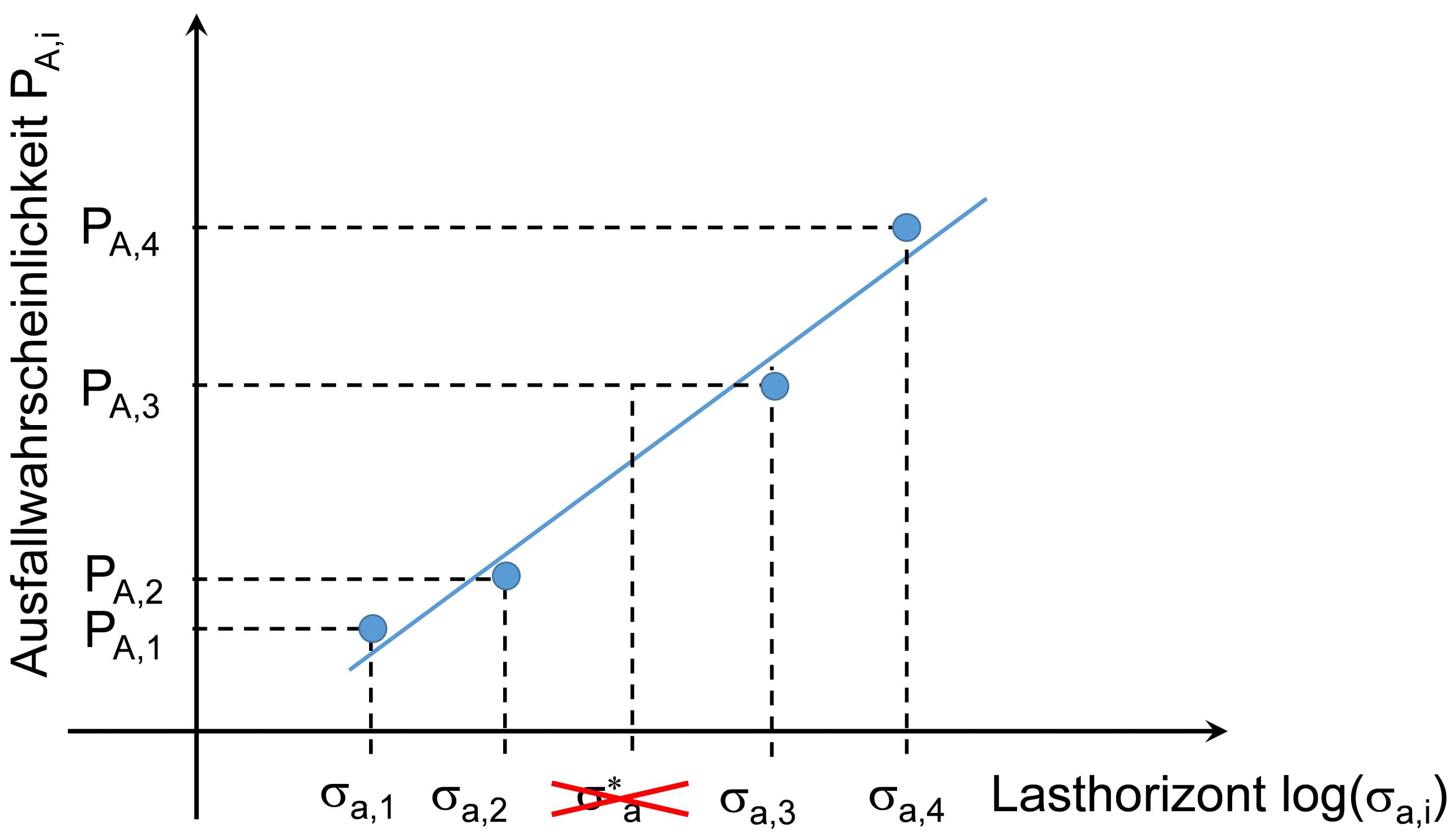
Auswertung der Dauerfestigkeit im Wahrscheinlichkeitsnetz nach dem Probit Verfahren
Auswertung der Dauerfestigkeit im Wahrscheinlichkeitsnetz nach dem Probitverfahren, inkl. des aus der Auswertung ausgeschlossenen Lasthorizontes.
Praxistipp: Für die Auswertung im Wahrscheinlichkeitsnetz finden Sie hier auch wieder ein Excel-Tool.
Auf den Punkt:
Für die Auswertung der Dauerfestigkeit liegen mehrere Verfahren vor. Die bekanntesten sind das Treppenstufenverfahren mit der Auswertung nach Hück oder Maximum Likelihood, das Abgrenzungsverfahren und das Probitverfahren.
Standardabweichung sσ und der geschätzten Dauerfestigkeit σD,50%
Üblicherweise werden bei der Auswertung der Dauerfestigkeit zwei Ziele verfolgt. Einerseits die Ermittlung der mittleren Dauerfestigkeit σD,50% und die Bestimmung der logarithmischen Standardabweichung sσ.
Soll die mittlere Dauerfestigkeit σD,50% ermittelt werden, so sind alle Methoden zuverlässig anwendbar. Auf Grund einer einfachen Handhabung und robusten Versuchsführung werden das Treppenstufenverfahren nach Hück und wegen der weiten Verbreitung das Probitverfahren empfohlen.
Ist die logarithmische Standardabweichung von Interesse, dann bietet sich insbesondere für kleine Stichprobenumfänge ( ) das Abgrenzungsverfahren an. Der Vorteil liegt darin, dass die beiden Auswertehorizonte relativ weit entfernt von der mittleren Dauerfestigkeit platziert werden. Dadurch ist die Auswertung robuster. Für größere Stichproben kann auch das Treppenstufenverfahren angewandt werden.
| Dauerfestigkeit | Standardabweichung | |||
| Treppenstufenverf. nach Hück | ++ | ++ | + | ++ |
| Treppenstufenverf. Max. Likelihood | + | ++ | + | ++ |
| Abgrenzungsverfahren | + | ++ | ++ | ++ |
| Probitverfahren | + | ++ | - | + |
Generell gilt:
- Das Treppenstufenverfahren nach Hück als robustes und einfach anwendbares Verfahren wird besonders empfohlen. Wegen der breiten Verbreitung kann für die Ermittlung der mittleren Dauerfestigkeit auch das Probit Verfahren empfohlen werden.
- Je geringer der Versuchsumfang n ist, umso mehr Aufwand sollte für die Versuchsplanung spendiert werden. Das bedeutet eine möglichst genaue Berechnung der Dauerfestigkeit und eine Schätzung der logarithmischen Standardabweichung. Diese Werte helfen bei der Wahl der Stufensprünge und des Startwertes. Die Dauerfestigkeit wird idealerweise mit Hilfe von Richtlinien wie der FKM-Richtlinie* berechnet oder auf Basis von Erfahrungen geschätzt. Die logarithmische Standardabweichung sollte mit Hilfe eigener Erfahrungen oder über die Erfahrungswerte nach Haibach geschätzt werden.
Weiterführende Informationen zur FKM Richtlinie
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminare zur Versuchsauswertung (und Planung) von Wöhlerlinien und Dauerfestigkeiten:
Ermitteln Sie Ihre Werkstoffkennwerte wie Wöhlerlinien oder Dauerfestigkeiten selber oder lassen sie diese extern ermitteln? Und sind Sie dabei auch immer wieder mit hohen Kosten, kleinen Stichproben und Ausreißern konfrontiert?
Wenn Sie dafür eine schnelle und praktische Lösung suchen, und gerne Ihre Wöhler- oder Dauerfestigkeitsversuche effizient planen und selbständig auswerten wollen, dann ist unser neues zweitägiges Seminar Werkstoffkennwerte der Betriebsfestigkeit (für Simulation und Auslegung) einfach ermitteln und anwenden genau richtig für Sie.
Hier lernen Sie
- Dauerfestigkeiten mit Hilfe statistischer Verfahren auszuwerten
- Wöhlerlinien statistisch zu interpretieren
- Streuungen zu berechnen und Sicherheitszahlen abzuleiten
- mit kleinen Stichprobenumfängen umzugehen und
- Ausreisser zu bewerten
- welche Versuchstechnik es zur Ermittlung statischer Werkstoffkennwerte und für die Schwingprüfung gibt
- alle wichtigen Werkzeuge kennen und in umfangreichen Übungen anwenden
- anhand statistischer Tests Wöhlerkurven und Dauerfestigkeiten miteinander zu vergleichen
- wie Ihnen moderne Regelwerke wie die FKM Richtlinie bei der Versuchsplanung helfen können.
Weiterführende Literatur
Um Wöhlerkurven und Dauerfestigkeiten statistisch auszuwerten und zu planen, bietet sich außerdem unser
Buch Statistik der Betriebsfestigkeit an.
dieses führt Sie schnell und verständlich in die Versuche und die Statistik Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auswertung von Versuchen der Betriebsfestigkeit wie Wöhlerlinien.
