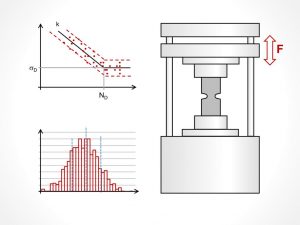
Geeignete Sicherheitsfaktoren müssen die Streuungen der Werkstoffdaten und den Umfang der Versuche berücksichtigen. Ich zeige Ihnen eine einfache und schnelle Methode dazu, die jeder umsetzen kann.
Bei der Auslegung eines Bauteiles sind aufgrund der Streuungen Sicherheiten vorzuhalten um die gewünschten Ausfallwahrscheinlichkeiten garantieren zu können. Basiert die Bauteilauslegung auf Werkstoffkennwerten (z. B. Zugfestigkeit oder Wöhlerlinie), die durch eigene Versuche ermittelt wurden muss zusätzlich noch die Unsicherheit auf Grund der Stichprobenanzahl berücksichtigt werden.
Die Sicherheit setzt sich damit aus zwei Teilen zusammen:
Der Sicherheit bezüglich der Ausfallwahrscheinlichkeit jPA
Die Sicherheit bezüglich des Stichprobenrisikos jn (in diesem Artikel erfahren Sie, wie dieser berechnet wird)
Die gesamte Sicherheit j ist das Produkt dieser beiden Sicherheiten:
j= jPA∙jn.
Oder anders ausgedrückt gilt für die Lebensdauer bei einer beliebigen Ausfallwahrscheinlichkeit:
Lebendauerx % Ausfallwahrsch. =Lebensdauer50 % Ausfallwahrsch./(jn* jPA )
DIE SICHERHEIT DER DAUERFESTIGKEIT BEZÜGLICH AUSFALLWAHRSCHEINLICHKEIT
Für die Streuungen der Lebensdauerversuche (Wöhlerlinien) typischer Werkstoffe des Maschinenbaus liegen Erfahrungswerte vor. Haibach gibt Erfahrungswerte an (siehe folgende Tabelle).

Tabelle 1 Erfahrungswerte für die Streuung von Werkstoffdaten der Betriebsfestigkeit
Darin sind die logarithmischen Standardabweichungen sowohl in Lebensdauerrichtung (sN), also auch in Spannungsrichung (sσ) zusammengefasst. Mit der logarithmischen Normalverteilung können damit Sicherheiten bezüglich beliebiger Ausfallwahrscheinlichkeiten jPA berechnet werden.
Die Sicherheit definiert allgemein das Verhältnis aus dem Merkmalswert bei der gewünschten Ausfallwahrscheinlichkeit xPA zum Merkmalswert der Ausfallwahrscheinlichkeit von 50 % x: PA=50%, also dem Mittelwert:
jPA=xPA=50%/xPA =Mittelwert / x PA .
Für Schwingfestigkeitskennwerte wird die logarithmische Normalverteilung angenommen. In diesem Fall berechnet sich die Sicherheit in Abhängigkeit der Standardabweichung (z.B. aus obiger Tabelle) folgendermaßen:
jPA=(10)(u∙s)
Es ist u die Schranke der Normalverteilung für die gewünschte Ausfallwahrscheinlichkeit nach folgender Tabelle 2
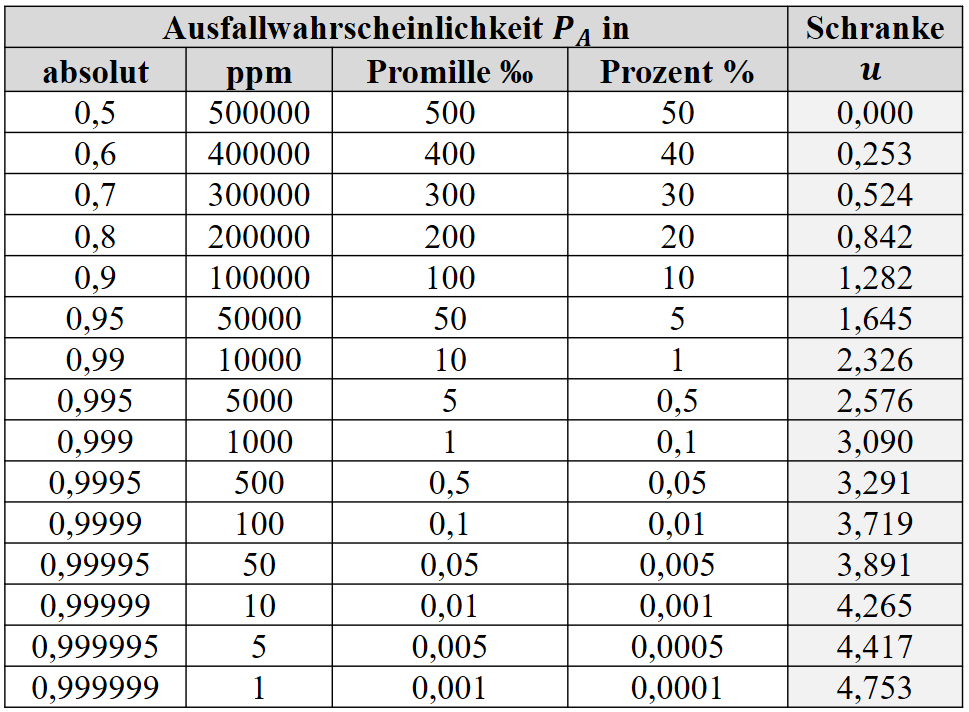
Tabelle 2: Schranken u der Normalverteilung
und s die Standardabweichung nach der ersten Tabelle.
Alternativ können die Sicherheitsfaktoren auch diesen Diagrammen entnommen werden:
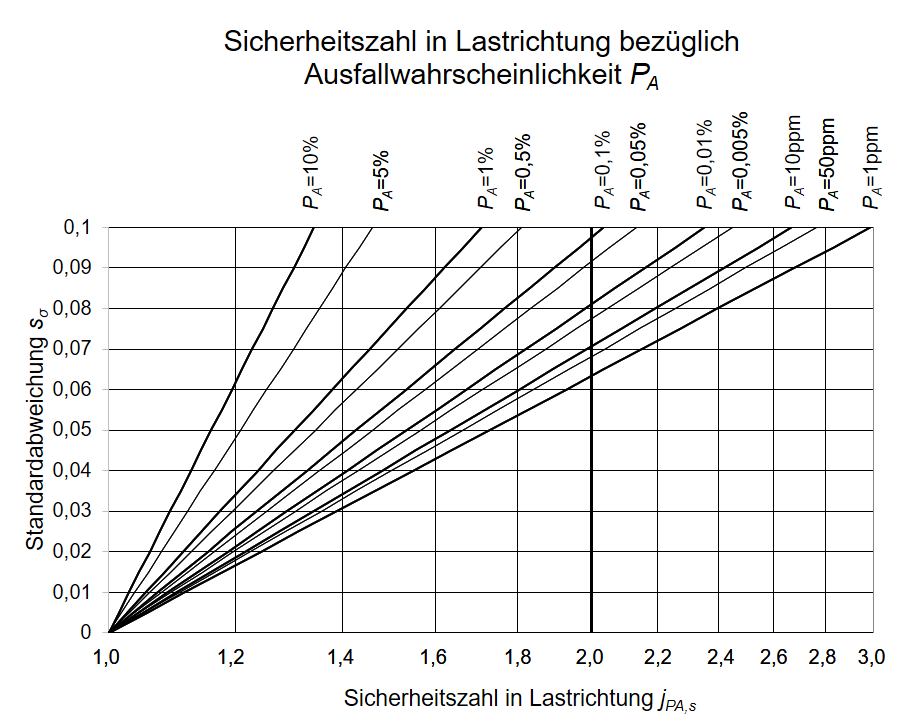
Abbildung 1: Sicherheit in Spannungsrichtung abhängig von der Streuung der Wöhlerlinien
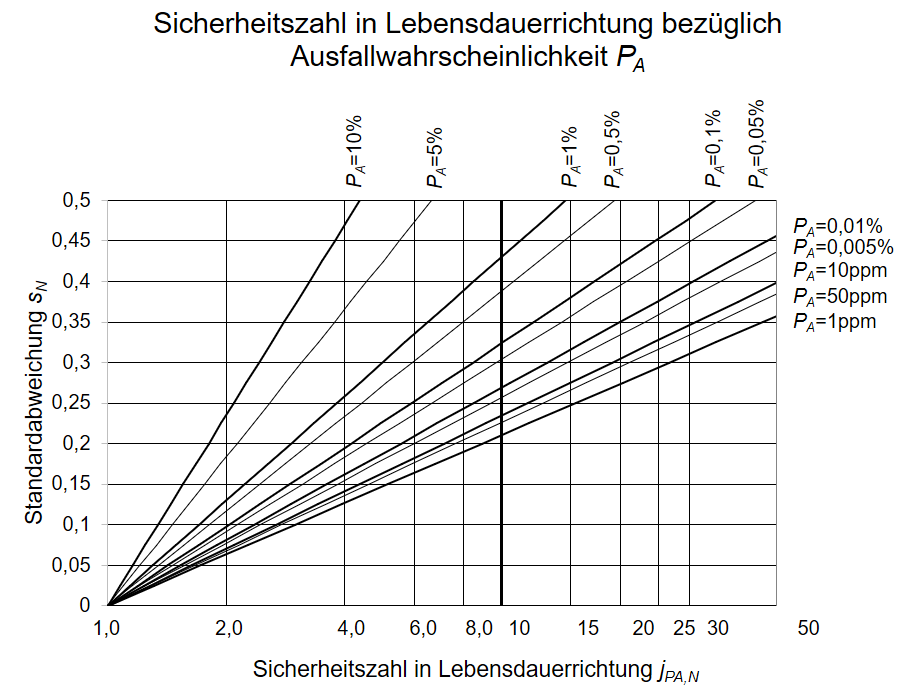
Abbildung 2: Sicherheit in Lebensdauerrichtung abhängig von der Streuung der Wöhlerlinie
Dazu ein Beispiel:
Die Ausfallwahrscheinlichkeit PA einer Getriebewelle aus Stahl soll nicht größer 1 ppm sein: PA < 1ppm. Die Belastung ist schwingend. Wir führen also einen Schwingfestigkeitsnachweis. Wie groß ist dann die Sicherheit zu wählen?
Lösung:
Wegen des Schwingfestigkeitsnachweises nehmen wir an, dass die Festigkeitskennwerte nach der logarithmischen Normalverteilung verteilt sind.
Wir nehmen außerdem an, dass die Welle spanabhebend bearbeitet wird und mäßige Kerben aufweist. Es ergeben sich nach der ersten Tabelle die logarithmischen Standardabweichungen
sN=0,197 in Lebensdauerrichtung
sσ=0,0392 in Spannungsrichtung
Zeichnerisch:
Aus den Diagrammen der Abbildung 1 und 2 werden für die Standardabweichungen und eine Ausfallwahrscheinlichkeit von PA = 1 ppm folgende Sicherheiten abgelesen:
jPA,N = f(PA;sN) ; mit sN=0,197; PA=1 ppm gilt jPA,N ≈ 9,0
jPA,σ = f(PA;sσ) ; mit sσ=0,0392; PA=1 ppm gilt jPA,σ ≈ 1,6
Rechnerisch:
Um eine Ausfallwahrscheinlichkeit von PA = 1ppm
jPA,N = 10u∙sN = 104,753∙0,197 = 8,64
jPA,σ = 10u∙sσ = 104,753∙0,0392 = 1,54
Wir erkennen, dass die Sicherheiten in Lebensdauerrichtung deutlich größer sind, als die in Spannungsrichtung. Dies liegt am relativ flachen Verlauf der Wöhlerlinie. Außerdem stellen wir fest, dass die typischen aus dem Maschinenbau bekannten Sicherheitsfaktoren von S=1,5…2 sehr gut mit den Sicherheiten für eine Ausfallwahrscheinlichkeit von 1ppm übereinstimmen, wenn in Spannungsrichtung bewertet wird. Dies ist der übliche Fall, da meist berechnete Spannungen (z.B. aus FEM) den ertragbaren Spannungen (z.B. Dauerfestigkeiten) gegenübergestellt werden.
Auf den Punkt
Sicherheiten können sowohl in Spannungsrichtung, als auch in Lebensdauerrichtung berechnet werden.
Sicherheiten in Lebensdauerrichtung sind immer größer als in Spannungsrichtung. Ursächlich sind die größeren Streuungen in Lebensdauerrichtung durch einen flachen Verlauf der Wöhlerlinie.
Zur Abschätzung von Streuungen von Werkstoffdaten für Stahl und Aluminium liegen Erfahrungswerte vor, so das Bauteile auch ohne eigene Versuche robust ausgelegt werden können.
Bevorstehende Events
Werkstoffkennwerte der Betriebsfestigkeit (für Simulation und Auslegung) einfach ermitteln und anwenden
- Schulung Werkstoffkennwerte der Betriebsfestigkeit - Präsenz Motel One Hbf Stuttgart - 09.-10.10.2024
9. Oktober 2024 - 10. Oktober 2024
9:30 am - 5:00 pm
Lernen Sie, wie Sie Versuche der Betriebsfestigkeit zur Ermittlung der Dauerfestigkeit oder von Wöhlerlinien planen und durchführen. Daneben lernen Sie diese Versuche statistisch einfach auszuwerten.
- Schulung Werkstoffkennwerte der Betriebsfestigkeit - Präsenz Motel One Hbf Stuttgart - 09.-10.10.2024
Seminar Grundlagen der Untersuchung von Werkstoffen und Schadensfällen
- Seminar zur Werkstoff- und Schadensanalyse - Präsenz - 10.-11.10.2024
10. Oktober 2024 - 11. Oktober 2024
9:30 am - 5:00 pm
Das Seminar beantwortet Ihnen im Wesentlichen zwei wichtige Fragen für Ihre Bauteilauslegung: 1) Ist das Material für meine Anforderungen verwendbar? und 2) Warum hat das Bauteil versagt? Ergänzt werden die vorgestellten Analysemethoden durch ausführliche Beispiele aus der Praxis.
- Seminar zur Werkstoff- und Schadensanalyse - Präsenz - 10.-11.10.2024
Seminar Betriebsfestigkeit von Schweißnähten mit / ohne FEM
- Seminar Betriebsfestigkeit von Schweißnähten mit/ohne FEM - Präsenz Motel One Hbf Stuttgart - 17.-18.10.2024
17. Oktober 2024 - 18. Oktober 2024
9:30 am - 5:30 pm
Sie wollen Ihre Bauteile möglichst leicht und sicher auslegen? Sie wollen die wichtigsten Richtlinien und Normen zur Berechnung der Betriebsfestigkeit von Schweißnähten kennenlernen und verstehen, wie sie diese für sich nutzen können? Suchen Sie einen Überblick über die Methoden zur Auslegung von Schweißnähten? Dann buchen Sie jetzt das Seminar Betriebsfestigkeit von Schweißnähten mit / ohne FEM.
- Seminar Betriebsfestigkeit von Schweißnähten mit/ohne FEM - Präsenz Motel One Hbf Stuttgart - 17.-18.10.2024
Anwendung der FKM Richtlinie mit FEM
- Schulung FKM Richtlinie - Präsenz NH Hotel Ludwigsburg - 24.-25.10.24
24. Oktober 2024 - 25. Oktober 2024
9:30 am - 5:30 pm
Finden Sie sich in der komplexen FKM Richtlinie zurecht und lernen diese anwenden. Sie verstehen, worauf es bei der Simulation mit FEM wirklich ankommt und kennen die Hintergründe der FKM Richtlinie. 18.04.-19.04.2024 : Motel One Germany Betriebs GmbH Motel One Stuttgart-Hauptbahnhof Kriegsbergstrasse 32 D-70174 Stuttgart 24.-25.10.2024 NH Hotel Ludwigsburg Pflugfelder Str. 36 71636 Ludwigsburg
- Schulung FKM Richtlinie - Präsenz NH Hotel Ludwigsburg - 24.-25.10.24
Einführung in die Betriebsfestigkeit von Kunststoffbauteilen
- Seminar Betriebsfestigkeit von Kunststoffbauteilen - Präsenz - 05.-06.11.24
5. November 2024 - 6. November 2024
9:30 am - 5:00 pm
Das Seminar zur Lebensdauerberechnung von faserverstärkten und unverstärkten Kunststoffen führt Sie schnell in die wichtigsten Konzepte (spannungs- und dehnungsbasiert) zur Berechnung von Kunststoffbauteilen mit der FEM ein. Sie erhalten Gestaltungsrichtlinien, lernen Bindenähte auszulegen und mit Anisotropien sowie Mehrachsigkeiten umzugehen.
- Seminar Betriebsfestigkeit von Kunststoffbauteilen - Präsenz - 05.-06.11.24
DoE: Design of Experiments - ein schneller Einstieg in die Anwendung
- Seminar DoE: Design of Experiments - schnelle Anwendung, Frühjahr 2024
7. November 2024 - 8. November 2024
9:00 am - 5:00 pm
Das Seminar DoE: Design of Experiments - ein schneller Einstieg in die Anwendung liefert Ihnen einen schnellen Start in die statistische Versuchsplanung. Damit können Sie Ihre Versuche sicher planen, begleiten und auswerten. Sie lernen, wie Sie mit minimalem Aufwand (Stichproben) die Einstellgrößen für die Inputfaktoren erhalten um optimale Größen für die Outputparameter zu erzielen. Gleichzeitig zeigen wir Ihnen die wichtigsten Grundlagen der Statistik für einen schnellen Einstieg. Und als besonderen Bonus erhält jeder Teilnehmer eine Schulungslizenz von Minitab®.
- Seminar DoE: Design of Experiments - schnelle Anwendung, Frühjahr 2024
Seminar Zuverlässigkeit
- Seminar technische Zuverlässigkeit - Präsenz- 07.-08.11.24
7. November 2024 - 8. November 2024
9:30 am - 5:30 pm
Nehmen Sie an diesem Seminar teil und lernen sie alles zum Thema Zuverlässigkeit: Bauteile robust auslegen und effizient erproben! Buchen Sie jetzt Ihren Platz.
- Seminar technische Zuverlässigkeit - Präsenz- 07.-08.11.24
Seminar Betriebsfestigkeit mit FEM
- Seminar Betriebsfestigkeit mit FEM - Präsenz - 07.-08.11.2024
7. November 2024 - 8. November 2024
9:30 am - 5:30 pm
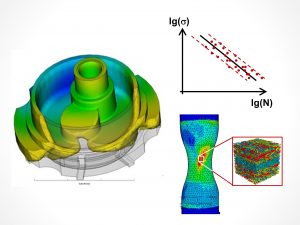
Das Seminar zur Betriebsfestigkeit mit FEM vermittelt eine kurze, auf die praktische Anwendung hin orientierte Einführung in die Betriebsfestigkeitsberechnung mit und ohne FEM. Z. B. rechnerische Abschätzung von Wöhlerlinien, Schadensakkumulation, Bewertung von FE-Ergebnissen oder die Festlegung geeigneter Sicherheitsfaktoren.
- Seminar Betriebsfestigkeit mit FEM - Präsenz - 07.-08.11.2024