Geeignete Sicherheitsfaktoren müssen die Streuungen der Werkstoffdaten (folgender Artikel) und den Umfang der Versuche (dieser Artikel) berücksichtigen. Ich zeige Ihnen eine einfache und schnelle Methode dazu, die jeder umsetzen kann.
Bei der Auslegung eines Bauteiles sind aufgrund der Streuungen Sicherheiten vorzuhalten um die gewünschten Ausfallwahrscheinlichkeiten garantieren zu können. Basiert die Bauteilauslegung auf Werkstoffkennwerten (z. B. Zugfestigkeit oder Wöhlerlinie), die durch eigene Versuche ermittelt wurden muss zusätzlich noch die Unsicherheit auf Grund der Stichprobenanzahl berücksichtigt werden.
Die Sicherheit setzt sich damit aus zwei Teilen zusammen:
Der Sicherheit bezüglich der Ausfallwahrscheinlichkeit jPA (wurde in diesem Artikel diskutiert: Link)
Die Sicherheit bezüglich des Stichprobenrisikos jn
Die gesamte Sicherheit j ist das Produkt dieser beiden Sicherheiten:
j= jPA∙jn.
Oder anders ausgedrückt gilt für die Lebensdauer bei einer beliebigen Ausfallwahrscheinlichkeit:
Lebendauerx % Ausfallwahrsch. =Lebensdauer50 % Ausfallwahrsch./(jn* jPA )
DIE SICHERHEIT BEZÜGLICH DER GRÖßE DER STICHPROBE
Üblicherweise kann ein Festigkeitsnachweis nach einer Richtlinie oder Norm erfolgen. Stellenweise ist dies allerdings nicht möglich. Insbesondere, wenn die eigenen Werkstoffe nicht von der Norm oder Richtlinie oder in zugängigen Datenbanken abgedeckt sind. Möglich ist das beispielsweise bei Verwendung neuer Werkstoffe (z.B. gesinterte Bauteile) oder untypischer Werkstoffe für den Maschinenbau (z.B. Eisenwerkstoffe wie Elektrobleche). In diesen Fällen erfolgt der Festigkeitsnachweis auf Basis eigener Versuche.
Die eigenen Versuche (z.B. Wöhlerlinien) sind dann als Stichprobe aufzufassen. Beim Rückschluss einer Stichprobe auf die Grundgesamtheit ist immer mit Unsicherheiten zu rechnen. Diese Unsicherheiten sind umso größer je kleiner die Stichprobe ist. Mit der Sicherheitszahl bezüglich des Stichprobenrisikos jn wird diese Unsicherheit berücksichtigt (siehe auch den Leitfaden für Betriebsfestigkeitsberechnung). Werden Daten mit hohen Stichprobenumfängen oder Daten aus Richtlinien / Normen verwendet kann dieser Sicherheitsfaktor entfallen.
Unter der Annahme, des einseitigen Vertrauensbereiches mit einer Aussagewahrscheinlichkeit von 90% wird die Sicherheitszahl bzgl. des Stichprobenrisikos jn berechnet. Sie ist abhängig von der Stichprobenanzahl n und der Standardabweichung s der Daten, unter der Annahme, dass die Daten nach der logarithmischen Normalverteilung verteilt sind:
jn=101,282∙s/√n.
Für die Streuungen der Lebensdauerversuche (Wöhlerlinien) typischer Werkstoffe des Maschinenbaus liegen Erfahrungswerte vor. Haibach gibt Erfahrungswerte an (siehe folgende Tabelle). Darin sind die logarithmischen Standardabweichungen sowohl in Lebensdauerrichtung (sN), also auch in Spannungsrichung (sσ) zusammengefasst.

Tabelle 1 Erfahrungswerte für die Streuung von Werkstoffdaten der Betriebsfestigkeit
Zur einfacheren Anwendung wird die Sicherheitszahl zusätzlich als Grafik dargestellt:
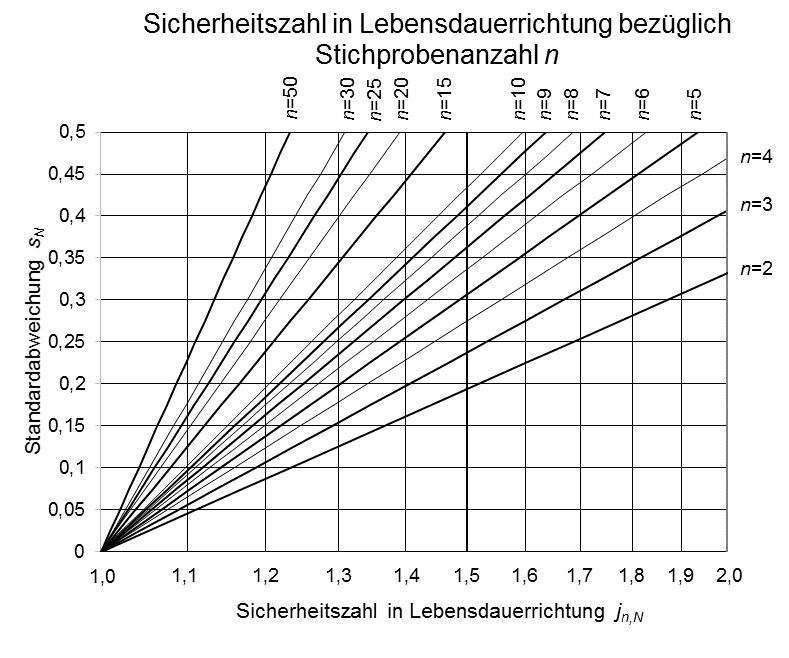
Sicherheit in Lebensdauerrichtung abhängig von der Stichprobe
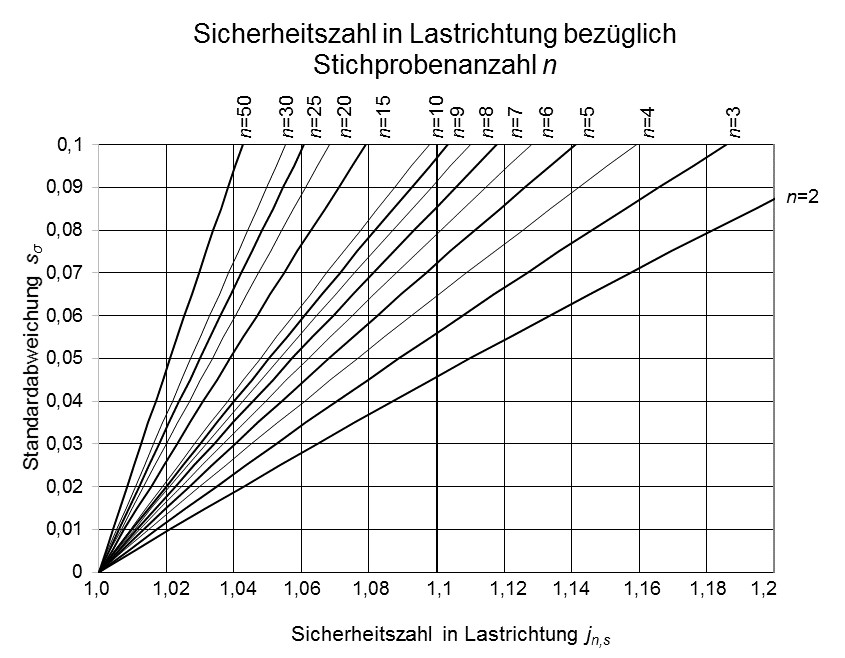
Sicherheit der Dauerfestigkeit in Abhängigkeit der Stichprobengröße
Auf den Punkt
Sicherheiten können sowohl in Spannungsrichtung, als auch in Lebensdauerrichtung berechnet werden.
Sicherheiten in Lebensdauerrichtung sind immer größer als in Spannungsrichtung. Ursächlich sind die größeren Streuungen in Lebensdauerrichtung durch einen flachen Verlauf der Wöhlerlinie.
Zur Abschätzung von Streuungen von Werkstoffdaten für Stahl und Aluminium liegen Erfahrungswerte vor, so das Bauteile auch ohne eigene Versuche robust ausgelegt werden können.
Es berechnet sich die Sicherheit abhängig von der Stichprobengröße n:
jn=101,282∙s/√n
und abhängig von der geforderten Ausfallwahrscheinlichkeit:
jPA=10u∙s
die gesamte Sicherheit ist das Produkt aus beiden Faktoren:
j= jPA∙jn.
In unserem Buch Statistik der Betriebsfestigkeit erfahren Sie, wie Sie die wichtigsten statistischen Methoden der Betriebsfestigkeit anwenden können:

