Raffung von Lastkollektiven: Wie Sie ihre Erprobungen in kürzester Zeit durchführen

Wollen Sie die Robustheit Ihrer Produkte in einer Erprobung nachweisen? Dann benötigen Sie Erprobungskollektive, welche dieselbe Schädigung hervorrufen, wie die Belastung im Feld (das Feldkollektiv). Da Feldkollektive oftmals sehr lang sind, werden Erprobungskollektive gerne gerafft. Wir zeigen Ihnen die gängigsten und wertvollsten Methoden.
In diesem Artikel lernen Sie
- 5 Methoden kennen um Ihr Erprobungskollektiv zu raffen
- Wie Sie aus einem Feldkollektiv ein Erprobungskollektiv ableiten
- Zwei unterschiedliche Kollektive bzgl. Ihrer Schädigung zu vergleichen
- Die Grenzen der Raffung von Kollektiven kennen
- an einem Beispiel die Raffung anwenden.
Inhalt
1 Motivation
Erprobungskollektive werden entweder vom Kunden in Lastenheften vorgegeben, oder müssen selber erarbeitet werden. Wichtig ist, dass die Erprobungskollektive immer denselben Schadensmechanismus (z.B. Schwingbruch) anregen, wie das Feldkollektiv.
Um eigene Erprobungskollektive abzuleiten, sind folgende Schritte notwendig:
- Ableitung eines Auslegungskollektivs aus Last-Zeitreihen mit Hilfe der Rainflow-Zählung und dessen Extrapolation.
- Raffung der Lastkollektive zu einem Erprobungskollektiv, um Erprobungszeiten zu sparen.
Generell kann eine Erprobung jetzt mit diesen Kollektiven durchgeführt werden. Jedoch sind diese oft relativ lang, so dass mit langen Erprobungszeiten gerechnet werden muss. Ein Auto beispielsweise hat eine Nutzungsdauer von etwa 15 Jahren. Das sind ca. 130 000 h. Betrieben wird das Auto jedoch „nur“ etwa 6 000 h. Testzeiten belaufen sich jedoch zum Teil auf nur wenige 100 h.
Um die Testzeit zu verkürzen, kann das Kollektiv gerafft und damit die Versuchszeit gekürzt werden. Das bedeutet, dass aus dem Feldkollektiv ein Erprobungskollektiv mit gleicher Schädigung aber kürzerer Versuchszeit (und damit höheren Lasten) abgeleitet wird.
2 Grundlagen
Raffung ist ein sehr wirkungsvolles Mittel, um Prüfzeiten zu reduzieren. Ziel der Raffung ist es, in kürzerer Prüfzeit dieselbe Schädigung wie im Feld zu erreichen. Dabei gibt es verschiedene Möglichkeiten die Prüfzeit gegenüber der Feldbelastung zu beschleunigen, z.B.
- Vernachlässigung nicht schädigender Lasten,
- Höhere Prüffrequenz als Belastungsfrequenz im Feld,
- Erhöhung der Prüflasten gegenüber den Feldlasten -> Raffung.
2.1 Raffungsfaktor
Bei den ersten beiden Punkten handelt es sich um keine Raffung im eigentlichen Sinne. Unter Raffung versteht man eine Prüfung bei der die Prüflasten gegenüber den Feldlasten erhöht sind, siehe linkes Bild folgender Abbildung. Im Englischen spricht man hier vom Accelerated Life Test (ALT). Dies führt zu einer Reduzierung der Lebensdauer des Bauteils und damit zu einer Verkürzung der Prüfzeit (siehe rechtes Bild folgender Abbildung). Wie stark sich die Prüfzeit gegenüber der Belastungsdauer im Feld reduzieren lässt, gibt der Raffungsfaktor AF an:
AF = tTest / tFeld = nTest / nFeld
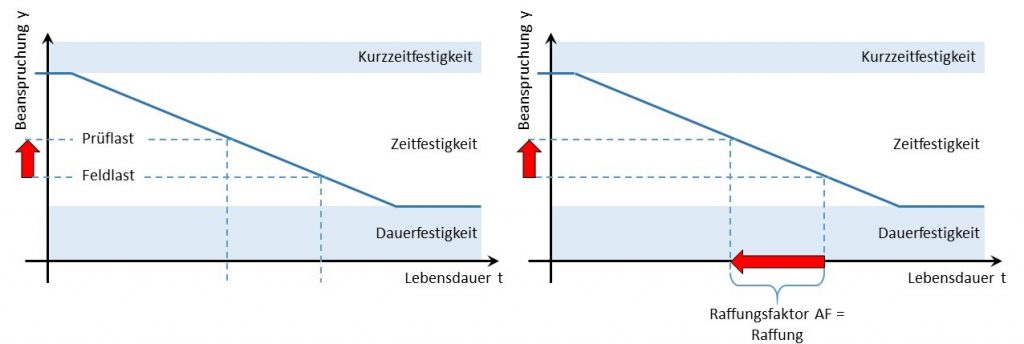
Erklärung des Raffungsfaktors und der Raffung am Beispiel der Wöhlerlinie
Um den Raffungsfaktor berechnen zu können, muss das Lebensdauermodell bekannt sein. Im Falle des Schwingbruchs ist dies die Wöhlerlinie des Bauteils. Dieses kann entweder experimentell oder auch rechnerisch abgeschätzt werden (z.B. mit Hilfe der FKM-Richtlinie). Eine Raffung ist immer nur für einen Schadensmechanismus möglich. D. h. vor der Prüfung muss klar sein, welcher Schadensmechanismus in der Prüfung angeregt und damit gerafft werden soll. Mögliche Schadensmechanismen sind z.B. Schwingbruch, Kriechen, statisches Versagen, Alterung, ….
Allgemein ist die Raffung aber sehr wirkungsvoll, da die Lebensdauermodelle üblicherweise sehr flach verlaufen, so dass eine geringe Erhöhung der Beanspruchung zu einer sehr deutlichen Reduzierung der Lebensdauer führen (siehe auch die Pfeile in der ersten Abbildung). Es sind durchaus Raffungen um den Faktor 1/AF = 10…50 möglich!
2.2 Grenzen der Raffung
Die Belastung während der Prüfung darf nicht so stark gegenüber der Feldbelastung erhöht werden, dass sich dabei der Schadensmechanismus ändert! Folgende Abbildung zeigt dies schematisch am Beispiel des Brütens von einem Ei. Im Bereich der Zeitfestigkeit kann das Ei bei höheren Temperaturen etwas schneller ausgebrütet werden. Sind die Temperaturen aber zu hoch, ändert sich der „Schadensmechanismus“ vom Brüten hin zum Kochen vom Ei. Dies ist der Bereich der Kurzzeitfestigkeit. Ist dagegen die Temperatur zu niedrig, wird sich gar nichts tun, wir befinden uns im Bereich der Dauerfestigkeit.
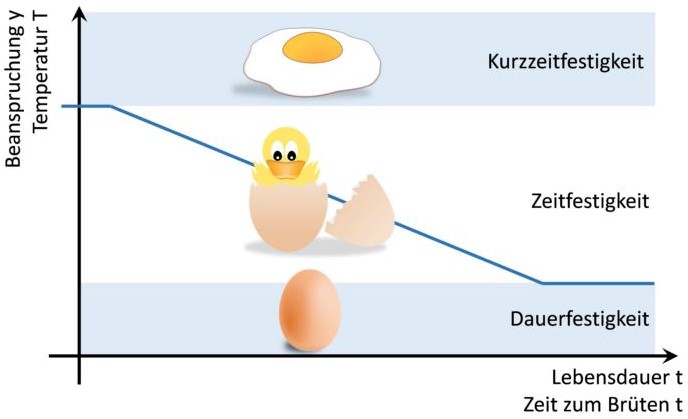
Grenzen und Risiken der Raffung
Im Falle der Betriebsfestigkeit kann im Bereich der Zeitfestigkeit sehr wirkungsvoll gerafft werden. Es ist dann darauf zu achten, dass weder die Kurzzeitfestigkeit oder die statische Festigkeit erreicht wird.
Lasten, die deutlich unterhalb der Dauerfestigkeit liegen können auch komplett gestrichen werden, da diese nicht mehr zur Schädigung beitragen (Omission).
3 Raffungsmöglichkeiten
Prinzipiell sind fünf Möglichkeiten der Verkürzung der Versuchszeit denkbar (siehe auch Haibach*) (in folgender Abbildung sind die Möglichkeiten 3) – 5) zusätzlich grafisch dargestellt):
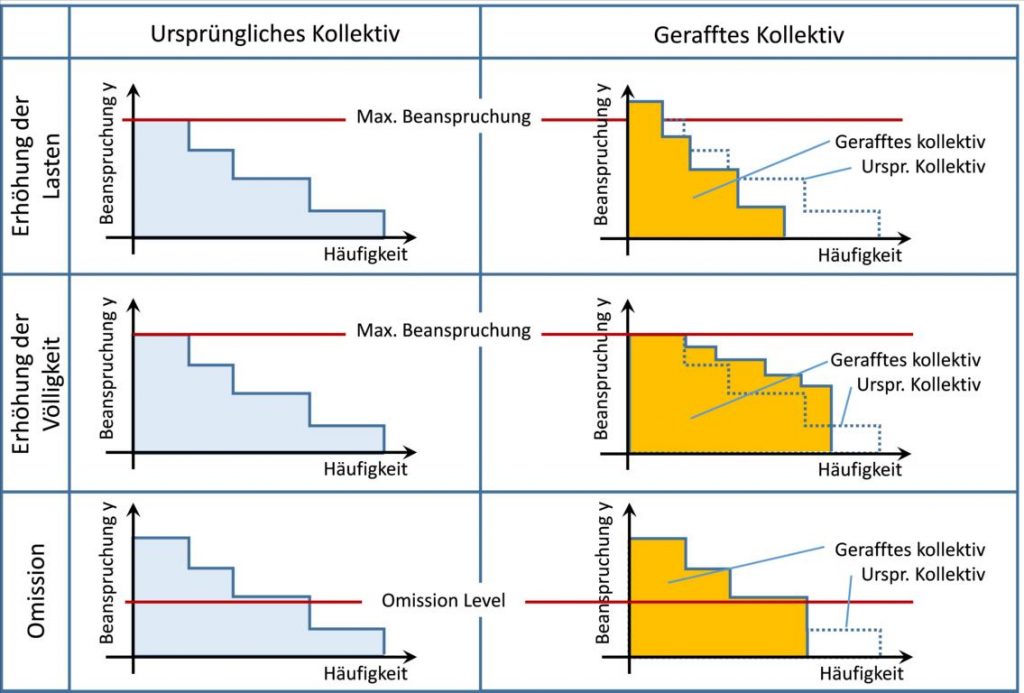
Möglichkeiten der Raffung (schematisch)
- Entfall von Beanspruchungspausen, die keinen Einfluss auf die Lebensdauer haben. Dies ist gut möglich, wenn kein Korrosiver Einfluss oder eine Schädigung durch höhere Temperaturen wie z.B. Kriechen auftritt.
- Schnellere Erprobung, indem die Prüffrequenz erhöht wird. Bei mechanischen Lasten können die Frequenzen für Bauteile aus Stahl auf max. 1000 Hz, bei Aluminium bis max. 100 Hz und Kunststoffe auf max. 10 Hz erhöht werden. Bei der Erhöhung der Frequenz von Temperaturhüben ist darauf zu achten, dass die Temperaturänderung im Bauteil Zeit benötigt, bis das Bauteil durchgewärmt ist. Diese Zeit begrenzt die maximale Frequenz.
- Höhere Lasten. Sofern diese höheren Lasten nicht einen neuen Schadensmechanismus anregen (vgl. dazu den Vergleich mit dem Ei) können die Lasten im Erprobungskollektiv gegenüber den Lasten des Feldkollektivs proportional überhöht werden (siehe oberes Bild in unterer Abbildung). Dazu wird ein schädigungsgleiches Erprobungskollektiv mit geringerer Häufigkeit berechnet. Für die Umrechnung wird die Schadensakkumulationshypothese nach Miner (oder kurz: Miner Regel) Im Falle der Korrosion kann z.B. der Salzgehalt oder die Temperatur angehoben werden. Bei der Schwingfestigkeit werden die Spannungsamplituden oder die Mittelspannungen erhöht. Neue Schadensmechanismen können bei der mechanischen Prüfung das Erreichen der statischen Festigkeit angeregt werden. Bei der Temperaturbelastung stellt das Erreichen der Glasübergangstemperatur oder der Schmelztemperatur eine solche Grenze dar. Zusätzlich muss sichergestellt werden, dass die Lasten auch im Prüffeld durch die Prüfstände aufgebracht werden können.
- Erhöhung der Völligkeit des Kollektivs, indem niedrige Laststufen in schädigungsgleiche höhere Laststufen mit geringerer Häufigkeit umgerechnet werden und gleichzeitig der Kollektivhöchstwert nicht geändert wird. Die Umrechnung geschieht mit Hilfe der Schadensakkumulationshypothese. Diese Vorgehensweise hat den Charme, dass der Kollektivhöchstwert gleichbleibt, wodurch die Anregung eines neuen Schadensmechanismus vermieden wird (siehe mittleres Bild in untenstehender Abbildung).
- Omission, d.h. niedrige, nicht schädigende Amplituden werden vernachlässigt und aus dem Erprobungskollektiv gestrichen (siehe Abbildung 12‑4 unteres Bild). Grenzen des Omission-Levels sind individuell festzulegen. Der Omission-Level wird im Bereich von 3…20% der Maximallast liegen. Das bedeutet, dass alle Lasten, die kleiner als das Omission-Level sind, aus dem Kollektiv gestrichen werden können.
Begründung: die untere Grenze von 3% begründet sich aus der Klassenbildung bei der Rainflow Zählung oder der Momentanwertzählung. Bei der Rainflow Zählung wurden alle Schwingspiele innerhalb einer Klasse vernachlässigt. Üblicherweise wurden 30...100 Klassen gewählt. Das bedeutet, dass alle Schwingspiele innerhalb von 1/30 tel (also etwa 3%) des Maximalwertes vernachlässigt wurden.
Die obere Grenze von 20% gilt für Betriebsfestigkeitsergebnisse bei geringen Mittelspannungen und sofern hohe Temperaturen und Korrosion ausgeschlossen werden können. So schlagen etwa Haibach* oder Radaj* vor, Spannungsamplituden von 20…50% der Dauerfestigkeit zu streichen.
Selbstverständlich ist auch eine Kombination aus den unter Punkt 1) - 5) genannten Methoden möglich. Mit diesen Methoden lassen sich Erprobungskollektive extrem stark raffen!
4 Berechnung
Die Bedingung für die Raffung mit höheren Lasten (siehe Punkte 3) und 4)) ist, dass die Schadenssumme D (also die Schädigung) beider Kollektive gleich ist. Es gilt somit, dass die Schadenssumme des Feldkollektives DFeld gleich der Schadenssumme des Prüfkollektives DTest ist:
DFeld = DTest
Die Schadenssumme D berechnet sich aus der Summe der Teilschädigungen di einer jeden Kollektivstufe
D = ∑ di.
Wobei sich die Teilschädigung di aus dem Verhältnis der wirkenden Zyklenzahl ni zur ertragbaren Zyklenzahl Ni berechnet:
di = ni / Ni.
Einsetzen der obigen Gleichungen ineinander liefert folgenden Zusammenhang:
DFeld = DTest
∑ di,Feld = ∑ di,Test
∑ ni,Feld / Ni,Feld = ∑ ni,Test / Ni,Test
Dabei kann die Anzahl an Kollektivstufen zwischen beiden Kollektiven voneinander abweichen. Wichtig ist nur, dass beide Kollektive dieselbe Schädigung im Bauteil hervorrufen. Um die ertragbare Zyklenzahl N berechnen zu können, wird das Lebensdauermodell des Schadensmechanismus auf den ausgelegt werden soll benötigt. Im Falle der Betriebsfestigkeit ist das die Wöhlerlinie. Die Berechnung von Wöhlerlinien für Kunststoffe ist hiermit möglich. Für die Berechnung der Wöhlerlinien von Metallen bietet sich die FKM Richtlinie an. Mit unserer Software zur FKM Richtlinie ist diese Berechnung sehr einfach möglich.
Bei der Auslegung von Erprobungskollektiven gibt es keine eindeutige Lösung! Das individuelle Prüfkollektiv muss durch Probieren gefunden werden.
Um die Verkürzung des Erprobungskollektives gegenüber dem Feldkollektiv angeben zu können wird der Raffungsfaktor AF analog obiger Definition berechnet.
AF = tTest / tFeld = nTest / nFeld = Umfang des Erprobungskollektivs / Umfang des Feldkollektivs
Darin ist tTest die Versuchsdauer bzw. der Umfang des Erprobungskollektives, und tFeld der Umfang des Auslegungskollektivs.
5 Praxistipps
Nicht immer ist das gesamte Lebensdauermodell bekannt! Was kann man dann tun? Zur Ableitung schädigungsgleicher Kollektive benötigt man streng genommen nicht das gesamte Lebensdauermodell (also nicht die gesamte Wöhlerlinie), sondern nur dessen Steigung m (wenn angenommen wird, dass es keine Dauerfestigkeit gibt). Im Falle der Wöhlerlinie ist dies der Neigungsexponent k.
Um ein schädigungsgleiches Kollektiv berechnen zu können, wird dann bei bekanntem Neigungsexponenten k einfach eine beliebige Dauerfestigkeit sD angenommen und damit das Erprobungskollektiv abgeleitet.
Dies ist sehr gut möglich, da die Neigungen von Wöhlerlinien für Metalle mit k = 3…5 und die Wöhlerlinienneigung von Kunststoffen mit k = 11..21 relativ gut bekannt sind.
Bei den Erprobungskollektiven muss außerdem darauf geachtet werden, dass diese am Prüfstand auch umsetzbar sind. In manchen Fällen müssen deshalb z.B. Minimalwerte oder Maximalwerte eingehalten werden.
Wird etwa ein Temperaturkollektiv berechnet, dann muss beim Erprobungskollektiv sichergestellt werden, dass der Ofen in dem die Erprobung durchgeführt wird, diese Temperaturen auch abbilden kann.
6 Beispiel
Die Raffung ist ein sehr mächtiges Werkzeug, wie das folgende Beispiel zeigt.
Die bleifreie Lotverbindung in einem Steuergerät wird im Betrieb durch wechselnde Temperaturhübe ΔT belastet. Ein typisches Lastkollektiv sieht folgendermaßen aus:
| i | ΔTi | ni |
| 1 | 150 K | 500 |
| 2 | 120 K | 8000 |
| 3 | 100 K | 17000 |
Bei Lotverbindungen unter der Belastung von Temperaturhüben gilt als Lebensdauermodell das
Coffin-Manson Modell:
ΔT = 10c ∙ N-1/b bzw. durch Umformen
N = 10c∙b ∙ ΔT -b.
Mit b = 1,8, c ist unbekannt.
Hinweis: b entspricht der Neigung der Wöhlerlinie und c entspricht dem Achsenabschnitt (also ganz grob der Dauerfestigkeit.
Das Kollektiv soll gerafft werden. Berechnen Sie die gerafften Kollektive für folgenden Fall: gesucht ist ein Prüfkollektiv, bei dem alle Stufen jeweils um 20% erhöht werden
Lösung:
Nach den Praxistipps wird nur die Steigung b für die Ableitung des Prüfkollektivs benötigt. Damit kann der Achsenabschnitt c beliebige Werte annehmen. Es wird c = 5 gewählt. Damit gilt als Lebensdauermodell:
N = 10c∙b ∙ ΔT -b = 105∙1,8 ∙ ΔT -1,8
Die Laststufen des gerafften Kollektivs ΔTi,Test werden auf ΔTi,Test = 1,2 ΔTi angehoben:
ΔT1,Test = 1,2 ∙150K = 180K,
ΔT2,Test = 1,2 ∙120K = 144K,
ΔT3,Test = 1,2 ∙100K = 120K.
Damit das Prüfkollektiv die gleiche Schädigung hervorruft wie im Feld, müssen die Zyklenzahlen reduziert werden. Dazu wird zuerst die Schädigung di jeder Stufe berechnet. Danach wird die Schädigung jeder Stufe gleich gelassen und die zum neuen Temperaturhub ΔTi,Test zugehörige Zyklenzahl ni,Test berechnet.
Die Schädigung di jeder Stufe wird folgendermaßen berechnet:
di = ni / Ni.
Die ertragbare Zyklenzahl Ni berechnet sich aus dem Lebensdauermodell. Die wirkende Zyklenzahl ni ergibt sich aus dem Kollektiv obiger Tabelle. Einsetzen des Lebensdauermodells liefert die Schädigung:
di = ni / Ni = ni / (105∙1,8 ∙ ΔTi -1,8)
Folgende Tabelle liefert die Schädigungen di und die ertragbaren Zyklenzahlen Ni je Stufe:
| I | ΔTi | ni | Ni | di |
| 1 | 150 K | 500 | 121070 | 0,0041 |
| 2 | 120 K | 8.000 | 180915 | 0,0442 |
| 3 | 100 K | 17.000 | 251189 | 0,0677 |
Die Berechnung der neuen Zyklenzahlen ni,Test für das geraffte Kollektiv erfolgt in der Art, dass in die Gleichung zur Berechnung der Schädigung die Zyklenzahl ni des Feldkollektivs durch die Zyklenzahlen ni,Test des gerafften Kollektivs ersetzt und die ertragbare Zyklenzahl des Feldkollektives Ni durch die ertragbare Zyklenzahl des gerafften Kollektivs Ni,Test ersetzt wird:
di,Test = ni,Test / Ni,Test.
dann wird diese Gleichung nach der Zyklenzahl des gerafften Kollektivs aufgelöst
ni,Test = di,Test ∙ Ni,Test.
und die ertragbare Zyklenzahl des gerafften Kollektivs Ni,Test wird jetzt noch durch die Gleichung des Lebensdauermodells ersetzt:
ni,Test = di,Test ∙ Ni,Test.= di,Test ∙ (105∙1,8 ∙ ΔTi -1,8).
Einsetzen der Temperaturhübe ΔT1,Test = 180K, ΔT2,Test = 144K, ΔT3,Test = 120K und der Schädigungen d1 = 0,0075, d2 = 0,096, d3 = 0,17 liefert anschließend die neuen Zyklen des gerafften Kollektivs. Die Ergebnisse zeigt folgende Tabelle:
| i | ΔTi,Test | Ni,Test | di | di,Test |
| 1 | 180 K | 87199 | 0,0041 | 360 |
| 2 | 144 K | 130301 | 0,0442 | 5762 |
| 3 | 120 K | 180915 | 0,0677 | 12244 |
Das Kollektiv wurde um den Faktor (∑ni/∑ni,Test ) = (500+8000+17000)/(360+5762+12244)=1,39 gerafft!
Analog kann auch bei Wöhlerlinien verfahren werden. Dazu können Sie einfach den Temperaturhub durch eine Spannungsamplitude und das Coffin Manson Modell rdurch die Wöhlerlinie ersetzen.
7 Auf den Punkt
- Raffungen sind ein sehr wirkungsvolles Mittel um Feldkollektive zu verkürzen und Erprobungszeiten zu minimieren.
- Beim Raffen muss sichergestellt werden, dass
- Der gleiche Schadensmechanismus im Feld wie in der Erprobung angeregt wird,
- Die Raffung nicht so hoch ist, dass neue Schadensmechanismen angeregt werden,
- Geraffte Kollektive dieselbe Schädigung wie die Feldkollektive haben,
- Prüfstände auch die gerafften Lasten aufbringen können.
- Es gibt prinzipiell fünf Möglichkeiten zu Raffen:
- Entfall von Beanspruchungspausen,
- Schnellere Erprobung,
- Höhere Lasten,
- Erhöhung der Völligkeitdes Kollektivs,
- Omission (streichen niedriger, nichtschädigender Lasten).
- Durch eine geschickte Kombination all dieser Möglichkeiten lassen sich Prüfzeiten gegenüber den Nutzungsdauern dramatisch reduzieren.
- Der Raffungsfaktor AF gibt an, wie stark die Raffung war.
- Als wichtigstes Werkzeug zur Berechnung der Raffung wird die Schadensakkumulation genutzt.
- Um Kollektive zu Raffen wird nur die Steigung des Lebensdauermodells benötigt. Im Falle der Wöhlerlinie ist dies die gut bekannte Neigung k.
Weiterführende Informationen zur Schadensakkumulation, FKM Richtlinie und Wöhlerkurven
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Betriebsfestigkeit mit FEM
Das Seminar zur Betriebsfestigkeit gibt Ihnen einen guten Überblick über die Methoden der Betriebsfestigkeit und der FEM. Hier lernen Sie
✓ alle wichtigen Methoden kennen, um Ihre Bauteile robust auf die Betriebsfestigkeit auszulegen.
✓ Schweißverbindungen auszulegen.
✓ verstehen, welche Faktoren die Lebensdauer Ihrer Bauteile besonders stark beeinflussen.
✓ Grundlagen der Finite-Elemente-Ergebnisse (FEM) kennen, anzuwenden und zu interpretieren.
✓ Lastkollektive mit Hilfe der Rainflowzählung zu ermitteln.
✓ eine Wöhlerlinie für Ihre Bauteile rechnerisch abzuschätzen.
✓ Bauteillebensdauern mittels Schadensakkumulation zu berechnen.
✓ Dauerschwingfestigkeitsnachweise zu führen.
✓ die modernen Regelwerke wie die FKM Richtlinie zur Betriebsfestigkeitsbewertung kennen.
Seminare zur FKM Richtlinie:
Haben Sie Interesse an einer schnellen Anwendung und einem einfachen Einstieg in die komplexe FKM Richtlinie? Dann ist unsere Schulung zur FKM Richtlinie für Sie richtig.
Diese ist genau richtig für Sie, wenn Sie
✓ die FKM Richtlinie schnell anwenden möchten.
✓ Ihre FEM Ergebnisse bewerten wollen.
✓ die Hintergründe der FKM Richtlinie verstehen und üben wollen.
Weiterführende Literatur
 Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses führt Sie schnell und verständlich in die Versuche und die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auslegung Ihrer Bauteile auf die Dauerfestigkeit oder Betriebsfestigkeit. Sie können dann einfach Wöhlerlinien für Ihre Bauteile berechnen.
Hilfreiche Software:

Wir haben basierend auf unserer jahrelangen Erfahrung, der Mitarbeit in den Forschungsgremien zur FKM Richtlinie und dem praktischen Arbeiten mit der Richtlinie FKMmadeEASY- die Online - Software zur FKM Richtlinie entwickelt. Wir haben dabei speziell darauf geachtet, dass diese Software
✓ einfachst möglich bedienbar
✓ gut dokumentiert und nachvollziehbar sowie
✓ optisch ansprechend ist (es soll ja auch Spaß machen).
Überzeugen Sie sich selbst davon anhand der Testversion von FKMmadeEASY - die Online-Software zur FKM Richtlinie
Der Autor:
Bildernachweis
Photo by Marc-Olivier Jodoin on Unsplash
