
Wöhlerlinien von Kunststoffen - ganz bequem berechnen!
Werkstoffdaten für einen Festigkeitsnachweis sind immer schwierig zu bekommen. Wir zeigen Ihnen wie Sie einfach eine Wöhlerlinie oder Dauerfestigkeit für Kunststoffe (Thermoplaste) berechnen können.
In diesem Artikel lernen Sie,
- Wie Sie die Dauerfestigkeit von thermoplastischen Kunststoffen und
- wie Sie eine Wöhlerlinie für thermoplastische Kunststoffe berechnen können.
Inhalt
1 Hintergrund
Das Feld der Kunststoffe ist weit. Grundsätzlich unterscheidet man bei einem Festigkeitsnachweis und dem mechanischen Verhalten zwischen
- Thermoplasten,
- kurzfaserverstärkten Thermoplasten,
- Elastomeren und
- Duroplasten.
Der Fokus in diesem Artikel liegt auf den Thermoplasten, denn die meisten Kunststoffe die wir benutzen sind Thermoplaste.
Thermoplaste sind dadurch gekennzeichnet, dass Sie bei einer bestimmten Temperatur (thermos = warm) formbar (= plastisch) sind. Dieser Zustand ist reversibel. Das bedeutet, dass der Werkstoff durch weiteres Abkühlen und Erwärmen erneut verformt werden kann.
2 Schadensmechanismen
Die typischen Schadensmechanismen von thermoplastischen Kunststoffen ähnelnd ebenfalls denen der Metalle.
- Statisches Versagen: bei hohen einmaligen Lasten kommt es zu unzulässig hohen plastischen Verformungen oder zum Bruch des Bauteils.
- Kriechen: Bei hohen Temperaturen und gleichzeitig wirkenden mechanischen Lasten kann sich der Werkstoff mit der Zeit bleibend verformen.
- Relaxation: Bei hohen Temperaturen und gleichzeitig wirkenden Dehnungen wird die Festigkeit über der Zeit abnehmen, der Werkstoff relaxiert.
- Schwingbruch: werden Lasten wechselnd (schwingend) aufgebracht, dann kommt es zur Ermüdung des Werkstoffes.
Aber Achtung! Im Gegensatz zu Metallen sind Kunststoffe sehr sensibel bezüglich der Temperatur und der Belastungsfrequenz! Denn mit zunehmender Frequenz der Belastung steigt die Eigenerwärmung im Kunststoff und damit sinkt die Festigkeit. Hohe Frequenzen können bereits bei wenigen Hz liegen.
In diesem Artikel fokussieren wir uns auf das statische Versagen und den Schwingbruch. Die Phänomene Kriechen und Relaxation werden wir deshalb ignorieren.
3 Statische Festigkeitskennwerte von Thermoplasten
In ihrem Werkstoffverhalten ähneln Thermoplaste den Metallen. Die Werkstoffkennwerte für den statischen Festigkeitsnachweis werden im Zugversuch ermittelt. Die Eigenschaften hängen jedoch stark von
- dem Werkstoff,
- der Temperatur (je höher die Temperatur, umso geringer die Festigkeit),
- der Belastungsgeschwindigkeit (je höher die Belastungsgeschwindigkeit, umso höher die Festigkeit)
ab, weshalb diese in Normen (z. B. ISO 527) eindeutig geregelt sind. Wie bei Metallen werden für Thermoplaste ebenfalls Werkstoffe mit ausgeprägter Streckgrenze und Werkstoffe ohne ausgeprägte Streckgrenze unterschieden (siehe folgende schematische Abbildung).
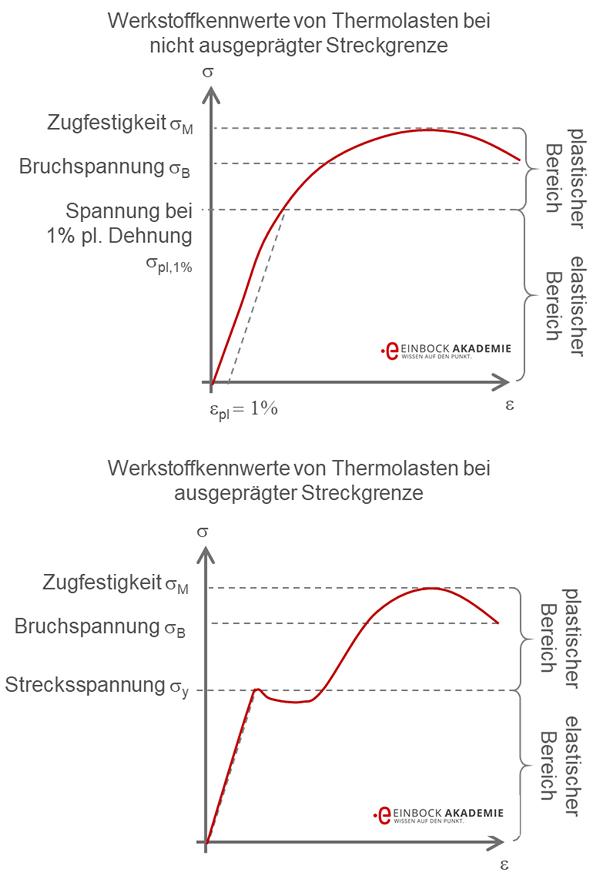
Werkstoffverhalten von Kunststoffen mit und ohne Streckgrenze
Wie in folgender Abbildung gezeigt, werden analog zu Metallen die Bereiche des
- Elastischen Werkstoffverhaltens und des
- Plastischen Werkstoffverhaltens unterschieden.
Der elastische Bereich endet bei der Streckgrenze σy (im Falle einer ausgeprägten Streckgrenze) oder bei der Spannung σpl,1% bei welcher 1 % plastische Dehnung auftritt (im Falle einer nicht ausgeprägten Streckgrenze). Der Bruch tritt bei der Bruchspannung σB ein und die die höchste ertragbare Spannung ist durch die Zugfestigkeit σM gekennzeichnet.
Der Festigkeitsnachweis von Thermoplasten kann entweder auf Basis von Dehnungen, oder auf Basis von Spannungen erfolgen. Da IngenieurInnen meistens den spannungsbasierten Festigkeitsnachweis von Metallen kennen, wird für Thermoplaste üblicherweise ebenfalls ein spannungsbasierter Nachweis durchgeführt!
3.1 Maßgebliche Kennwerte
Wie oben beschrieben sind die maßgeblichen Werkstoffkennwerte:
- Gegen Fließen:
- die Streckgrenze σy (im Falle einer ausgeprägten Streckgrenze) oder bei
- der Spannung σpl,1% (im Falle einer nicht ausgeprägten Streckgrenze)
- gegen Bruch:
- die Bruchspannung σB oder
- die Zugfestigkeit σM.
Für einen kompletten statischen Festigkeitsnachweis müssen noch weitere Einflüsse wie Temperaturen, Kriechen,... berücksichtigt werden.
3.2 Berechnung der statischen Festigkeit
Die statische Festigkeit berechnet sich in Abhängigkeit der Werkstoffgruppe (durch den Abminderungsfaktor AS) und der Streckgrenze σY wie folgt:
σstat = AS ∙ σY
Erfahrungswerte für den Abminderungsfaktor AS finden sich in folgender Tabelle:
| Abminderungsfaktor AS | ||
| Werkstoffgruppe | AS,min | AS,max |
| Teilkristalline, unverstärkte Thermoplaste | 0,8 | 1 |
| Amorphe, unverstärkte Thermoplaste | 0,65 | 0,8 |
| Teilkristalline, verstärkte Thermoplaste | 0,55 | 0,7 |
| Amorphe, verstärkte Thermoplaste | 0,55 | 0,7 |
4 Datenbanken für Kunststoffe
Werkstoffdaten können entweder in eigenen Versuchen ermittelt, oder aber aus Datenbanken ausgewählt werden.
Hier finden Sie auch eine Auswahl an kostenlosen Werkstoffdaten für Kunststoffe.
5 Wöhlerlinien von Kunststoffen
Bei der Ermittlung von Wöhlerlinien werden drei Bereiche unterschieden (siehe folgende Abbildung):
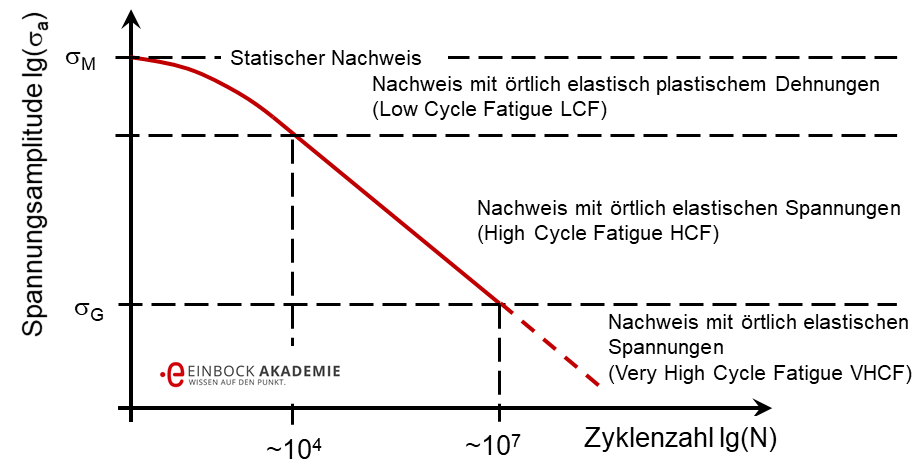
Wöhlerlinien von Kunststoffen (HCF, LCF und VHCF)
- Low Cycle Fatigue (LCF) für N < 104 Zyklen, in dem plastischen Dehnungen dominieren, und der Festigkeitsnachweis auf Basis von Dehnungen geführt wird
- High Cycle Fatigue (HCF) für N = 104 …107 Zyklen, in dem die elastischen Dehnungen dominieren und der Festigkeitsnachweis auf Basis von linear-(visko)elastischen Spannungen geführt wird,
- Very High Cycle Fatigue (VHCF) für N > 107 Mangels verfügbarer Daten wird angenommen, dass sich dieser analog zum High Cylce Fatigue Bereich verhält. Eine Dauerfestigkeit wird ausgeschlossen.
Sehr angenehm ist, dass der Festigkeitsnachweis für Thermoplaste im High Cylce Fatigue spannungsbasiert geführt wird. Deshalb gilt auch das Wöhlerlinienkonzept der Metalle! Zur Vertiefung der Themen empfiehlt sich z. B. das Buch zur FEM Berechnung von Kunststoffen* dessen Verfasser dieses Konzept zur Ermittlung von Wöhlerlinien für Kunststoffe erarbeitet haben.
5.1 Die Wöhlerlinien Gleichung
Das bedeutet, dass die mathematische Beschreibung der Wöhlerlinie für Kunststoffe im HCF Gebiet nach der Gleichung von Basqiun erfolgt:
σa = σG (Na/NG)-1/k
Mit
σa: Spannungsamplitude
σG: Grenzspannungsamplitude (Dauerfestigkeit)
Na: Zyklenzahl bei der Spannungsamplitude σa
NG: Grenzlastspielzahl (NG = 107)
k: Neigungsexponent
Zur Berechnung der Wöhlerlinie werden also drei Parameter benötigt:
- Die Grenzspannungsamplitude σG (Dauerfestigkeit)
- Die Grenzlastspielzahl NG
- Der Neigungsexponent k
5.2 Die Dauerfestigkeit σG von thermoplastischen Kunststoffen (Grenzspannungsamplitude)
Auf die Grenzspannungsamplitude σG von Kunststoffen wirken zahlreiche Einflüsse:
- Kerben (Stützwirkung ähnlich wie bei Stahl),
- Werkstoff,
- Temperatur,
- Feuchte,
- Mittelspannungen,
- Belastungsfrequenz,
- …
Für den vereinfachten Festigkeitsnachweis und die Berechnung der Dauerfestigkeit nach Stommel, Stojek und Korte* wird der Kerbeinfluss (also die Stützwirkung) ignoriert, da dieser positiv wirkt und das Ergebnis damit auf der sicheren Seite liegt.
Die Bauteildauerfestigkeit σG wird nach folgender Gleichung berechnet:
σG = KB ∙ KM ∙ σW
Wobei
σW die Wechselfestigkeit des Werkstoffes bei Mittelspannung σm = 0 (R = -1) ist. Diese kann wie folgt berechnet werden:
σW = AW ∙ K
Einsetzten in obige Gleichung liefert also:
σG = KM ∙ AW ∙ K
mit
σG: Bauteildauerfestigkeit
KM: der Mittelspannungsfaktor
AW: der Wechselfestigkeitsfaktor nachfolgender Tabelle
K: Statische Festigkeit aus dem Zugversuch (in Abhängigkeit der Temperatur), der Streckgrenze σY.
5.2.1 Die Berechnung des Wechselfestigkeitsfaktors AW
Mit Hilfe des Wechselfestigkeitsfaktors AW wird die Dauerfestigkeit bei rein wechselnder Last (R = -1) berechnet. Die folgende Tabelle gibt Erfahrungswerte an:
| Wechselfestigkeitsfaktors AW für N = 107 (R= -1) | ||
| Werkstoffgruppe | AW,min | AW,max |
| Teilkristalline, unverstärkte Thermoplaste | 0,2 | 0,3 |
| Amorphe, unverstärkte Thermoplaste | 0,17 | 0,20 |
| Teilkristalline, verstärkte Thermoplaste | 0,25 | 0,25 |
| Amorphe, verstärkte Thermoplaste | 0,17 | 0,17 |
5.2.2 Die Berechnung des Mittelspannungsfaktors KM
Der Mittelspannungsfaktor wird analog der Berechnung von Stählen in Anlehnung an die FKM Richtline* durchgeführt. In unserem Artikel zur Berechnung von Mittelspannungen finden sich dazu detaillierte Vorgehensweisen.
Einziger Unterschied ist, dass der Mittelspannungseinfluss anhand der Goodman Gerade im Haigh Diagramm dargestellt wird:
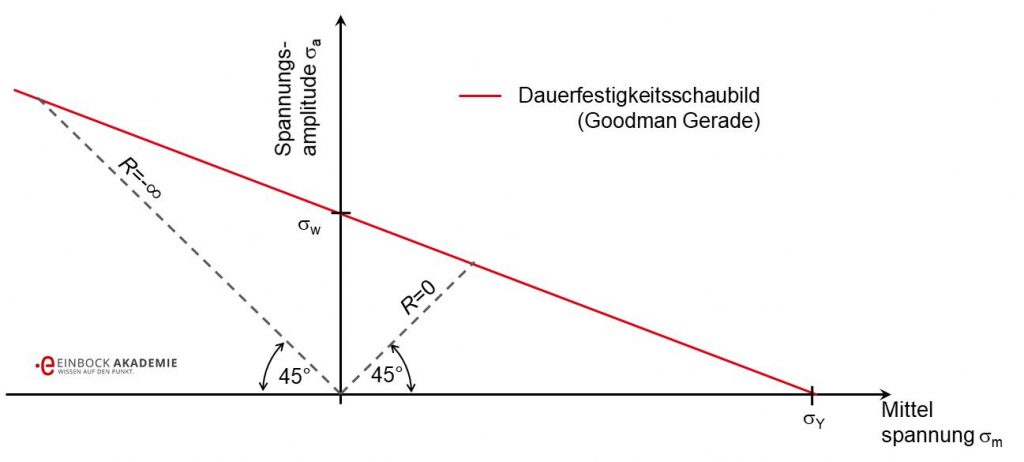
Dauerfestigkeitsschaubild von Kunststoffen (Goodman Gerade)
Wegen des rein linearen Verlaufs des Dauerfestigkeitsschaubildes wird die Mittelspannungsempfindlichkeit M in Abhängigkeit der Wechselfestigkeit σW und der Streckgrenze σY berechnet:
M = σW / σY.
Zur Berechnung des Mittelspannungsfaktors KM gelten die Gleichungen aus dem Artikel zur Berechnung von Mittelspannungen in Abhängigkeit des Überlastfalles. Für den häufigsten Überlastfall F2 (konstantes Spannungsverhältnis) gilt:
KM = 1/(1 + M ⋅ σm/σa)
mit der Mittelspannung σm und der Amplitudenspannung σa.
5.3 Die Grenzlastspielzahl NG von Wöhlerlinien für Thermoplaste
Kunststoffe besitzen im Gegensatz zu Stählen keine Dauerfestigkeit. Deshalb ist die Grenzlastspielzahl NG als eine Stützstelle der Wöhlerlinie anzusehen. Es wird gewählt:
NG = 107 Zyklen.
Denn: Die meisten Wöhlerversuche von Kunststoffen werden bis 107 Zyklen gefahren.
5.4 Der Neigungsexponent k von Kunststoff-Wöhlerlinien (Thermoplasten)
Als Erfahrungswerte für den Neigungsexponenten von Wöhlerlinen geben Stommel, Stojek und Korte in ihrem Buch zur FEM Berechnung von Kunststoffen* folgende Werte an:
| Neigungsexponenten k | ||
| Werkstoffgruppe | kmin | kmax |
| Teilkristalline, unverstärkte Thermoplaste | 11,63 | 13,39 |
| Amorphe, unverstärkte Thermoplaste | 11,63 | 12,02 |
| Teilkristalline, verstärkte Thermoplaste | 15,65 | 20,44 |
| Amorphe, verstärkte Thermoplaste | 11,39 | 13,73 |
Größere Neigungsexponenten führen zu flacheren Wöhlerlinien und damit zu konservativen Ergebnissen.
Streng genommen wird der Neigungsexponent nicht angenommen, sondern zeichnerisch ermittelt, siehe auch folgende Abbildung.
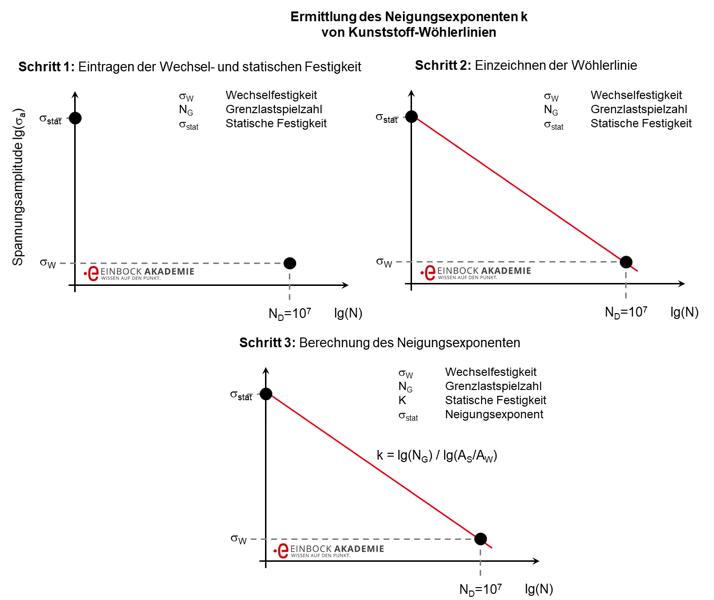
Zeichnerische Ermittlung der Wöhlerlinien-Neigung bei Kunststoffen
Schritt 1:
Dazu wird die statische Festigkeit σstat bei N = 1 und die Wechselfestigkeit σw bei N = NG = 107 eingezeichnet.
Schritt 2:
Anschließend werden die beiden Punkte miteinander verbunden.
Schritt 3:
Jetzt kann die Neigung durch Einsetzen der Punkte in die Wöhlerliniengleichung und Auflösen nach dem Neigungsexponenten k berechnet werden:
k = lg(NG) / lg(AS/AW).
6 Auf den Punkt
- Für thermoplastische Kunststoffe können Wöhlerlinien nach dem HCF Konzept analog zu Metallen als Gerade im doppellogarithmischen Netz beschrieben werden.
- Eine Dauerfestigkeit liegt für Kunststoffe nicht vor!
- Mit steigender Belastungsfrequenz bei schwingenden Lasten nimmt auch die Eigenerwärmung im Kunststoff zu. Deshalb wird bei hohen Frequenzen die Festigkeit absinken. Möglich ist dies bereits bei Frequenzen von wenigen Hz.
- Die Grenzlastspielzahl liegt üblicherweise bei NG = 107
- Als Neigungsexponenten werden konservativ k = 11,39 … 20,44 in Abhängigkeit der Werkstoffgruppe angegeben.
- Die „Dauerfestigkeit“ σG des Bauteils berechnet sich in Abhängigkeit der Statischen Festigkeit, und der Mittelspannung. Sie liegt ungefähr um den Faktor 0,17…0,30 geringer als die statische Festigkeit.
Weiterführende Informationen zur FKM Richtlinie und Wöhlerkurven
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Betriebsfestigkeit von Kunststoffbauteilen
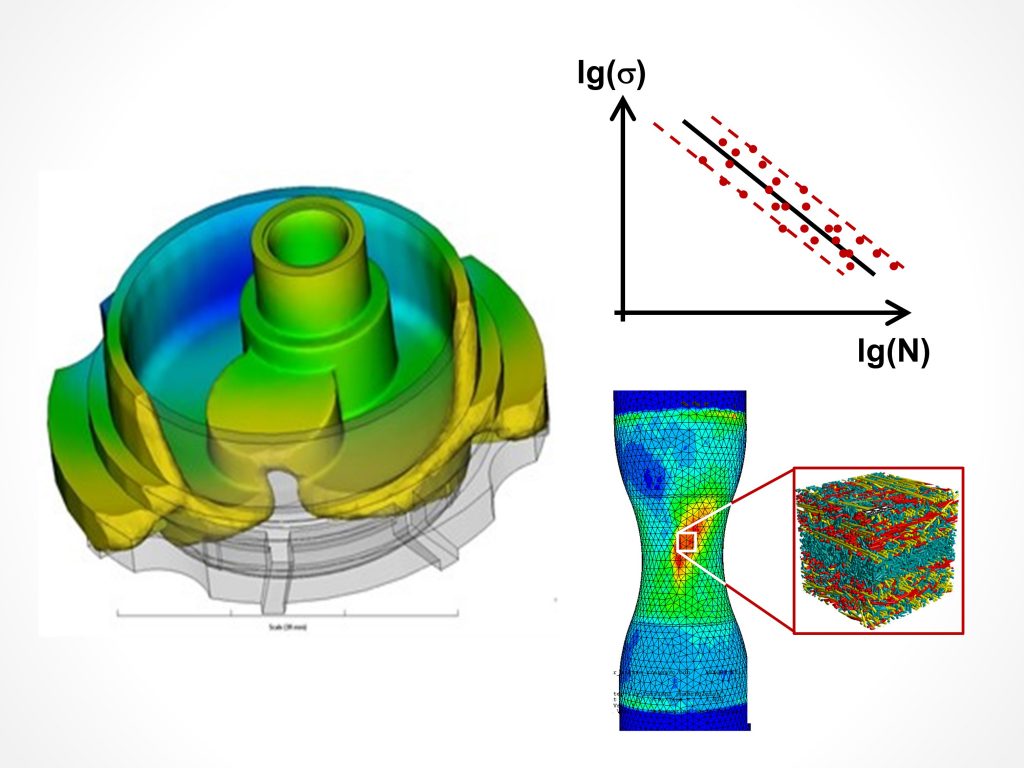
In diesem 2-tägigen Seminar erhalten Sie einen guten Überblick über die Methoden der Betriebsfestigkeit und der FEM mit speziellem Fokus auf Kunststoffbauteile und Sie lernen
- faserverstärkte und unverstärkte Kunststoffe bewerten,
mit der FEM Ihre Bauteile zu berechnen,
die wichtigsten Konzepte für die Simulation von Kunststoffen (auf Basis von Spannungen und Dehnungen) kennen,
Wöhlerlinien statistisch auszuwerten, - verstehen, welche Einflüsse die Lebensdauer bestimmen,
- alle wichtigen Konzepte für Thermoplaste kennen,
- die wichtigsten Schadensmechanismen von Kunststoff-Bauteilen kennen,
- Lastkollektive mit Hilfe der Rainflowzählung zu ermitteln und die Schadensakkumulation anzuwenden,
- Bindenähte im Spritzguss sowie Kunststoffschweißnähte zu bewerten,
- Kriechen, Alterung, thermo-mechanische Ermüdung kennen,
- einen Einblick in die Ermüdung von Elastomeren und Klebverbindungen.
Seminare zur FKM Richtlinie:
Haben Sie Interesse an einer schnellen Anwendung und einem einfachen Einstieg in die komplexe FKM Richtlinie? Dann ist unsere Schulung zur FKM Richtlinie für Sie richtig.
Diese ist genau richtig für Sie, wenn Sie
- die FKM Richtlinie schnell anwenden möchten.
- Ihre FEM Ergebnisse bewerten wollen.
- die Hintergründe der FKM Richtlinie verstehen und üben wollen.
Weiterführende Literatur
 Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses führt Sie schnell und verständlich in die Versuche und die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auslegung Ihrer Bauteile auf die Dauerfestigkeit oder Betriebsfestigkeit. Sie können dann einfach Wöhlerlinien für Ihre Bauteile berechnen.

Mein Vater hat Kunststofftechnik studiert. Deswegen kommen mir her einige Wörter auch bekannt vor. Kunststofftechnik ist immer noch ein angefragt Markt.
Hallo Jim,
danke für die netten Worte.
schöne Grüße
Stefan Einbock
Guten Tag,
ich habe eine Frage. Es geht in die Thematik strukturelle Integrität von FVK (GFK)
Im Bereich der Resonanz erfasse ich aus der gedämpften Schwingung in der Abklingkurve über das log. Dekrement die Dämpfung (fortlaufend). Ich möchte gern eine qualitative Aussage zum Thema
miner rule tätigen. Mir fehlt der Übergang Dämpfungsänderung zum Schwingverhalten (Amplitude)
Haben Sie eine Idee
Gruß
71f@web.de
Die kurze Antwort ist: ja 😉
Die lange Antwort ist:
Das logarithmische Dekrement D ist wie folgt definiert:
D = ln (x(t) / x(t+Td))
mit der Auslenkung x, dem Zeitpuntk t und der Schwingungsdauer Td
Der Faktor x(t) / x(t+Td) ist das Verhältnis
der Auslenkung (Amplitude) zum Zeitpunkt t (x(t)) zu
der Auslenkung (Amplitude) zum Zeitpunkt t+Td (x(t+Td)). Also der Amplitude nach genau einer Schwingung!
Wenn Sie jetzt die erste Amplitude kennen, dann können Sie alle anderen Amplituden so berechnen.
Beispiel:
Die erste Amplitude ist x(t1) = 5
Das logarithmische Dekrement ist D = 0,223
Das bedeutet, dass die zweite Amplitude bei x(t2) = x(t1+Td) = x(t1) / eD (Umformen obiger Gleichung) liegt: x(t2) = 5/e0,223 = 4.
Die dritte Amplitude liegt dann bei x(t3) = x(t2+Td) = x(t2) / eD = 4 / e0,223 = 3,2
Usw.
Alternativ können Sie auch das Bewegungsgesetz x(t) herleiten und dann ableiten und null setzten. Dann erhalten Sie alle Extremwerte (Amplituden).
Beispiele finden Sie etwa in dem Buch Technische Schwingungslehre von Knäbel, Jäger, Mastel aus dem Teubner Verlag* (Kapitel 5.2.1, Seite 87 ff).