Die plastische Formzahl nach der FKM Richtlinie einfach mit FEM Berechnen. Eine Schritt für Schritt Anleitung.

Inhalt

1. Grundlagen plastische Stützzahl und plastische Formzahl
2. Linearelastische FEM
   1. Prinzip
   2. Werkstoffgesetz
   3. Weitere Eingaben
3. Plastische FEM
   1. Prinzip
   2. Werkstoffgesetz
   3. Weitere Eingaben
4. Berechnung in Ansys
   1. Bauteil
   2. Werkstoffdaten
   3. Einstellungen zur plastischen Berechnung
   4. Netzfeinheit und Elemente
   5. Randbedingungen
   6. Berechnung
5. Berechnung der plastischen Formzahl mit FEM
   1. Berechnung der vollplastischen Traglast L_{vollplastisch}
   2. Berechnung der elastischen Grenzlast L_elastisch
   3. Berechnung der plastischen Formzahl K_p
6. Zusammenfassung
7. Ausblick

1 Grundlagen plastische Stützzahl und plastische Formzahl

Üblicherweise werden im Maschinenbau die Bauteile unter Annahme eines linearelastischen Werkstoffverhaltens berechnet. Das bedeutet, dass die Hook’sche Gerade als Werkstoffgesetz verwendet wird. Plastische Verformungen werden ignoriert.

1.1 Elastische Auslegung

Somit sind diese Ergebnisse nur für Spannungen unterhalb der Streckgrenze gültig. Wird die Belastung auf das Bauteil soweit gesteigert, dass die Spannungen (die Reaktion des Bauteils auf die Belastung) über der Streckgrenze liegen, ist das Ergebnis fehlerhaft. Die Berechneten Spannungen werden deutlich von den realen Spannungen abweichen.

Deshalb ist nach diesem Modell nur ein Festigkeitsnachweis gegenüber der Streckgrenze R_e möglich. Dennoch ist es üblich, die linearelastisch berechneten Spannungen auch mit der Zugfestigkeit R_m zu vergleichen. Warum darf man das tun?

Die Begründung liegt darin, dass die Annahme linearelastischen Werkstoffverhaltens zu konservativen Ergebnissen führt. Das bedeutet, dass die realen Spannungen (bei Annahme eines elastisch-plastischen Werkstoffverhaltens durch Verwendung der Spannungs-Dehnungs-Kurve des Werkstoffs) deutlich unterhalb der realen Spannungen liegen werden. Damit liegen die Ergebnisse auf der sicheren Seite.

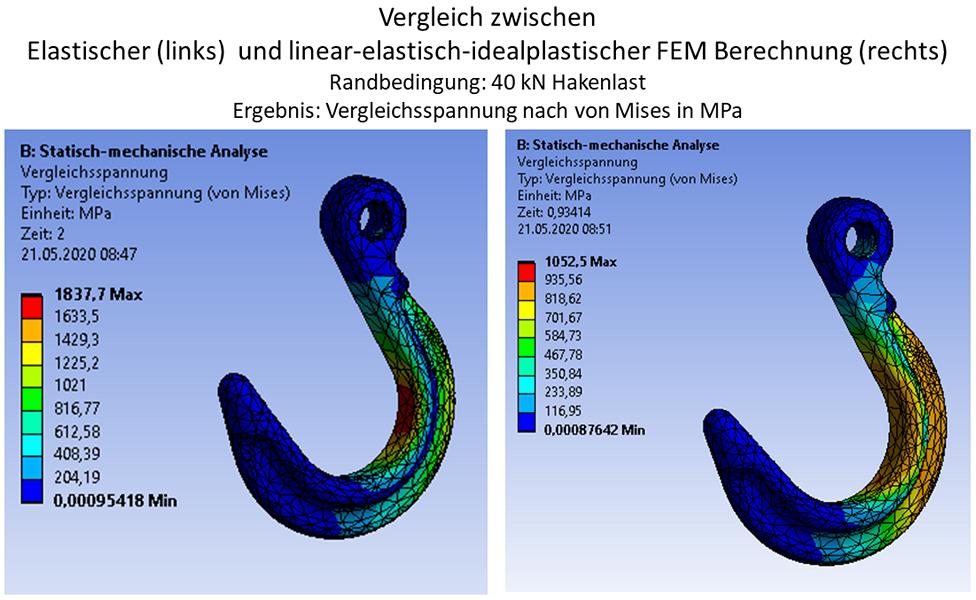
Vergleich der Ergebnisse einer elastischen und eine plastischen FEM Berechnung unter Annahme von linearelastisch-idealplastischem Werkstoffverhalten

Im Beispiel von obiger Abbildung ergeben sich für den Kranhaken bei 40 kN Last bei elastischer Berechnung eine Spannung von 1837 MPa und bei plastischer Berechnung unter Annahme des linearelastisch-idealplastischen Materialverhaltens etwa 900 MPa (also Spannungen in Größenordnung der Streckgrenze).

1.1 Die Chancen plastischer Auslegungen

Gleichzeitig bietet dies aber auch Chancen! Denn jetzt können wir bei Verwendung des realen Werkstoffverhaltens die Spannungen genauer berechnen und Tragreserven heben. Kurz zusammengefasst ist es bei

• duktilen Werkstoffen und
• gekerbten Bauteilen

möglich, lokal eng begrenzte plastische Dehnungen zuzulassen, wenn diese nicht zu

1. eine zulässige ertragbare Dehnung nicht überschreiten und
2. nicht zu einer Plastifizierung im gesamten Querschnitt des Bauteils führen

1.2 Die plastische Formzahl

Dazu haben wir in unserem letzten Artikel zur Neuber-Regel und der plastischen Stützzahl die plastischen Stützzahl n_pl nach der FKM Richtlinie kennengelernt. Kurz zusammengefasst besteht die plastische Stützzahl aus zwei Teilen, von denen das Kleinere maßgeblich ist:

n_pl = MIN([E · ε_ert  / R_e]^1/2; K_p)

1. Das Dehnungskriterium: sichert gegen die vom Material ertragbare Dehnung (e_ert) ab.
   ([E · ε_ert / R_e]^1/2, mit dem E-Modul E und der Streckgrenze R_e) und
2. Die Traglast, welche durch die plastische Formzahl K_p beschrieben wird:  und stellt sicher, dass nicht der gesamte Bauteilquerschnitt plastisch verformt ist
   (K_p = vollplastische Traglast (L_{vollplastisch}) / elastische Grenzlast (L_elastisch)). Die plastische Formzahl lässt sich analytisch nur für sehr einfache Geometrien berechnen. Deshalb wird dafür die FEM benötigt.

Das Dehnungskriterium kann bequem analytisch mit der Neuber-Regel berechnet werden. Wohingegen die Traglast K_p nur für sehr einfache Bauteile analytisch berechnet werden kann. Hierfür wird eine plastische FEM Rechnung benötigt.

Die plastische Formzahl ist definiert als das Verhältnis aus der Last bei welcher der Querschnitt vollplastisch ist (vollplastische Traglast L_{vollplastisch}) zur elastischen Grenzlast L_elastisch:

K_p = L_{vollplastisch} / L_elastisch.

L_elastisch ist die elastische Grenzlast. Das ist die Last, bei der an der höchst beanspruchten Stelle gerade die Streckgrenze Erreicht wird. L_{vollplastisch} ist die Last, bei der der gesamte Querschnitt plastisch verformt ist.

Vor allem für gekerbte Bauteile aus duktilen Werkstoffen mit niedriger Festigkeit ist häufig die Traglast das begrenzende Kriterium, weshalb sich hier eine genaue Berechnung mit FEM lohnen kann.

Deshalb schauen wir in den nächsten Schritten also auf die FEM Berechnung. Beginnen wollen wir mit der linearelastischen FEM und dann gehen wir weiter zur plastischen FEM.

2 Linearelastische FEM

Bei der Berechnung von Bauteilen mit der Finiten Elemente Methode (FEM) wird ein Bauteil in eine endliche Anzahl (eine finite Anzahl) kleiner Elemente eingeteilt. Für jedes dieser Elemente werden dann die gesuchten Größen (z. B. Spannungen oder Dehnungen) berechnet.

2.1 Prinzip

Bei einer linearelastischen FEM Berechnung wird angenommen, dass als Werkstoff linearelastisch verhält. Es gilt also als Werkstoffgesetz nur das die Hook’sche Gerade. Auf Grund der Linearität zwischen Kraft, Spannung und Dehnung ist diese Art der Simulation sehr einfach. Das FEM Programm wird bei den richtigen Eingaben immer gute Lösungen ausgeben.

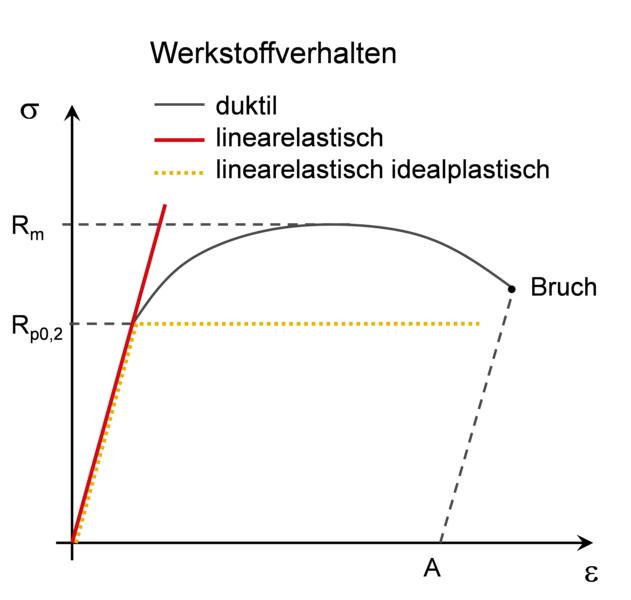
Vergleich der Werkstoffgesetze (duktil, linearelastisch und linearelastisch-idealplastisch)

2.2 Werkstoffgesetz

Für die Durchführung einer linearelastischen FEM Berechnung benötigt man verschiedene Werkstoffdaten. Paradoxerweise werden bei einer linearelastischen Berechnung von Spannungen KEINE Werkstoffdaten benötigt! Erst wenn Dehnungen berechnet werden sollen, wird das Werkstoffgesetz in Form der Hook’schen Gerade verwendet.

Warum ist das so?

Schauen wir uns dazu kurz die Gleichung zur Berechnung der Spannungen s an:

σ = F /A.

Hieraus wird ersichtlich, dass die Spannungen im Bauteil nur von der Kraft F (Belastung) und der Geometrie abhängen, nicht jedoch vom Werkstoffgesetz! Das heißt, dass geometrisch gleiche Bauteile aus Stahl und Kunststoff bei gleicher Belastung dieselben Spannungen sehen!

Im Gegensatz dazu, wird bei der Berechnung der Dehnungen ε jetzt das Werkstoffgesetz (der E-Modul E) benötigt:

ε = σ / E = F /A /E.

Hier zeigt sich, dass die Dehnungen ε neben der Spannung (also der Kraft und der Geometrie) auch vom Werkstoff abhängen. Geometrisch gleiche Bauteile aus unterschiedlichen Werkstoffen sehen jetzt bei gleicher Belastung wie erwartbar unterschiedliche Dehnungen.

Für die linearelastische FEM Berechnung wird somit nur der E-Modul und die Querkontraktionszahl als Werkstoffgesetz benötigt.

2.3 Weitere Eingaben

Außerdem muss noch auf eine ausreichend feine Vernetzung gesorgt werden.

Zusätzlich muss in einem FEM Programm immer auch die richtige Art der Simulation gewählt werden.

Bei ANSYS ist das z.B. die statisch-mechanische Analyse. Bei der kostenlosen, hoch professionellen FEM Software Salome-Meca ist dies „static mechanical analysis“.

3 Plastische FEM

Bei der plastischen FEM Berechnung ist keine direkte Lösung mehr möglich! Das bedeutet, dass die Lösung schrittweise (iterativ) erfolgen muss.

Deshalb dauern plastische FEM Berechnungen immer deutlich länger als elastische FEM Berechnungen. Gleichzeitig steigt bei der plastischen FEM Berechnung auch das Risiko, dass das FEM Programm keine Lösung findet (nicht konvergiert / abbricht).

3.1 Prinzip

Das Standardverfahren ist die Verschiebungsmethode. Nach dieser Methode sind die Verschiebungen die unbekannten Größen, welche berechnet werden. Bei den plastischen FEM Berechnungen nähert man sich durch mehrere FEM Berechnungen in kleinen Schritten der richtigen Lösungen (den richtigen Verschiebungen) an.

Dazu werden in einem ersten Schritt die Verschiebungen u₁ berechnet. Im zweiten Schritt wird die Last erhöht und ebenfalls wieder die Verschiebungen u₂ berechnet. Liegt jetzt der Unterschied zwischen beiden Verschiebungen Δu = u₁ – u₂ unterhalb eines Grenzwertes, wird die Lösung akzeptiert (die Berechnung ist konvergiert). Falls nein, wird die Last nochmals geändert.

Daraus resultiert im Vergleich zur linearen elastischen FEM Berechnung neben der längeren Rechenzeit manchmal ein Problem in Bezug auf die Konvergenz. D. h. die Software findet keine Lösung.

Ursächlich dafür können sein:

1. Ein sehr flacher Verlauf des Werkstoffgesetzes (der Spannungs-Dehnungs-Kurve). Den Worst Case stellt hier eine horizontale Spannungs-Dehnungs-Kurve dar. Diese kann bei einer linearelastisch-idealplastischen Berechnung wie im obersten Bild dargestellt vorkommen.
2. Simulationen, bei denen die Kraft als Belastung vorgegeben wird.

Dem kann auf einfache Art begegnet werden:

Zu 1: Es wird anstelle einer linearelastisch-idealplastischen Spannungs-Dehnungs-Kurve mit einem bilinearen Materialgesetz (erste Steigung: E-Modul, zweite Steigung: E/1000) gearbeitet. Dies ist analog dem Beispiel von der FKM-Richtlinie^*. Siehe dazu folgende Abbildung.

Zu 2: Anstelle einer Belastung durch eine Kraft, wird eine Belastung durch Wege / Verschiebungen vorgegeben.

3.2 Werkstoffgesetz

Im Fall der Berechnung der plastischen Formzahl und dort insbesondere der plastischen Formzahl K_p wird nach der FKM-Richtlinie^* immer ein linearelastisch-idealplastisches Werkstoffverhalten vorausgesetzt.

Wegen der besprochenen Probleme bei der Konvergenz der FEM Berechnungen bei Verwendung von linearelastisch-idealplastischem Werkstoffverhalten kann auch mit einem bilinearen Werkstoffverhalten gearbeitet werden. Für das Bilineare Werkstoffverhalten wird eine zweite Steigung E^* von einem tausendstel des E-Moduls empfohlen. Also E^* = E / 1000. Für Stahl wäre dies also E^* = 210 000 MPa / 1000 = 210 MPa. Gerne wird diese zweite Neigung auch als Tangentenmodul bezeichnet.

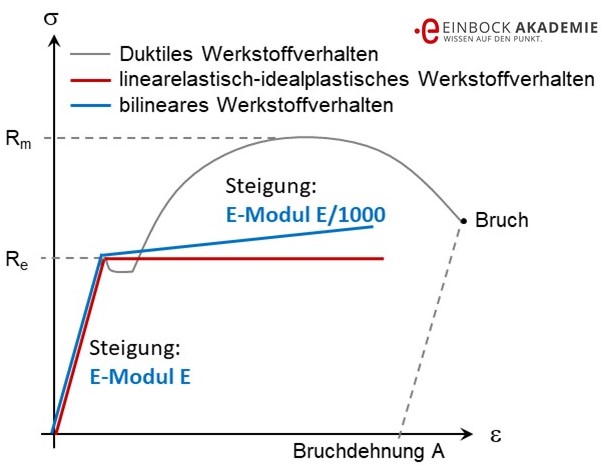
Modifizierung des linearelastisch-idealplastischen Werkstoffverhaltens für eine robuste plastische FEM Berechnung

Die dadurch entstehenden Fehler sind üblicherweise vernachlässigbar.

Wenn plastische Berechnungen in der FEM mit einem realen Werkstoffgesetz durchgeführt werden sollen, dann achten Sie darauf, die wahren Spannungen und Dehnungen und nicht die Ingenieurdehnungen sowie Ingenieurspannungen eingegeben werden.

3.3 Weitere Eingaben

Neben dem Werkstoffgesetz, der Geometrie und der Belastung muss bei plastischen FEM Berechnungen noch die Art der Verfestigung (isotropisch oder kinematisch) vorgegeben werden. Dabei handelt es sich um eine Angabe, wie sich der Werkstoff nach der Entlastung verhält.

Im Falle einer einmaligen Belastung (wie bei unseren statischen Berechnungen) liefern beide Verfahren identische Ergebnisse. Deshalb ist hier die Wahl beliebig.

4 Berechnung in ANSYS

Wie die Berechnung der plastischen Formzahl in ANSYS erfolgt, zeigen wir in diesem Kapitel anhand der Geometrie des Kranhakens.

4.1 Bauteil

Am Beispiel des Kranhakens wird die Berechnung der plastischen Formzahl vorgestellt. Der Kranhaken ist aus 42CrMo4. Die Geometrie des Kranhakens können Sie hier herunterladen.

Es wird angenommen, dass der Kranhaken aus dem Stahl 42CrMo4 mit R_m = 1100 MPa, R_e = 900 MPa und E = 211 400 MPa gefertigt wurde. Siehe dazu auch die folgende Abbildung.

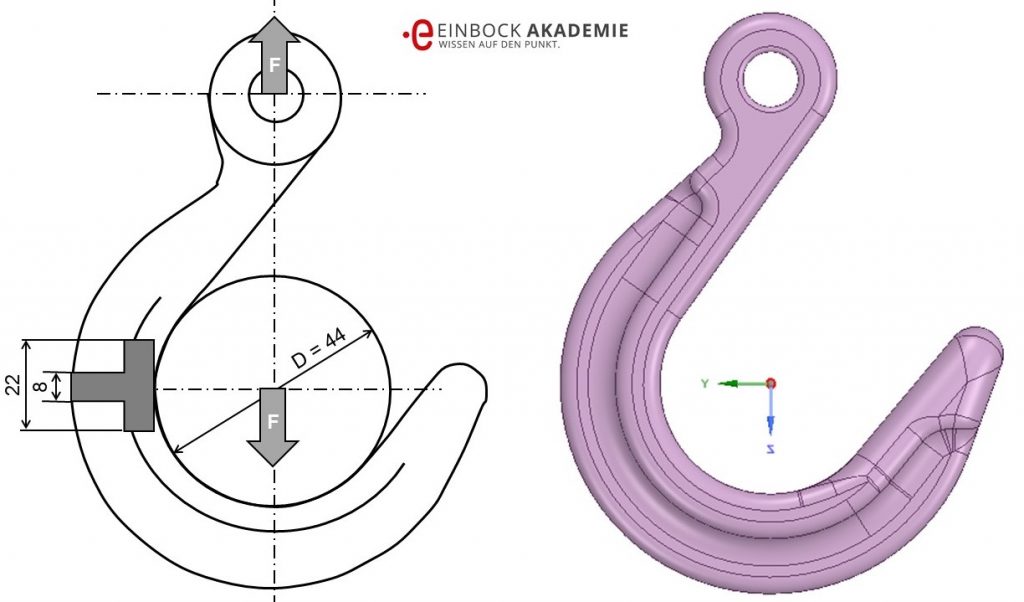
Kranhaken als Bauteil zur Berechnung der plastischen Formzahl

Belastet ist der Kranhaken durch eine zentrische Last F. Gesucht ist die plastische Formzahl K_p.

4.2 Werkstoffdaten

In AnsysWorkbench werden bei den technischen Daten im Bereich Plastizität die Werkstoffdaten eingegeben. Es wird ein bilineares isotropes Materialverhalten gewählt. Wichtig sind hier die folgenden Daten:

• E = 211 400 MPa
• R_e = 900 MPa
• Tangentenmodul E* = E / 1000 = 211,4 MPa

Die Zugfestigkeit wird nicht benötigt. Die Streckgrenze wird als Abknickpunkt benötigt. Der Tangentenmodul ist die zweite Neigung der Spannungs-Dehnungs-Kurve. Die folgende Abbildung zeigt das Werkstoffgesetz.

bilineares Werkstoffgesetz in ANSYS zur Berechnung der plastischen Sützzahl mit FEM

Hier finden Sie außerdem eine gute Quelle für Werkstoffdaten und Wöhlerlinien für Stahl und Aluminium.

4.3 Einstellungen zur plastischen Berechnung

Bei plastischen Berechnungen müssen immer zwei Vorgaben getroffen werden:

1. Die Anzahl der Lastschritte (also die Vorgabe, wie sich die Last über der Zeit ändert) und
2. Die Anzahl der Substeps je Lastschritt (also die Vorgabe, wie fein die Laststeigerung in jedem Lastschritt erfolgt).

Die Vorgabe erfolgt im Punkt „Analyseeinstellungen“, siehe dazu auch die folgende Abbildung.

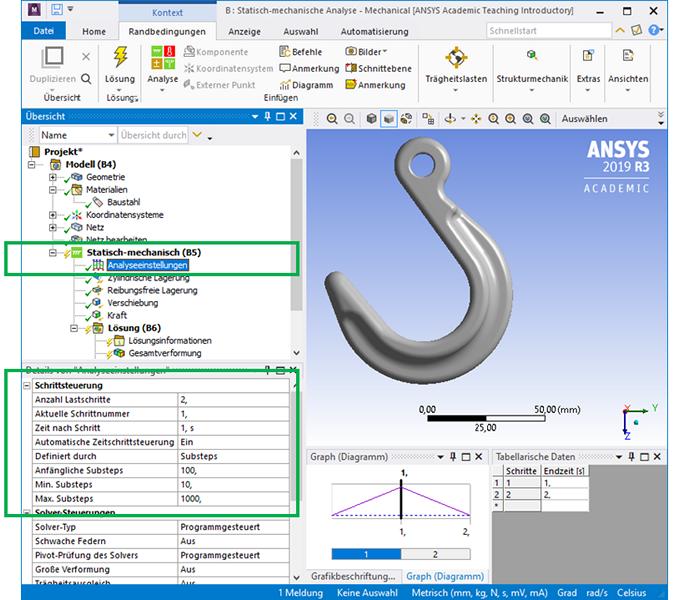
Einstellungen der Lastschritte in ANSYS zur plastischen FEM Berechnung

In unserem Beispiel wird die Berechnung mit zwei Lastschritten durchgeführt. Das sind die Schritte:

1. Belastung des Kranhakens mit der Hakenlast und
2. Entlastung des Kranhakens um zu überprüfen, ob es zu plastischen Verformungen gekommen ist.

Bei der Vorgabe der Substeps wird ausgewählt, in welchen Schritten die Last erhöht wird. Je höher die Anzahl an Substeps ist, umso feiner wird die Last gesteigert. Dies führt dann dazu, dass auch große plastische Verformungen gut abgebildet werden. Gleichzeitig steigt allerdings die Rechenzeit.

Üblicherweise kann mit der „automatischen Zeitschrittsteuerung“ gearbeitet werden. Dazu wird diese auf „Ein“ gesetzt.  Dies führt zu einer hohen Robustheit der Berechnung bei gleichzeitig guter Rechengeschwindigkeit. Hier empfiehlt sich folgende Einstellung:

• Anfänglicher Substep: 100.
  Das bedeutet: wir beginnen mit 1/100 der Last
• Min Substep: 10.
  Das bedeutet: es werden mindestens 10 Lastschritte gewählt
• Max Substep: 1000.

Das bedeutet: es werden maximal 1000 Lastschritte gewählt.

Ansys Workbench passt jetzt abhängig von der Komplexität der Berechnung die Lastschritte automatisch an.

4.4 Netzfeinheit und Elemente

Für die Güte der Berechnungsergebnisse ist die Netzfeinheit und die Elementwahl entscheidend. In unserem Artikel zur Auswahl der richtigen Elemente für eine FEM haben wir gezeigt, dass Tetraederelemente mit Seitenmittenknoten eine gute Wahl sind.

Der zweite Artikel zur richtigen Netzfeinheit für FEM Berechnungen zeigt, dass Bauteile mit mindestens 5 Elementen über dem Viertelkreis vernetzt werden sollten.

4.5 Randbedingungen

Der Haken wurde mit einer Hakenlast von 40 kN belastet. Die Kraft wurde als Bolzenlast aufgebracht und der Haken in der Öse über eine zylindrische Lagerung festgehalten. Aus Symmetriegründen wurde nur eine Hälfte des Hakens simuliert und die Schnittstelle durch eine Reibungsfreie Lagerung abgebildet. Alle Randbedingungen sind in folgender Abbildung zu sehen.

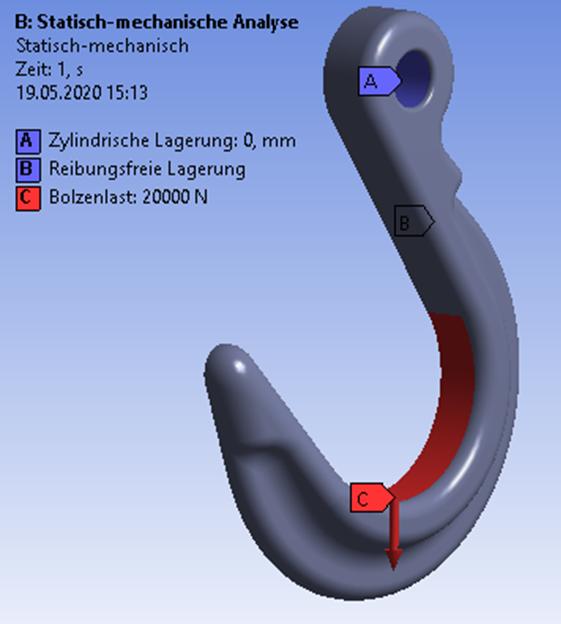
Randbedingungen zur Simulation des Kranhakens

4.6 Berechnung

Damit sind alle Eingaben gemacht und wir starten die Analyse durch F5 oder den Button Lösung.

5 Berechnung der plastischen Formzahl mit FEM

Eine detaillierte Beschreibung der plastischen Stützzahl n_pl nach der FKM Richtlinie finden Sie in unserm Artikel zur Neuber-Regel und der plastischen Stützzahl. Kurz zusammengefasst besteht die plastische Stützzahl aus zwei Teilen, von denen das kleiner maßgeblich ist:

n_pl = MIN([E · ε_ert  / R_e]^1/2; K_p).

1. Dem Dehnungskriterium und
2. Der Traglast, welche durch die plastische Formzahl K_p beschrieben wird.

Das Dehnungskriterium sichert gegen die vom Material ertragbare Dehnung (ε_ert) ab. Dieses Kriterium lässt sich sehr gut analytisch berechnen.

Die Traglast sichert gegen eine Plastifizierung des Nettoquerschnitts ab und wird durch die plastische Formzahl K_p beschrieben. Die plastische Formzahl lässt sich analytisch nur für sehr einfache Geometrien berechnen. Deshalb wird dafür die FEM benötigt.

Vor allem für gekerbte Bauteile aus duktilen Werkstoffen mit niedriger Festigkeit ist oftmals die Traglast das begrenzende Kriterium, weshalb sich hier eine genaue Berechnung mit FEM lohnen kann.

Die plastische Formzahl ist definiert als das Verhältnis aus der Last bei welcher der Querschnitt vollplastisch ist (vollplastische Traglast L_{vollplastisch}) zur elastischen Grenzlast L_elastisch:

K_p = L_{vollplastisch} / L_elastisch.

L_elastisch ist die Last, bei der an der höchst beanspruchten Stelle gerade die Streckgrenze Erreicht wird. L_{vollplastisch} ist die Last, bei der der gesamte Querschnitt plastisch verformt ist.

5.1  Ermittlung der vollplastischen Traglast L_{vollplastisch}

Für unseren Kranhaken sieht das FEM Ergebnis der plastischen Berechnung wie folgt aus.

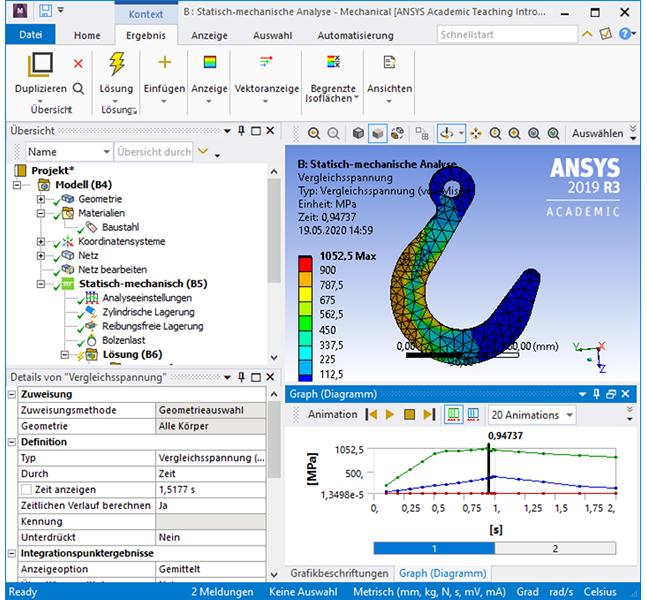
Ergebnisse der vollplastischen FEM zur Ermittlung der plastischen Traglast

In obiger Abbildung ist das Ergebnis der Berechnung zu erkennen. Dargestellt ist das Ergebnis im Lastschritt 0,94737. Das bedeutet, dass diesem Lastschritt die Last von

F_0,94737 = 0,94737 * Maximallast = 0,94737 * 40 kN = 38 kN zugeordnet ist.

Die Farbskala wurde so eingestellt, dass die Ockerfarbenen Bereiche etwa im Bereich der Streckgrenze von 900 MPa liegen. In diesem Lastschritt ist jetzt quasi der gesamte Querschnitt plastisch verformt, da die Spannungen alle im Bereich der Streckgrenze liegen.

Damit ist die Kraft von F_0,94737 die vollplastische Traglast

L_{vollplastisch} = F_0,94737 = 38 kN.

Eine etwas andere Darstellung kann ebenfalls zum Ziel führen. Hier tragen wir uns die Ergebnisse aller Lastschritte im Excel als Diagramm auf. Und zwar indem wir die Kraft über der Gesamtverformung auftragen:

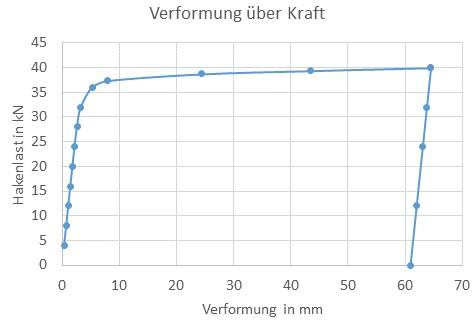
Ergebnis der FEM: Kraft über Verformung

Wir erkennen in dem Diagramm bis etwa 32…37 kN einen linearen Zusammenhang zwischen Kraft und Gesamtverformung. Für Kräfte größer 37 kN nimmt die Verformung überproportional zu. Der Haken verformt sich plastisch.

Dieser Übergang vom linearen in den nichtlinearen Bereich ist durch die vollplastische Traglast L_{vollplastisch} gekennzeichnet. In dieser Abbildung bei

L_{vollplastisch} = 32 kN.

5.2 Ermittlung der elastischen Grenzlast L_elastisch

Zur Ermittlung der elastischen Grenzlast sucht man sich einen beliebigen Lastschritt im elastischen Bereich aus (z. B. den ersten Lastschritt 0,1). Für diesen Lastschritt wird die Spannung abgelesen und dann mittels Dreisatzes auf die elastische Grenzlast umgerechnet.

Folgende Abbildung zeigt die Ergebnisse für den Lastschritt 0,1.

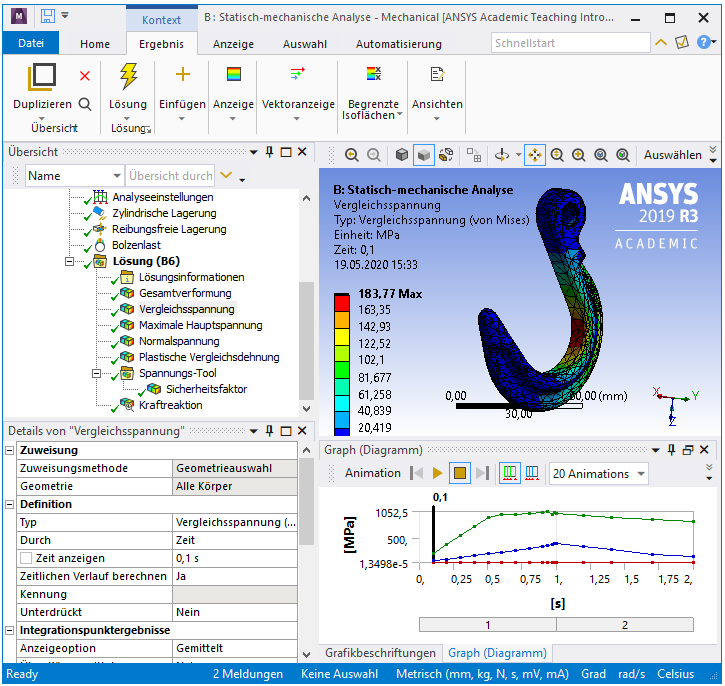
Ergebnisse der FEM Berechnung zur Ermittlung der elastischen Grenzlast

Bei dem Lastschritt 0,1 ergibt sich eine Vergleichsspannung von σ_0,1 = 183 MPa. Diesem Lastschritt ist die Kraft

F_0,1 = 0,1 * Maximallast = 0,1 * 40 kN = 4 kN

zugeordnet. Wenn die Spannung die Streckgrenze von R_e = 900 MPa erreicht, ist genau die elastische Grenzlast erreicht. Da es sich hier um eine lineare FEM handelt, können die Ergebnisse mit dem Dreisatz umgerechnet werden:

F_0,1 / σ_0,1 = L_elastisch / R_e

umformen liefert:

L_elastisch / R_e = F_0,1 / σ_0,1

L_elastisch = F_0,1 / σ_0,1 * R_e = 4 kN /183 MPa * 900 MPa = 19 kN.

Damit ist die elastische Grenzlast bei 19 kN.

5.3  Berechnung der plastische Formzahl K_p

Nach obiger Gleichung ist die plastische Formzahl das Verhältnis aus

K_p = L_{vollplastisch} / L_elastisch = 32 kN / 19 kN = 1,68.

Dies bedeutet, dass 64% höhere Lasten zugelassen werden können, als nach konventioneller Annahme!

Würde die plastische Formzahl nach der FKM Richtlinie abgeschätzt werden, würde man mit K_p = 1,5 rechnen müssen.

Wir sehen: der Aufwand einer elastische plastischen FEM wird mit einer etwas höheren plastischen Formzahl belohnt. Die Belohnung fällt umso größer aus, je

• duktiler der Werkstoff
• geringer die Streckgrenze und
• schärfer gekerbt das Bauteil ist.

Unser Kranhaken weist ja kaum eine Kerbe auf, daher der geringe Unterschied zwischen den beiden plastischen Formzahlen.

6 Auf den Punkt