Die Neuber-Regel. Oder: warum plastische Verformungen gut sind und wie Sie Bauteile mit der plastischen Stützzahl höher auslasten
Oftmals können statisch belastete Bauteile noch höher ausgelastet werden. Wenn Sie diese Festigkeitsreserven heben wollen, dann lohnt es sich die plastische Formzahl (z. B. analog der FKM-Richtlinie) genauer zu berechnen. Erfahren Sie hier, was dies ist, wie dieser mit der Neuber-Regel zusammenhängt und wie Sie diese berechnen können.
In diesem Artikel lernen Sie,
- was die Neuber-Regel ist, und wie Sie diese anwenden können und wie diese hergeleitet wird,
- wie Sie plastische Dehnungen auch ohne eine aufwändige plastische FEM Berechnungen ermitteln können,
- Festigkeitsreserven zu heben, indem Sie die plastische Stützzahl npl und die vollplastische Formzahl Kp berechnen,
- worauf Sie bei der Berechnung der plastischen Formzahl Kp mit FEM achten müssen
- wie groß die Potenziale sind.
Inhalt
1 Grundlagen
Insbesondere bei gekerbten Bauteilen treten die maximalen Spannungen oftmals stark konzentriert in den Kerben auf. Überschreiten die Kerbspannungen die Streckgrenze, plastifiziert der Werkstoff lokal eng begrenzt. Mit einer globalen Verformung oder dem Versagen des Bauteiles ist deswegen nicht zu rechnen. Siehe folgende Abbildung.
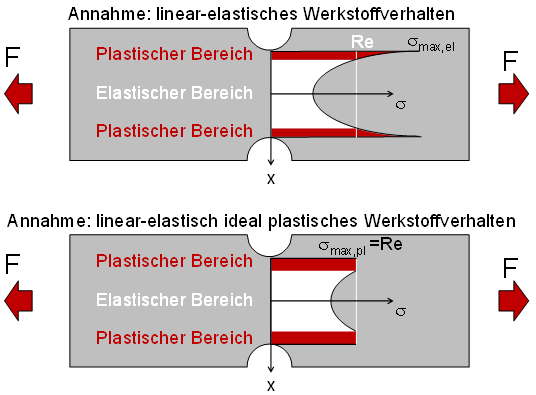
Erklärung der Spannungsumlagerung auf Grund von plastischen Verformungen
Es werden die hoch beanspruchten (plastisch verformten) Bereiche des Bauteils durch die noch elastisch beanspruchten Bereiche gestützt. Für den Festigkeitsnachweis können deshalb für die höchst beanspruchte Stelle plastische Dehnungen zugelassen werden. Man spricht deshalb auch von einer Stützwirkung.
Die folgende Abbildung zeigt eine FEM Berechnung unter Annahme von linearelastisch-idealplastischem Werkstoffverhalten. Die Skala der FEM Berechnung ist so eingestellt, dass allen Spannungen ab der Streckgrenze die rote Farbe zugewiesen wird. Im linken Teil der Abbildung ist der Verlauf der Last (Kraft F) über der Verformung dargestellt.
Bei der Last Lelastisch wird an der höchst beanspruchten Stelle gerade die Streckgrenze erreicht. Der größte Teil des Querschnitts sieht nur elastische Verformungen. Wird die Last weiter gesteigert (F > Lelastisch) erfahren immer größere Bereiche eine plastische Verformung. Bei Erreichen der Kraft F = Lvollplastisch erfährt der gesamte Querschnitt eine plastische Verformung.
Im Kraft-Verschiebungsdiagramm (linkes Bild von unterer Abbildung) sieht man, dass das globale Bauteilverhalten bis zur Kraft Lvollplastisch noch linear ist. Erst für Kräfte oberhalb von Lvollplastisch verformt sich das Bauteil global plastisch. Diese Last wird als Traglast bezeichnet.
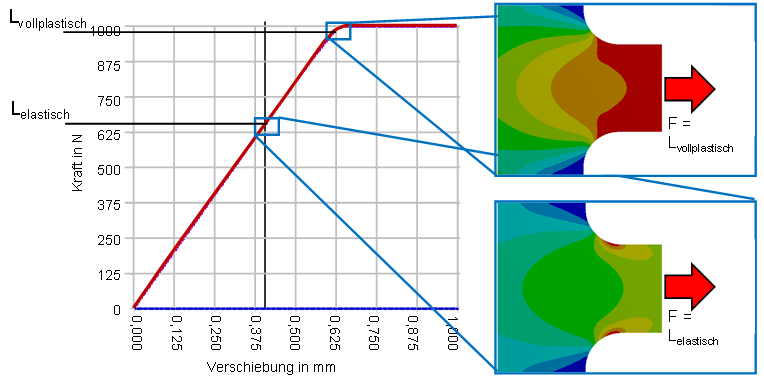
Die Ermittlung der vollplastische Formzahl Kp mit FEM
Bauteile bei denen plastische Dehnungen zugelassen werden, müssen deshalb gegen zwei Versagensmechanismen abgesichert werden:
- gegen zu große plastische Dehnungen (das Dehnungskriterium) und
- gegen große Verformungen (die Traglast).
Mathematisch wird der Einfluss der plastischen Dehnung durch die plastische Stützzahl npl beschrieben. Die Berechnung der plastischen Dehnungen und damit der plastischen Stützzahl fußt auf der Neuber-Regel.
2 Eine Analogie aus dem Alltag
Will man ein Loch in ein Metallblech bohren, wird üblicherweise vorgekörnt. Dies verhindert das weglaufen des Bohrers. D. h. man treibt die Spitze eines Körners durch einen Hammerschlag an der zu bohrenden Stelle in das Material. Dadurch wird eine kleine Mulde im Werkstoff erzeugt, in welche die Bohrerspitze eingesetzt werden kann und dann nicht mehr wegläuft.

Körner zum Anbringen einer Körnung im Metall
Will man ein Loch in ein Glas bohren, wird dagegen nicht vorgekörnt. Denn dies würde sofort zum Bruch der Glasscheibe führen.
Was kann man daraus schließen?
In beiden Fällen führt der Hammerschlag auf den Körner zu sehr hohen Spannungen an der Körnerspitze. Denn die Hammerspitze ist sehr klein, und dadurch entstehen selbst bei kleinen Kräften sehr hohe Spannungen. Diese liegen deutlich über der Streckgrenze und z. T. über der Zugfestigkeit des Bauteils.
Nach der klassischen Festigkeitslehre müssten beide Werkstoffe also brechen. Die Praxis gibt ein anderes Bild. Ursächlich dafür ist, dass es sich bei dem Metallblech um ein duktiles (weiches, verformungsfreudiges) und bei dem Glas um ein sprödes Material handelt. Im ersten Fall wird der Werkstoff plastifizieren. Es werden die hohen Spannungen also durch plastische Verformungen umgelagert. Dagegen hat das Spröde Glas diese Möglichkeiten nicht.
D. h. duktile Werkstoffe haben das Potenzial plastische Verformungen problemlos bis zu einer gewissen Grenze zu ertragen. Diese Potenziale werden durch die plastische Stützzahl npl im Maschinenbau berücksichtigt und auf Basis der Neuber-Regel berechnet.
Es muss jedoch sichergestellt werden, dass sich das Bauteil nicht global so stark plastisch verformt, dass dessen Funktion nicht mehr gewährleistet werden kann. Diesen Nachweis führt man über die vollplastische Formzahl Kp.
Für den Festigkeitsnachweis müssen immer beide Faktoren (die plastische Stützzahl npl → das Verformungskriterium und die vollplastische Formzahl Kp → die Traglast) berücksichtigt werden.
2 Die Neuber-Regel
Um plastische Dehnungen in der Bauteilauslegung zulassen zu können, müssen diese berechnet werden. Dafür wird gerne die FEM genutzt und das reale Spannungs-Dehnungsdiagramm als Werkstoffgesetz genutzt.
Mit Hilfe der Neuber-Regel können linearelastische Spannungen in elastisch-plastischen Spannungen analytisch, also ohne FEM umgerechnet werden. Dies gibt einem einen großen Vorteil bezüglich der Rechenzeit.
Begrenzt ist die folgende Form der Neuber-Regel auf Bauteile, bei denen der Nettoquerschnitt nicht plastifiziert. Es dürfen also nur die Kerbspannungsanteile plastifizieren.
Möchte man auch Bauteile berechnen, bei denen der Nettoquerschnitt plastifiziert, dann muss mit der erweiterten Neuber-Regel gearbeitet werden.
3.1 Definition der Neuber-Regel
Die Neuber-Regel ist dadurch definiert, dass das Produkt aus Spannung und Dehnung immer konstant ist:
Spannung · Dehnung = konstant.
Alle Punkte die dieser Funktion genügen liegen auf einer Hyperbel, wie die Umformung obiger Gleichung nach der Spannung zeigt:
Spannung = Konstante/Dehnung.
Deshalb wird diese Funktion auch als Neuber-Hyperbel bezeichnet. Grafisch bedeutet die Neuber-Regel, dass die Fläche unterhalb der Hyperbel für jeden Punkt gleich ist. Siehe dazu auch die folgende Abbildung.
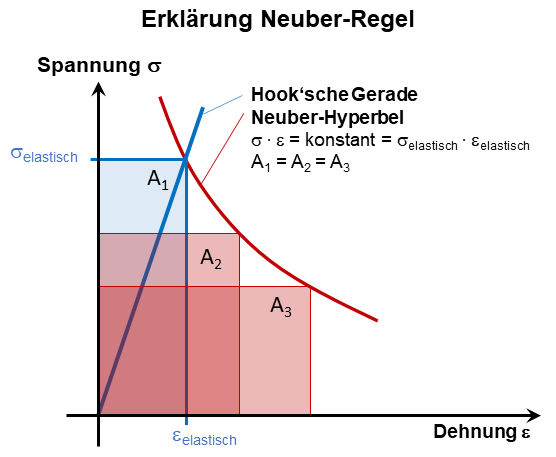
Erklärung der Neuber-Regel und der Neuber-Hyperbel
Das bedeutet, dass das Produkt aus Spannung und Dehnung bei rein linearelastischem Werkstoffverhalten gleich dem Produkt aus Spannung und Dehnung bei Verwendung des elastisch-plastischen Werkstoffverhaltens ist:
Linearelastische Spannung · linearelastische Dehnung = elastisch-plastische Spannung · elastisch-plastische Dehnung
3.2 Anwendung der Neuber-Regel
Was bringt jetzt die Neuber-Regel, wie kann diese im Alltag genutzt werden? Denn obige Gleichung
Linearelastische Spannung · linearelastische Dehnung = elastisch-plastische Spannung · elastisch-plastische Dehnung
alleine hat noch keine direkte Anwendung, da sie zwei Unbekannte enthält, die gesucht sind. Das sind die elastisch-plastische Spannung und die elastisch-plastische Dehnung. Erst wenn man eine (beliebige) reale Spannungs-Dehnungskurve vorgibt, lässt sich das Problem lösen.
Im Falle von statischen Berechnungen wird oftmals linearelastisch-idealplastisches Werkstoffverhalten angenommen. Zeichnet man dieses Werkstoffgesetz zu der Hook’schen Gerade und der Neuberhyperbel ein, ergibt sich folgendes Bild.
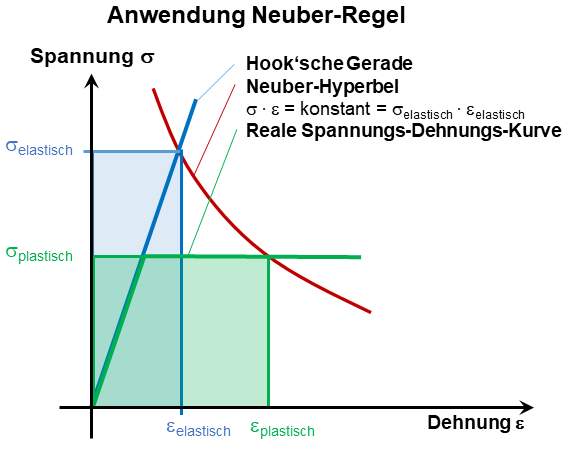
Anwendung der Neuber-Regel
Bei der grafischen Lösung der Neuber-Regel liefert der Schnittpunkt der Neuber-Hyperbel mit der Spannungs-Dehnungs-Kurve die elastisch-plastische Spannung σplastisch und die elastisch-plastische Dehnung εplastisch.
Rechnerisch wird wie folgt vorgegangen:
Linearelastische Spannung · linearelastische Dehnung = elastisch-plastische Spannung · elastisch-plastische Dehnung
σelastisch · εelastisch = σplastisch · εplastisch
Im Falle des linearelastisch-idealplastischen Werstoffgesetzes gilt für die Spannung
σplastisch = Re
außerdem hängen σelastisch und εelastisch über das Hook’sche Gesetz voneinander ab, so dass gilt:
εelastisch = σelastisch / E
Damit gilt für obige Gleichung:
σelastisch · εelastisch = σplastisch · εplastisch
σelastisch · σelastisch / E = Re · εplastisch
(σelastisch)2 / E = Re · εplastisch
Durch Umformen dieser Gleichung nach εplastisch bzw. σelastisch Jetzt können zwei Dinge berechnet werden.
- es kann bei einer gegebenen Spannung aus einer linearelastischen FEM Berechnung σelastisch auf die elastisch-plastische Dehnung εplastisch geschlossen werden:
εplastisch = (σelastisch)2 / (E · Re) oder - es kann bei einer gegebenen elastisch-plastischen Dehnung auf die zugehörige Spannung aus einer linearelastischen FEM Berechnung σelastisch und damit auf die zu Grunde liegende Belastung geschlossen werden:
σelastisch = (Re · εplastisch · E)1/2
Besonders spannend ist Gleichung 2. Denn was bedeutet diese Gleichung?
Gibt man jetzt als plastische Dehnung eine vom Werkstoff ertragbare Dehnung vor (εplastisch = εert), dann erhält man die zugehörige ertragbare Spannung bei linearelastischer Berechnung.
3.3 Herleitung der Neuber-Regel
Was steckt hinter dem Grundgedanken der Neuber-Regel? Um dies zu verstehen, können wir die Neuber- Regel auch etwas anders schreiben:
Spannung · Dehnung = konstant.
σelastisch · εelastisch = konstant
Ersetzt man jetzt die elastische Dehnung durch
εelastisch = ΔL/L0
und die elastische Spannung durch
σelastisch = F/A
so erhält man
σelastisch · εelastisch = konstant
F/A · ΔL/L0 = konstant
(F · ΔL) / (A · L0) = konstant
Wobei
A · L0 = Fläche · Länge = Volumen und
F · ΔL = Kraft · Längenänderung = Arbeit ist.
Arbeit / Volumen = konstant.
Das bedeutet, egal ob linear-elastisches oder elastisch-plastisches Materialverhalten angenommen wird, es ist in beiden Fällen dieselbe Arbeit (Energie) pro Volumen nötig, um das Bauteil bei der angenommenen Last zu verformen.
4 Die plastischen Stützzahl (Dehnungskriterium)
4.1 Definition der plastischen Stützzahl
Die plastische Stützzahl npl beschreibt die Fähigkeit eines Bauteils, Tragreserven durch bewusstes zulassen plastischer Dehnungen auszuschöpfen. Dies führt dazu, dass Lasten zugelassen werden, welche im Bauteil zu Spannungen über der Streckgrenze führen! Möglich ist dies durch die Umlagerung von Spannungen in die weniger hoch beanspruchten Bereiche.
Genutzt wird die Stützzahl in vielen modernen Regelwerken, wie etwa der FKM-Richtlinie.
4.2 Berechnung der plastischen Stützzahl
In modernen Festigkeitsnachweisen wie der FKM-Richtlinie sind (wie oben beschrieben) zwei Kriterien zur Berechnung der plastischen Stützzahl notwendig:
- Das Dehnungskriterium: Es muss gegen eine vom Bauteil ertragbare Gesamtdehnung εert abgesichert werden
([E · εert / Re]1/2, mit dem E-Modul E und der Streckgrenze Re) und - Die Traglast: Zum anderen muss durch die plastische Formzahl Kp sichergestellt werden, dass nicht der gesamte Bauteilquerschnitt plastisch verformt ist
(Kp = vollplastische Traglast (LVollplastisch) / elastische Grenzlast (Lelastisch)).
Ausgelegt wird dann gegen den kleineren der beiden Faktoren. Das Vorgehen zeigt folgende Abbildung schematisch. Berechnet wird die plastische Stützzahl nach
npl = MIN([E · εert / Re]1/2; Kp).

Visualisierung der Berechnung der plastischen Stützzahl
Zur Berechnung des Dehnungskriteriums wird neben dem E-Modul und der Streckgrenze noch die ertragbare Dehnung eert benötigt. Typische Werte für die ertragbare Dehnung eert liefert die FKM Richtlinie:
| Stahl | GJS | GJM | Alu Knetlegierung | Alu Guss | |
| εert in % | 5 | 4 | 2 | 5 | 2 |
Zur Berechnung der Traglast kann die FEM bemüht werden. Alternativ gibt einem die FKM-Richtlinie konservative Werte für die plastische Formzahl Kp an die Hand.
| Querschnitt | Biegung Kp,b | Torsion Kp,t |
| Kreis | 1,7 | 1,33 |
| Kreisring (dünnwandig) | 1,27 | 1 |
| Rechteck | 1,5 | Nur mit FEM berechenbar! |
In einem folgenden Artikel werden wir uns mit der Berechnung der plastischen Formzahl Kp befassen.
4.3 Herleitung der plastischen Stützzahl
Ziel ist es immer, die Spannungen im Bauteil linearelastisch zu berechnen. Das hat die Vorteile, dass die Berechnung sehr einfach, schnell und mit FEM oder auch analytisch möglich ist. Gleichzeitig lassen sich dadurch auch elastisch-plastische FEM-Berechnungen einfach validieren.
Weiter oben haben wir die Neuber-Regel durch umformen auf folgende Gleichung gebracht:
σelastisch = (Re · εplastisch · E)1/2 = Re · (εplastisch · E / Re)1/2
Werden jetzt Dehnungen zugelassen (εert), die auch plastische Dehnungsanteile enthalten, dann sind die Spannungen größer als die Streckgrenze. Deshalb werden natürlich die linearelastisch berechneten Spannungen selastisch von den realen (elastisch-plastischen) Spannungen abweichen. Mit obiger Gleichung können diese berechnet werden. Setzt man εplastisch = εert erhält man:
σelastisch =Re · (εert · E / Re)1/2
Nach dieser Gleichung führen linearelastische Spannungen σelastisch, die um den Faktor (εert · E / Re)1/2 oberhalb der Streckgrenze liegen genau zu der ertragbaren Dehnung εert. Diese Gleichung zeigt also deutlich, dass bei Zulassen von plastischen Dehnungen die Spannungen bei linearelastischer Berechnung deutlich oberhalb der Streckgrenze liegen können. Und zwar genau um den Betrag des Dehnungskriteriums aus obigem Abschnitt. Link einfügen!!!xxx
Fazit:
Das Dehnungskriterium ist genau aus der Neuber-Regel unter der Annahme von linearelastisch-idealplastischem Werkstoffverhalten abgeleitet.
5 Fazit
Das Dehnungskriterium ([E · εert / Re]1/2) erhöht also die Streckgrenze, so dass sich bei linearelastischer Berechnung der Spannungen im Bauteil genau die ertragbare Dehnung εert einstellt, wenn linearelastisch-idealplastisches Werkstoffverhalten angenommen wird.
Die Potenziale, die sich dadurch erschließen sind enorm, wenn ein Bauteil ausreichend duktil ist und sich eine ungleiche Spannungsverteilung im Bauteil einstellt! Denn dann sind die Möglichkeiten zur Spannungsumlagerung ideal. ABER: gleichzeitig bedeutet eine ungleiche Spannungsverteilung z. B. wegen Kerben auch, dass das Bauteil nicht hoch genug ausgelastet ist. Besser ist immer die Kerbwirkung zu reduzieren!
6 Potenziale
Nachfolgend drei Beispiele für die Potenziale die sich durch Ausnutzen der plastischen Stützzahl ergeben. Bei allen drei Beispielen zeigt sich, dass durch das Zulassen von plastischen Dehnungen deutlich höhere Lasten zugelassen werden können. In diesen Beispielen um bis zu 70%!
- Ein Vergütungsstahl C60
Re = 370 MPa
E = 210 000 MPa
A = 10 %
Kp = 1,7 (Annahme: Kreisquerschnitt unter Biegung, siehe obige Tabelle)
εert = 5 % (siehe obige Tabelle)
[E · εert / Re]1/2 = [210 000 · 0,05 / 370]1/2 = 5,3
npl = MIN([E · εert / Re]1/2; KP) = MIN(5,3; 1,7) = 1,7Fazit 1: Nach dem Dehnungskriterium können 5,3 mal höhere Lasten zugelassen werden.
Fazit 2: Maßgeblich ist allerdings die Traglast, nicht das Dehnungskriterium!
Fazit 3: Deshalb können in Summe „nur“ 1,7 mal höhere Lasten zugelassen werden!
Fazit 4: Um noch höhere Lasten zulassen zu können, müsste die plastische Formzahl Kp mit FEM genauer berechnet werden. - Eine Aluminiumlegierung AlMgSi T6
Re = 160 MPa
E = 70 000 MPa
A = 12%
Kp = 1,0 (Annahme: Kreisquerschnitt unter Zug, siehe obige Tabelle)
εert = 5 % (siehe obige Tabelle)
[E · εert / Re]1/2 = [70 000 · 0,05 / 160]1/2 = 4,7
npl = MIN([E · εert / Re]1/2; KP) = MIN(4,7; 1,0) = 1,0Fazit 1: Nach dem Dehnungskriterium können 4,7 mal höhere Lasten zugelassen werden.
Fazit 2: Maßgeblich ist allerdings die Traglast, nicht das Dehnungskriterium!
Fazit 3: Deshalb können keine höhere Lasten zugelassen werden!
Fazit 4: Um noch höhere Lasten zulassen zu können, müsste die plastische Formzahl Kp mit FEM genauer berechnet werden. - Ein Gusseisenwerkstoff EN-JM 1170
Re = 390 MPa
E = 180 000 MPa
A = 3 %
Kp = 1,7 (Annahme: Kreisquerschnitt unter Biegung, siehe obige Tabelle)
εert = 2 % (siehe obige Tabelle)
[E · εert / Re]1/2 = [180 000 · 0,02 / 390]1/2 = 3,0
npl = MIN([E · εert / Re]1/2; Kp) = MIN(3,0; 1,7) = 1,7Fazit 1: Nach dem Dehnungskriterium können 4,7 mal höhere Lasten zugelassen werden.
Fazit 2: Maßgeblich ist allerdings die Traglast, nicht das Dehnungskriterium!
Fazit 3: Deshalb können in Summe „nur“ 1,7 mal höhere Lasten zugelassen werden!
Fazit 4: Um noch höhere Lasten zulassen zu können, müsste die plastische Formzahl Kp mit FEM genauer berechnet werden.
7 Auf den Punkt
- Die plastische Stützzahl npl beschreibt die Fähigkeit eines Bauteils, Tragreserven durch bewusstes zulassen plastischer Dehnungen auszuschöpfen. Dies führt dazu, dass Lasten zugelassen werden, die im Bauteil zu Spannungen führen, die über der Streckgrenze liegen.
- Durch das zulassen plastischer Dehnungen im Bauteil können Festigkeitsreserven gehoben werden.
- Dies gilt insbesondere bei duktilen Werkstoffen und bei Bauteilen die eine ungleichförmige Spannungsverteilung über den Querschnitt aufweisen.
- Bei modernen Regelwerken sind zwei Kriterien zu berücksichtigen,
- das Dehnungskriterium
- die Traglast
- Erfahrungsgemäß ist vor allem bei duktilen und niedrigfesten Bauteilen die Traglast das begrenzende Kriterium und nicht das Dehnungskriterium
- In einem der folgenden Artikel wird deshalb die Berechnung der Traglast mit der FEM besprochen und aufgezeigt, wie die plastische Formzahl Kp ermittelt werden kann.
- Wenn Sie an der Berechnung der Neuber-Regel mit Excel interessiert sind: wir haben ein schönes Excel-Tool zur Visualisierung der Neuber-Regel.
Die Berechnung der plastischen Formzahl wurde in diesem Artikel nicht behandelt. Dieser Artikel zeigt Ihnen schritt für Schritt, wie Sie die plastische Formzahl in FEM berechnen.
Weiterführende Informationen zur FKM Richtlinie und Wöhlerkurven
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Betriebsfestigkeit mit FEM
Das Seminar zur Betriebsfestigkeit gibt Ihnen einen guten Überblick über die Methoden der Betriebsfestigkeit und der FEM. Hier lernen Sie
✓ alle wichtigen Methoden kennen, um Ihre Bauteile robust auf die Betriebsfestigkeit auszulegen.
✓ Schweißverbindungen auszulegen.
✓ verstehen, welche Faktoren die Lebensdauer Ihrer Bauteile besonders stark beeinflussen.
✓ Grundlagen der Finite-Elemente-Ergebnisse (FEM) kennen, anzuwenden und zu interpretieren.
✓ Lastkollektive mit Hilfe der Rainflowzählung zu ermitteln.
✓ eine Wöhlerlinie für Ihre Bauteile rechnerisch abzuschätzen.
✓ Bauteillebensdauern mittels Schadensakkumulation zu berechnen.
✓ Dauerschwingfestigkeitsnachweise zu führen.
✓ die modernen Regelwerke wie die FKM Richtlinie zur Betriebsfestigkeitsbewertung kennen.
Seminare zur FKM Richtlinie:
Haben Sie Interesse an einer schnellen Anwendung und einem einfachen Einstieg in die komplexe FKM Richtlinie? Dann ist unsere Schulung zur FKM Richtlinie für Sie richtig.
Diese ist genau richtig für Sie, wenn Sie
✓ die FKM Richtlinie schnell anwenden möchten.
✓ Ihre FEM Ergebnisse bewerten wollen.
✓ die Hintergründe der FKM Richtlinie verstehen und üben wollen.
Weiterführende Literatur
 Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses führt Sie schnell und verständlich in die Versuche und die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auslegung Ihrer Bauteile auf die Dauerfestigketi oder Betriebsfestigkeit. Sie können dann einfach Wöhlerlinien für Ihre Bauteile berechnen.
Hilfreiche Software:

Wir haben basierend auf unserer jahrelangen Erfahrung, der Mitarbeit in den Forschungsgremien zur FKM Richtlinie und dem praktischen Arbeiten mit der Richtlinie FKMmadeEASY- die Excel-Software zur FKM Richtlinie entwickelt. Wir haben dabei speziell darauf geachtet, dass diese Software
✓ einfachst möglich bedienbar
✓ gut dokumentiert und nachvollziehbar sowie
✓ optisch ansprechend ist (es soll ja auch Spaß machen).
Überzeugen Sie sich selbst davon anhand der Testversion von FKMmadeEASY - die Excel-Software zur FKM Richtlinie
Der Autor:
Bildernachweis
Bild Körner
Bild von Bernhard Stärck auf Pixabay

Like!! I blog quite often and I genuinely thank you for your information. The article has truly peaked my interest.
Thanks for your kind Feedback!
regards
Stefan
Guten Tag,
meine Frage ist bezogen auf die ertragbare Dehnung vom Stahl.
Im elastichen Bereich liegt diese bei 5% (elastische Dehnung) und im plastischen Bereich bei 15% (plastiche Dehnung) nach DNV-Richtlinie.
Gerne möchte ich bitte fragen, warum bei der Neuber-Formel die elastische Dehnung von 5% und nicht die plastische Dehnung von 15 % für Stahl zum Beipiel genommen wird?
Vielen Dank
Youssef
Hallo Youssef,
Die Angaben in dem Artikel beziehen sich auf die Verwendung von Nennspannungen.
Bei den 5% handelt es sich um die zulässige Gesamt-Dehnung (also elastische plus plastische Dehnung). Ich habe diese Dehnung gewählt, da es die konservative Annahme ist.
In der FKM Richtline Rechnerischer Festigkeitsnachweis von 2012 wird bei der Berechnung auf Basis von FEM Spannungen eine ertragabare Dehnung angegeben, die in der Größenordnung der Bruchdehnung A liegt.
Leider kenne ich die DNV Richtlinie nicht. Welche meinen Sie denn? Hier gibt es ja sehr viele? Können sie mir diese senden?
Beantwortet dies deine Frage?
Schöne Grüße und bleiben Sie gesund
Stefan
Merely needed to mention I’m just glad I stumbled upon your web site.
Thanks for your response!
Hallo und Danke für den schönen Artikel,
Wie ist die Grundlegende Gleichung auf der die Neuber-Regel basiert motiviert:
Spannung · Dehnung = konstant
Aus dem allgemeinen Arbeitssatz kommt diese Gleichung ja nicht oder? Soweit ich die Annahme verstehe bedeutet sie.
Formänderungsenergiedichte + komplementäre Formänderungsenergiedichte = konstant
Aber wie wird das begründet?
Liebe Grüße,
Andreas
Hallo Andreas,
Neuber beschreibt das Verhalten der Schubspannungen und Schubverformungen im Kerbbereich gekerbter Körper.
Dabei hat er festgestellt, dass bei Annahme von linearelastischem und elastisch plastischem Werkstoffverhalten geschlossene Lösungen möglich sind.
Bei der Neuber-Regel fokussiert sich Hr. Neuber nur auf die maximale Spannung im Kerbgrund.
Er beschreibt außerdem, dass
beschrieben werden und alle drei über diese Gleichung zusammenhängen:
(ασ * αε)0,5 = αH
Um die Ergebnisse von den Schubspannungen auf die Normalspannungen zu übertragen, verwendet Neuber dann die Vergleichsspannung nach der der Gestaltänderungs-Energie-Dichte Hypothese (GEH).
Die Quelle ist:
Neuber, H.; Theory of Stress Concentration for Shear-Strained Prismatical Bodies With Arbitrary Nonlinear Stress-Strain Law; 1961, S. 544-550, Journal of Applied Mechanics.
Schöne Grüße und viel Spass beim Arbeiten mit der Neuber-Regel
Stefan