Den Spannungsgradienten aus der FEM Simulation richtig auswerten
Berechnen Sie Ihre Bauteile auch mit der FEM und führen Sie einen Betriebsfestigkeitsnacheis? Dann kennen Sie sicherlich die Unsicherheit, worauf genau es bei der Auswertung des Spannungsgradienten ankommt. In diesem Artikel erfahren Sie, wie Sie den Spannungsgradienten aus Ihren FEM Ergebnissen auswerten.
Wenn Sie einen Nachweis der Betriebsfestigkeit führen (z.B. nach der FKM-Richtlinie) spielt die Stützwirkung eine wichtige Rolle. Die Stützwirkung beschreibt dabei das Phänomen, dass bei gekerbten Bauteilen die schwingend belastet werden die Kerben nicht so kritisch auswirken, wie dies bei statischer Belastung der Fall wäre. Nach Stieler, bzw. Siebel hängt die Stützwirkung vom Spannungsgradienten und der Werkstofffestigkeit ab.
In diesem Artikel lernen Sie,
- die Definition des Spannungsgradienten kennen
- wie Sie den Spannungsgradienten berechnen, z.B. für die FKM Richtlinie
- worauf es bei der Modellierung in der FEM ankommt, um den Spannungsgradienten aus der FEM auszuwerten
- wertvolle Tipps für eine effiziente Auswertung kennen.
Inhalt
Grundlagen
Je schwächer die Kerbe ist,
- umso flacher ist auch der Spannungsabfall ins Bauteilinnere und
- umso größer sind die hochbeanspruchten Bereiche.
Die Stützwirkung und damit die Stützziffer nχ sinken. Die Stützwirkung nimmt also mit sinkender Kerbschärfe bzw. mit einem flacheren Spannungsabfall ab. Der Spannungsabfall wird durch den bezogenen Spannungsgradienten χ* beschrieben. Je genauer die Stützwirkung bekannt ist, umso höhere Lasten können zugelassen werden. Die Bauteile können also besser ausgelastet werden. Deshalb ist es wichtig den Spannungsgradienten möglichst genau zu berechnen. Neben analytischen Näherungslösungen wird der Spannungsgradient oft aus FEM Ergebnissen berechnet.
Die Definition des Spannungsgradienten
Der Spannungsgradient
ist dabei der Spannungsabfall im Kerbbereich oder die Steigung des Spannungsabfalles. Dieser ist von der Beanspruchungshöhe (der Maximalspannung σmax) abhängig. Zur Vermeidung dieses Einflusses wird der bezogene Spannungsgradient χ* berechnet. Den bezogenen Spannungsgradient erhält man, wenn der Spannungsgradient auf die Maximalspannung normiert wird, siehe folgende Abbildung/Gleichung:
Dabei ist Δσ der Spannungsabfall über dem Bereich Δx. Der bezogene Spannungsgradient χ* kann entweder aus Simulationsergebnissen, durch Messungen oder aus Tabellen ermittelt werden.
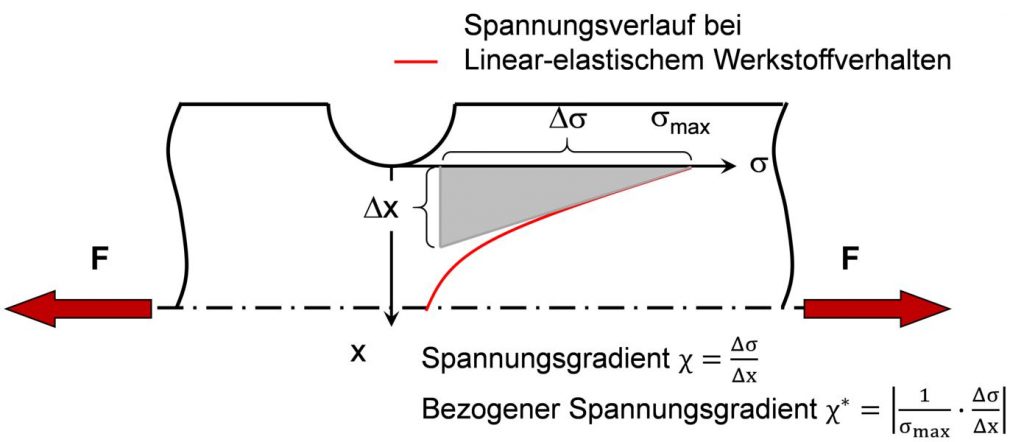
Definition des Spannungsgradienten
Der Spannungsgradient erklärt auch, dass ungekerbte biege- oder torsionsbelastete Bauteile auf Grund ihrer inhomogenen Spannungsverteilung eine höhere Schwingfestigkeit haben als ungekerbte zugbelastete Bauteile. Deshalb kommt ihm beim Betriebsfestigkeitsnachweis eine zentrale Rolle zu.
Nun aber zur eigentlich spannenden Frage: Wie berechne ich eigentlich den Spannungsgradienten aus meinen FEM Ergebnissen?
Für eine genaue Betriebsfestigkeitsberechnung ist die möglichste exakte Berechnung des Spannungsgradienten notwendig. Eine Berechnung des Spannungsgradienten aus FEM Ergebnissen kann aufwändig sein.
Praxistipp:
In einer ersten Berechnung kann der Spannungsgradient vernachlässigt werden. Damit wird ohne Stützwirkung gerechnet werden. Das Ergebnis liegt dann auf der sicheren Seite. Sollte der Festigkeitsnachweis so bereits erbracht sein, kann die Berücksichtigung der Stützwirkung und damit die Berechnung des Spannungsgradienten entfallen. Erst wenn der Nachweis nicht mehr erbracht werden kann, lohnt sich die Berechnung des Spannungsgradienten.
Für jeden Punkt, an dem ein Festigkeitsnachweis geführt werden soll, muss ein bezogener Spannungsgradient χ* ermittelt werden. In der Praxis erfolgt dies oftmals nur für die kritischen Stellen.

Vernetzung der Kerbprobe zur Berechnung des Spannungsgradienten aus der FEM
Zur Berechnung des bezogenen Spannungsgradienten im Nachweispunkt wird ein Stützpunkt definiert (siehe folgende Abbildung). Dafür wird ein Pfad durch den Nachweispunkt senkrecht zur Bauteiloberfläche festgelegt. Der Stützpunkt liegt dann auf dem Pfad in einem frei wählbaren Abstand Δx von der Bauteiloberfläche. Aus der Differenz
der Spannung im Nachweispunkt (der maximalen Spannung σmax) und der Spannung am Stützpunkt σStützpunkt berechnet sich der Spannungsabfall Δσ siehe folgende Abbildung.
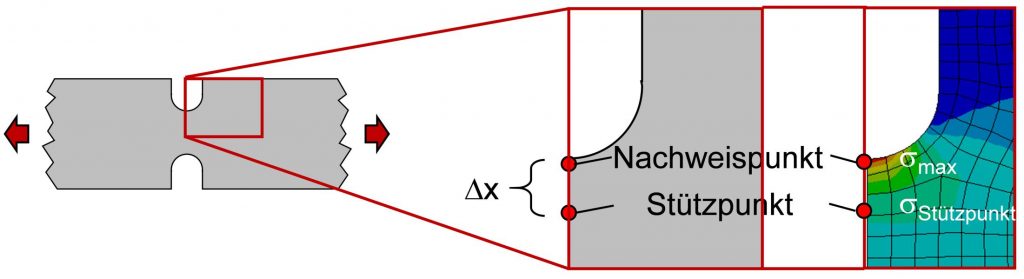
schematische Auswertung des Spannungsgradienten
Die Berechnung des bezogenen Spannungsgradienten erfolgt nach dieser Gleichung
Damit hängt der bezogene Spannungsgradient stark davon ab, wo der Stützpunkt gelegt wird. In den Richtlinien wird meist keine Angabe darüber gemacht wie dieser zu berechnen ist. Das Hauptproblem der Berechnung des Spannungsgradienten mittels FEM!
Hier finden Sie noch nützliche Hinweise zur Wahl der richtigen Elementtypen im FEM Netz.
Einflüsse auf den Spannungsgradienten
Der Spannungsgradient hängt im Wesentlichen von
- der Netzfeinheit
- der Auswerte Tiefe und
- der Auswerterichtung ab.
Einfluss der Netzfeinheit:
Grundsätzlich ist es erlaubt den Spannungsgradienten direkt an der Oberfläche aus dem ersten finiten Element abzulesen. In diesem Fall kann man die maximale Stützwirkung nutzen. Umsonst ist dies jedoch nicht! Je näher der Stützpunkt am Nachweispunkt liegt, umso feiner muss das FE-Netz sein, da die FE ja „nur“ ein Näherungsverfahren ist.
An der Geometrie von folgender Abbildung wurde eine Netzstudie durchgeführt um zu überprüfen, wann die Simulation konvergiert. Dazu ist das Netz der Kerbprobe schrittweise verfeinert worden. Der Radius wurde mit n=6...128 Elementen vernetzt. Ausgewertet wurde jeweils die maximale Spannung σmax und der bezogene Spannungsgradient χ* in einer Tiefe von 0,4 mm.
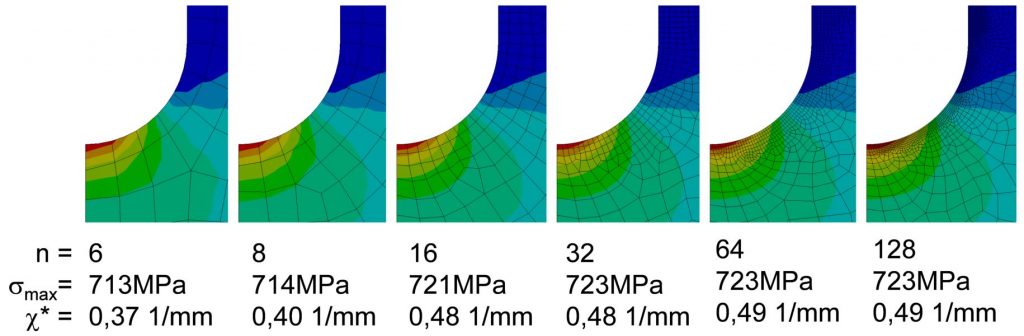
Netzstudie zur Ermittlung der richtigen Eelemntanzahl zur Berechnung des Spannungsgradienten aus FEM Ergebnissen
In den ersten drei Vernetzungen mit n=6, n=8 und n=16 Elementen über den Radius erkennt man, dass sich die Spannungen nur um etwa 1 Prozent unterscheiden: σmax = 713...721 MPa. Die Maximalspannungen konvergieren also bereits bei relativ groben Netzen.
Die Unterschiede der Spannungsgradienten dagegen unterscheiden sich um knapp 30 Prozent: χ* = 0,37 ... 0,48 1/mm. Ab etwa 16 Elementen über dem Radius hat auch der bezogene Spannungsgradient konvergiert.
Fazit: Das Netz ist also ausreichend fein, wenn der Kerbradius mit ca. 16 Elementen über dem 90° Radius vernetzt wird. Oder pragmatischer: wenn nur noch maximal ein Farbsprung in einem Element vorliegt (d.h. bei ca. 10 Farben in der Darstellung der FEM Ergebnisse unterscheiden sich die Spannungen in einem Element maximal um 10 %). Siehe dazu auch unseren Artikel zur Validierung von FEM Ergebnissen.
Einfluss der Tiefe der Auswertung
In folgender Abbildung ist der Einfluss der Auswertetiefe Δx auf die Auswertung des bezogenen Spannungsgradienten χ* dargestellt. Man sieht deutlich, dass der bezogene Spannungsgradient mit zunehmender Auswertetiefe abnimmt.
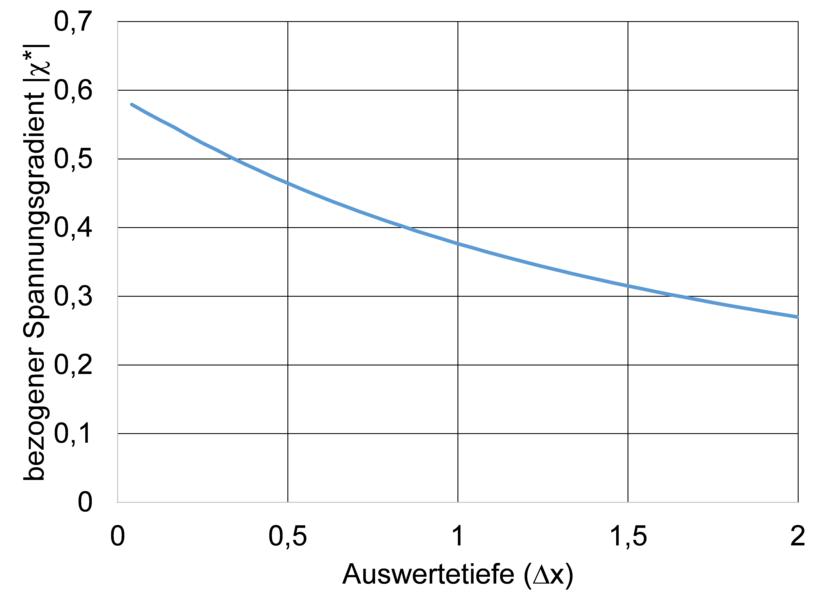
Einfluss der Auswertetiefe bei der Auswertung des Spannungsgradienten.
Wenn der bezogene Spannungsgradient im ersten Finiten Element bei Δx = 0,04mm bestimmt wird, erhält man einen bezogenen Spannungsgradienten von χ*0,04=0,581/mm. Wird bei Δx = 0,5mm ausgewertet, ergibt sich ein Wert von χ*0,5=0,465/mm. Beide Werte unterscheiden sich voneinander.
Um den Einfluss auf die Betriebsfestigkeit zu bewerten wird die Stützzahl nχ beispielhaft für einen S235 JR (Re = 235MPa, Rm = 420MPa) für die beiden bezogenen Spannungsgradienten berechnet. Da S235JR ein ferritischer Stahl ist, gilt nach unserem Buch Betriebsfestigkeit mit FEM:
nχ,0,04 =1,37
nχ,0,5 = 1,33
Der Unterschied zwischen den Stützzahlen beträgt nur knapp 3%. Deshalb können diese Unterschiede vernachlässigt werden. Ein gröberes Netz ist ausreichend.
Fazit: Die Auswertetiefe spielt keine große Rolle. Die Ergebnisse liegen auf der sicheren Seite, je größer die Auswertetiefe gewählt wird.
Einfluss der Auswerterichtung
Nicht immer ist es möglich den Auswertepfad genau senkrecht zur Bauteiloberfläche zu legen. Deshalb wird nachfolgend untersucht, wie groß der Einfluss ist, wenn der Auswertepfad um einen gewissen Winkel α von der idealen Position abweicht. Obige Abbildung zeigt das noch einmal schematisch.
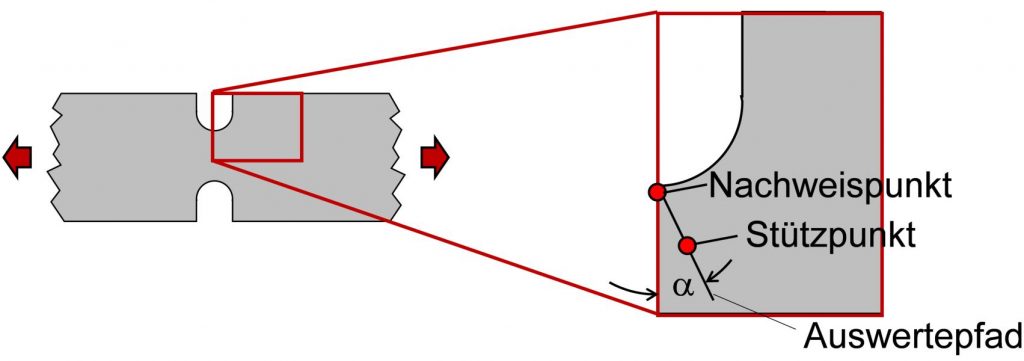
Einfluss der Auswerterichtung bei der Auswertung des Spannungsgradienten
Für Winkel von α = 1° .. 10° wird der bezogene Spannungsgradient in einer Tiefe von Δx=0,5mm für das Referenznetz berechnet. Die Ergebnisse zeigt die Tabelle:
| α | 1° | 2° | 5° | 10° |
| χ* | 0,465 1/mm | 0,465 1/mm | 0,464 1/mm | 0,461 1/mm |
Fazit: Für Abweichungen kleiner 10° sind auch die Unterschiede beim bezogenen Spannungsgradienten vernachlässigbar. Der Abstand zur Oberfläche oder die Netzfeinheit haben einen deutlich größeren Einfluss.
Auf den Punkt
- Die Stützwirkung spielt im genauen Betriebsfestigkeitsnachweis eine zentrale Rolle.
- Standardmäßig hängt die Stützwirkung vom bezogenen Spannungsgradienten ab.
- Der bezogene Spannungsgradient ist ein Maß für den Abfall der Spannungen von der Bauteiloberfläche ins Bauteilinnere.
- Für eine konservative Aussage kann der Spannungsgradient vernachlässigt werden.
- Der Spannungsgradient hängt ab von:
- Der Netzfeinheit
- Der Auswertetiefe
- Der Auswerterichtung
- Ein Netz ist ausreichend fein bei ca. 16 Elementen über dem Radius oder max. einer Farbe je Element.
- Die Auswertetiefe spielt keine große Rolle. Die Ergebnisse liegen auf der sicheren Seite, je größer die Auswertetiefe gewählt wird.
- Die Auswerterichtungen hat für Abweichungen kleiner 10° keinen signifikanten Einfluss auf den bezogenen Spannungsgradienten.
Weiterführende Informationen zur FKM Richtlinie und Wöhlerkurven
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Betriebsfestigkeit mit FEM
Das Seminar zur Betriebsfestigkeit gibt Ihnen einen guten Überblick über die Methoden der Betriebsfestigkeit und der FEM. Hier lernen Sie
✓ alle wichtigen Methoden kennen, um Ihre Bauteile robust auf die Betriebsfestigkeit auszulegen.
✓ Schweißverbindungen auszulegen.
✓ verstehen, welche Faktoren die Lebensdauer Ihrer Bauteile besonders stark beeinflussen.
✓ Grundlagen der Finite-Elemente-Ergebnisse (FEM) kennen, anzuwenden und zu interpretieren.
✓ Lastkollektive mit Hilfe der Rainflowzählung zu ermitteln.
✓ eine Wöhlerlinie für Ihre Bauteile rechnerisch abzuschätzen.
✓ Bauteillebensdauern mittels Schadensakkumulation zu berechnen.
✓ Dauerschwingfestigkeitsnachweise zu führen.
✓ die modernen Regelwerke wie die FKM Richtlinie zur Betriebsfestigkeitsbewertung kennen.
Seminare zur FKM Richtlinie:
Haben Sie Interesse an einer schnellen Anwendung und einem einfachen Einstieg in die komplexe FKM Richtlinie? Dann ist unsere Schulung zur FKM Richtlinie für Sie richtig.
Diese ist genau richtig für Sie, wenn Sie
✓ die FKM Richtlinie schnell anwenden möchten.
✓ Ihre FEM Ergebnisse bewerten wollen.
✓ die Hintergründe der FKM Richtlinie verstehen und üben wollen.
Weiterführende Literatur
 Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses führt Sie schnell und verständlich in die Versuche und die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auslegung Ihrer Bauteile auf die Dauerfestigketi oder Betriebsfestigkeit. Sie können dann einfach Wöhlerlinien für Ihre Bauteile berechnen.
Hilfreiche Software:

Wir haben basierend auf unserer jahrelangen Erfahrung, der Mitarbeit in den Forschungsgremien zur FKM Richtlinie und dem praktischen Arbeiten mit der Richtlinie FKMmadeEASY- die Excel-Software zur FKM Richtlinie entwickelt. Wir haben dabei speziell darauf geachtet, dass diese Software
✓ einfachst möglich bedienbar
✓ gut dokumentiert und nachvollziehbar sowie
✓ optisch ansprechend ist (es soll ja auch Spaß machen).
Überzeugen Sie sich selbst davon anhand der Testversion von FKMmadeEASY - die Excel-Software zur FKM Richtlinie

Sehr gute, ausführliche Erklärung des Themas. Die Untersuchung verschiedener Einflüsse wie Vernetzung oder Lage des Stützpunktes finde ich ebenfalls sehr gut und für die praktische Anwendung hilfreich. Es verschafft einem vorab ein Überblick, was man bei Änderung der Bedingungen zu erwarten hat. Das eigene “Herumprobieren” wird auf ein Minimum begrenzt.
Vielen Dank!
Hallo Herr Kaufmann,
vielen Dank für die nette Rückmeldung.
Ich wünsche Ihnen viel Spass bei der Betriebsfestigkeit
Stefan Einbock