Hexaeder, Tetraeder, linear, nichtlinear??? Was ist das richtige FEM Netz für die Betriebsfestigkeit?
Nutzen Sie auch die FEM um Ihre Bauteile zu simulieren? Dann kennen Sie sicherlich das Problem, das richtige FEM Netz zu finden. Dies ist insbesondere wichtig, wenn es darum geht, den Spannungsgradienten zu bestimmen. Wir zeigen Ihnen, wie Sie dies einfach erreichen und auf was Sie achten müssen.
Zuerst zeigen wir noch einmal, warum die Wahl des richtigen Netzes so wichtig ist. Danach sehen Sie anhand einer Netzstudie, wie das ideale Netz einer FEM für die Betriebsfestigkeit aussieht und am Ende erhalten Sie praktische Tipps für die Qualität des FEM Netzes.
Grundlagen FEM Berechnung
Häufig basiert eine Berechnung der Betriebsfestigkeit auf Kerbspannungen σmax. Dies können analytisch (also von Hand) aus den Nennspannungen σnenn und der Formzahl Kt berechnet werden:
σmax = Kt * σnenn.
Alternativ zur Berechnung der Kerbspannungen über den analytischen Weg, können diese auch mittels FEM berechnet werden. Bei linear-elastischer Berechnung ist das Ergebnis der FEM direkt die Kerbspannung.
Für die meisten Bauteile wird es nicht möglich sein, eine Formzahl zu definieren. Dann ist die einzige Möglichkeit Spannungen zu berechnen die Simulation, z. B. mit FEM. Um dies zu ermöglichen, wird die beliebig komplexe Bauteilgeometrie in einfache Elemente mit endlicher (finiter) Größe zerlegt (die Finiten Elemente).
Welche Arten von Finiten Elementen gibt es (linear, nichtlinear, Hexaeder, Tetraeder,...)?
In zweidimensionalen Modellen haben die Finiten Elemente die Form von Dreiecken und/oder Vierecken verwendet. In dreidimensionalen Modellen werden üblicherweise Tetraeder oder Hexaeder, Pyramiden mit 3 seitiger Grundfläche und Quader verwendet.
Neben der Form der Elemente unterscheidet man noch Elemente mit und ohne Seitenmittenknoten.
Alternative Bezeichnungen für diese Elemente sind: nichtlineare Elemente, quadratische Elemente oder Elemente mit quadratischer Ansatzfunktion. Es empfiehlt sich immer Elemente mit Seitenmittenknoten zu nutzen, da diese die Steifigkeit besser abbilden. Ganz allgemein lässt sich sagen, dass Elemente mit Seitenmittenknoten mehr Knoten haben, was bei gleicher Elementanzahl zu längeren Rechenzeiten führt. Gleichzeitig ist es aber so, dass Elemente ohne Seitenmittenknoten steifer sind, was wiederum bedeutet, dass für eine ausreichend feine Vernetzung mehr Elemente nötig werden.
Auf diese Weise kann jede beliebige Geometrie dargestellt werden. Je kleiner die Elemente sind und je mehr Elemente verwendet werden, desto genauer lässt sich die Geometrie darstellen.
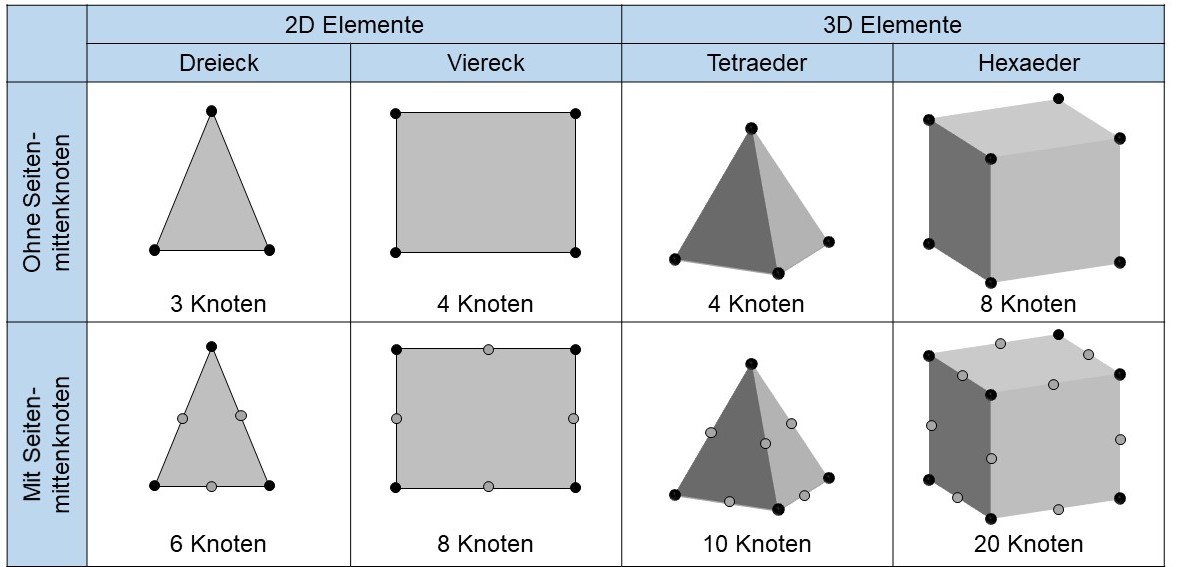
Arten von Finiten Elementen_Hexaeder_Tetraeder_linear
Wie ist das Vorgehen bei der FEM Berechnung und worauf muss man bei der FEM Vernetzung achten?
Bei der FEM Berechnungen werden aus den Randbedingungen Kräfte, daraus Knotenverschiebungen, dann Dehnungen, schließlich Spannungen und zuletzt Lebensdauern (genauer gesagt: die Spannungsgradienten oder die hoch belasteten Volumen) abgeleitet.
Je mehr Größen abgeleitet werden, umso größer muss die Sorgfalt bei der Netzgüte sein. Die oben dargestellte Kette zeigt, dass die Betriebsfestigkeit den höchsten Anspruch an die Netzgüte stellt.
Allerdings kennt jeder Anwender der FEM das Problem, dass der Aufwand hoch ist, gute FE-Netze zu generieren. Zusätzlich steigt natürlich auf die Berechnungsdauer mit zunehmender Netzfeinheit.
Es gilt also – wie so oft im Leben – ein Kompromiss muss her.
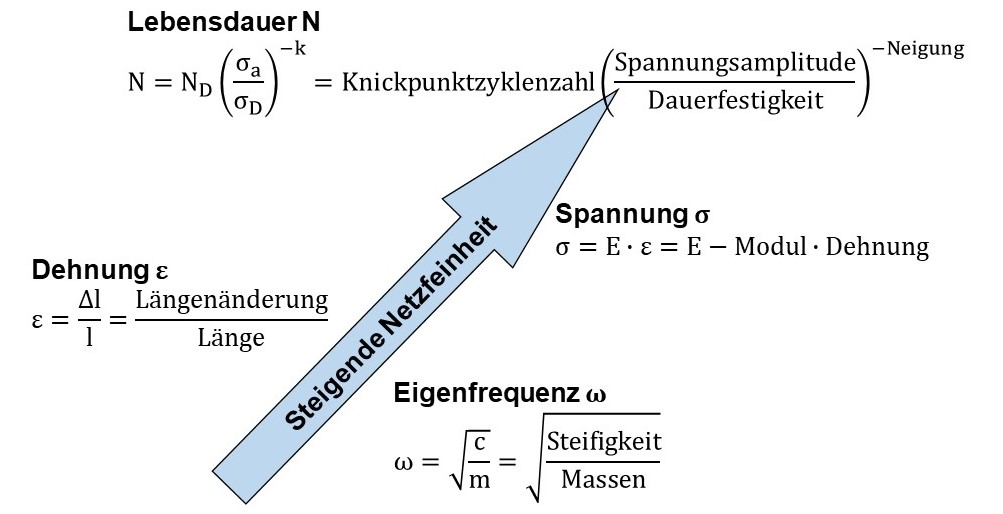
Abhängigkeit der Netzgüte bei der FEM von der Art der Berechnung
Um zu bewerten, ob die FEM Ergebnisse plausibel sind, haben wir noch 10 goldene Regeln zur Validierung der FEM Ergebnisse zusammengefasst: Link
Bei der FEM wird die Bauteilgeometrie in endlich große Elemente aufgeteilt. Daraus folgt, dass die Ergebnisse der FEM immer „nur“ eine Näherungslösung darstellen. Liegen keine Singularitäten vor (z. B. innenliegende Scharfe Kanten, Krafteinleitungen,…) dann gilt, dass mit steigender Netzfeinheit diese Näherungslösung immer näher am realen Ergebnis liegen wird.
Ab einem Grad der Netzfeinheit lohnt sich allerdings Steigerung der Elementanzahl nicht mehr. Man spricht dann davon, dass die Ergebnisse konvergiert sind (sich also bei weiterer Verfeinerung nur noch geringfügig ändern). Daraus stellen sich drei Fragen:
- Warum ist das FEM Netz für die Betriebsfestigkeit überhaupt so wichtig und
- Wann ist die FEM Netzqualität ausreichend?
- Welche Elemente muss ich denn verwenden?
Warum das FEM Netz wichtig ist – insbesondere für die Berechnung der Betriebsfestigkeit mit FEM
Ob für die Statische oder die zyklische Rechnung, das Netz der FE Berechnung muss ausreichend fein sein, um die Spannung korrekt abzubilden
Bei gemittelten Spannungsdarstellungen, wird die Spannung im Regelfall etwas unterschätzt, wenn die Vernetzung noch nicht ausreichend fein ist. Bei ungemittelten Spannungsdarstellungen wird diese im Regelfall etwas überschätzt. Daher ist es auch Sinnvoll sich sowohl die gemittelten als auch die ungemittelten Spannungsergebnisse anzusehen. Diese sollten möglichst identisch sein.
Während bei der statischen Rechnung noch etwas Toleranz gegeben werden kann, muss man für die zyklische Auslegung hohe Maßstäbe anlegen.
Der Grund dafür ist, dass durch die doppeltlogarithmische Natur der Spannungsbewertung die Abweichung verstärkt wird. Um dies zu veranschaulichen sehen wir uns die ursprüngliche Definition nach Basquin an.
N1/N2 = (σ1/σ2)-k
Mit dieser Beziehung können wir uns nun verdeutlichen, welchen Einfluss eine Spannungsvariation hätte.
Bei σ1/σ2 = 0,9 (also einer um 10 % unterschätzten Spannung) ergibt sich bereits eine um 69% verschätzte Lebensdauer (N1/N2=1,69) (unter Annahme einer Wöhlerlinienneigung von k = 5).
Daher sollte unser Netzfehler bei wenigen Prozent sein. Sollte ein potenzielles versagen des Bauteils sehr kritisch sein, ist daher immer eine Netzstudie zu verwenden.
Wann ist die FEM Netzqualität für die Betriebsfestigkeit ausreichend?
Als Daumenregel für die FEM Netzfeinheit gilt: Ein gutes Ergebnis erhält man, wenn man mit quadratischen Elementen auf einem Radius von 90° mindestens 5-6 Elemente hat. Die Netzfeinheit sollte allerdings auch in Tiefenrichtung noch gegeben sein!
Einige Vernetzer neigen dazu nur die Oberfläche fein zu vernetzen und die Tiefenrichtung zu vernachlässigen. Dies ist für Lebensdauerbewertungen nicht ratsam! Hier wird ja neben der Spannung selbst auch der Spannungsgradient (also der Abfall der Spannung in Tiefenrichtung) ausgewertet.
Ganz allgemein lässt sich sagen, dass Elemente mit Seitenmittenknoten mehr Knoten haben, was bei gleicher Elementanzahl zu längeren Rechenzeiten führt. Gleichzeitig ist es aber so, dass Elemente ohne Seitenmittenknoten steifer sind, was wiederum bedeutet, dass für eine ausreichend feine Vernetzung mehr Elemente nötig werden.
Nun kann man sich die Frage stellen, warum man nicht anstelle der quadratischen Elemente die linearen Elemente verwenden sollte (es ließe sich dadurch bei gleicher Elementanzahl die Knotenzahl reduzieren). Allerdings würden Sie mindestens 10 Elemente auf einen 90° Bogen benötigen um dieselbe Netzgüte zu erhalten. Bitte beachten Sie, dass für lineare Elemente lediglich Hexaeder, also Quaderförmige Elemente erlaubt sind. Lineare Tetraeder, also Dreiecke, verhalten sich zu steif und müssten extrem fein vernetzt werden um akzeptable Ergebnisse zu erzielen.
Daher der Rat für die richtigen FEM Elementtypen: Ganz generell würde ich in der Strukturmechanik zu quadratischen Elementen raten.
Sollten Sie sich unsicher sein, ob Ihre FEM gute Ergebnisse liefert, dann finden Sie hier 10 wichtige Hinweise zur Überprüfung der FEM Ergebnisse: https://www.einbock-akademie.de/validierung_fem/
Beweis der Aussagen zur Netzfeinheit:
Um die obigen Empfehlungen zu verifizieren wurde erneut eine einfache Netzstudie durchgeführt, welche die vorhandenen Empfehlungswerte bestätigt.
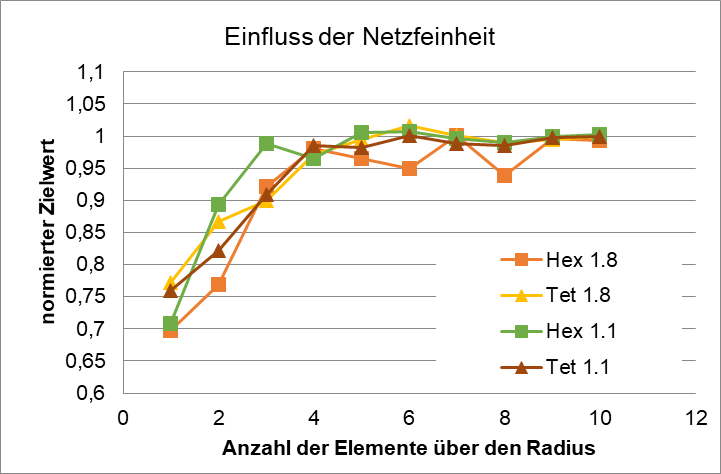
Notwendige Anzahl Elemente für die Betriebsfestigkeit (Netzstudie)
Wie Sie an Obenstehendem Diagramm erkennen können ist, ab 5 Elementen über dem Radius der Zielwert nahezu erreicht und aufgrund von nummerischen Schwankungen pendelt sich der Zahlenwert ein.
Untersucht wurden sowohl Hexaeder als auch Tetraeder (beide mit Seitenmittenknoten). Die Wachstumsrate in die Tiefe wurde auf 1.1 und 1.8 gesetzt. Dies bedeutet, dass ein Element mit einer 1mm Kantenlänge in Tiefenrichtung 1.1 mm, respektive 1.8 mm betragen darf.
Das nächste entsprechend auf 1.21 mm (1,1*1,1mm), respektive 3.24 mm (1,8*1,8mm), anwachsen darf bis, die gewünschte globale Elementgröße erreicht ist.
Zwischen Hexaedern und Tetraedern zeigt sich dabei kein sonderlich großer Unterschied ab etwa 4-5 Elementen über den Radius. Dies deckt sich mit den Erfahrungen der täglichen Praxis. Tetraeder -wie man in obiger Darstellung sieht- erzielen vergleichbare Ergebnisse, für den Preis von etwas mehr Elementen also auch einer höheren benötigten Rechenleistung.
Im Regelfall können Sie eine Struktur mit Hexaedern mit weniger Elementen bei derselben Ergebnisgüte vernetzen, der Aufwand in der Vernetzung ist jedoch ungleich höher!
Daher der Rat, immer mit Hilfe von Tetraedern mit Seitenmittenknoten zu vernetzen.
Warum verwenden Doktorarbeiten dann häufig Hexaeder bei FEM?
In Doktorarbeiten und wissenschaftlichen Studien werden Sie primär Hexaedervernetzungen finden. Dies hat meiner Meinung nach zwei Ursachen.
- Von der Theorie her sind Hexaeder tatsächlich etwas besser als Tetraeder, dieser Unterschied ist bei quadratischen Elementen zwar geringer ausgeprägt, ist bei linearen Elementen aber so eindeutig, dass lineare Tetraeder nicht verwendet werden sollten. Daher wird Netzen mit Hexaeder Elementen grundsätzlich unterstellt, dass diese qualitativ hochwertiger wären.
- Bei Doktorarbeiten ist es eher ein Ressourcen als ein Zeitproblem. Es ist manchmal durchaus sinnvoll mehrere Tage Arbeit in ein Netz zu investieren um damit, mit geringen Hardwareanforderungen, die Aufgabe bestmöglich zu erfüllen. Bei industriellen Anwendungen macht es jedoch deutlich mehr Sinn, entsprechend starke Hardware anzuschaffen, um die benötigte Ingenieurszeit zu reduzieren. Rechenhardware stellt den kleineren Kostenpunkt dar und die Bearbeitungszeit kann deutlich reduziert werden. Daher sind im Alltagsgeschäft Netze mit Tetraederelementen häufiger anzutreffen.
Welche Elemente muss ich denn verwenden? Und wie sehen dann die Spannungen im Bauteil aus?
Dargestellt in nachfolgender Abbildung ist die Vernetzungen eines Wellenabsatzes mit 8 Elementen über dem Radius. Es werden vier Varianten miteinander verglichen. Es werden immer Elemente mit Seitenmittenknoten verwendet. Die Vernetzung mit:
- Tetraedern und einer feinen Vernetzung in Tiefenrichtung (Tetraeder 1.1),
- Tetraeder und einer groben Vernetzung in Tiefenrichtung (Tetraeder 1.8)
- Hexaedern und einer feinen Vernetzung in Tiefenrichtung (Hexaeder 1.1),
- Hexaedern und einer groben Vernetzung in Tiefenrichtung (Hexaeder 1.8)
Ziel ist es den Einfluss der Vernetzung auch in Tiefenrichtung zu untersuchen.
Wir sehen, dass in allen Varianten die Spannungen an der Bauteiloberfläche vergleichbar und bereits recht gut auskonvergiert sind. Dies bestätigt die Aussage, dass problemlos mit Tetraeder Elementen gearbeitet werden kann.
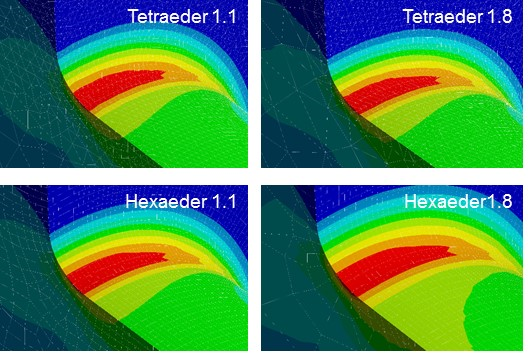
Einfluss der Netzqualität auf die Ergebnisse der FEM Berechnung
Wenn wir nun die Vernetzungen miteinander vergleichen, dann ist zu erkennen, dass die beiden Vernetzungen mit einer Wachstumsrate von nur 1.1, im Bild links zu erkennen eine wesentlich größere Anzahl von Elementen in Tiefenrichtung aufweisen als bei einer Wachstumsrate von 1.8. Dadurch wird die Rechenzeit höher.
Bei den Tetraedervernetzungen ist weiterhin zu erkennen, dass zumindest die erste Schicht von Elementen noch durch relativ feine Elemente gekennzeichnet ist. Bei den Hexaederlementen können bereits die Elemente in der ersten Lage vergleichsweise groß sein. Dadurch unterscheidet sich insbesondere bei groben Netzen der Verlauf der Spannung in die Tiefe deutlich. Vor allem Vernetzungen mit Hexaederelementen reagieren hier sensibel.
Wird nur die maximal auftretende Spannung betrachtet, so ist die Vernetzung in die Tiefe des Bauteils zweitrangig.
ABER: in der Betriebsfestigkeit wird aus dem Abfall der Spannungen ins Bauteilinnere der Spannungsgradient berechnet. Abhängig von diesem und dem Werkstoff (Link ) ermittelt man dann die Stützwirkung und hebt damit die Festigkeit an. Um den Spannungsgradienten zu ermitteln ist es also unbedingt nötig, das Bauteil auch im Inneren fein zu vernetzen.
Auf den Punkt: gute FEM Netze für die Betriebsfestigkeit
- Die FE-Methodik teilt ein komplexes Bauteil in kleine berechenbare Elemente endlicher Größe auf (die finiten Elemente).
- Eine Unterstützung durch Computer ist unbedingt erforderlich.
- Kostenlose Programme gibt es auch (siehe unseren Artikel: Link)
- Eine ausreichend feine Vernetzung ist notwendig, da sich die resultierenden Fehler bei der Berechnung der Spannungen stark auf die Lebensdauer auswirken.
- Verwenden Sie grundsätzlich Elemente mit quadratischer Ansatzfunktion). Diese werden mitunter auch als quadratische Elemente oder Elemente mit Mittelknoten bezeichnet.
- Bei einem Radius von 90°, benötigen Sie mindestens 5-6 Elemente.
- Es können sowohl Tetraeder als auch Hexaeder sein, für das Ergebnis spielt dies keine Rolle.
- Mit Tetraederelemente vernetzen Sie Ihr Bauteil deutlich einfacher und schneller bei gleicher Qualität.
- Beachten Sie, dass der Gradient in die Tiefe nicht zu groß wird. Eine Wachstumsrate von 1.1 bis 1.3 wird empfohlen.
- In kritischen Fällen kann eine Netzstudie erforderlich werden.
- Hinweise zur Überprüfung der FEM Ergebnisse: Link
Oder das Fazit von Erke Wang (Geschäftsführer von CADFEM) mit der Empfehlung zur Verwendung von Tetraederelementen:
Modellierst du noch, oder simulierst du schon?
