Wöhlerlinien nach dem Perlschnurverfahren auswerten
Wollen Sie die statistische Auswertungen von Wöhlerlinien selbständig durchführen? Vielleicht weil Sie die Wöhlerlinie für Ihren Festigkeitsnachweis nicht rechnerisch abschätzen können oder weil Ihnen die rechnerische Abschätzung zu ungenau ist? Hier erfahren Sie wie Sie mit Hilfe des Perlschnurverfahrens Wöhlerlinien statistisch auswerten und den Wöhlerversuch planen.
In diesem Artikel lernen Sie
- das Perlschnurverfahren kennen
- den Unterschied zwischen dem Perlschnurverfahren und dem Horizontenverfahren
- wie Sie den mittleren Verlauf der Wöhlerlinie statistisch auswerten
- worauf es bei der Versuchsplanung ankommt
- Praxistipps für die Planung und Auswertung kennen.
Inhalt:
Grundlagen
Die Ergebnisse eines Wöhlerversuches werden üblicherweise in ein doppellogarithmisches Netz eingetragen. Um den mittleren Verlauf der Wöhlerlinie zu bestimmen sind dann noch zwei Geraden einzuzeichnen, die den Zeitfestigkeitsbereich und den Bereich der Dauerfestigkeit beschreiben.
Zur Visualisierung der Streuungen wird noch ein Streuband angegeben. Dieses wird durch zwei zusätzliche parallele Wöhlerlinien für die Ausfallwahrscheinlichkeiten von 10% und 90% beschrieben. Die Berechnung des Streubandes ist nicht Gegenstand dieses Artikels.
Folgende Abbildung illustriert das Vorgehen anschaulich.
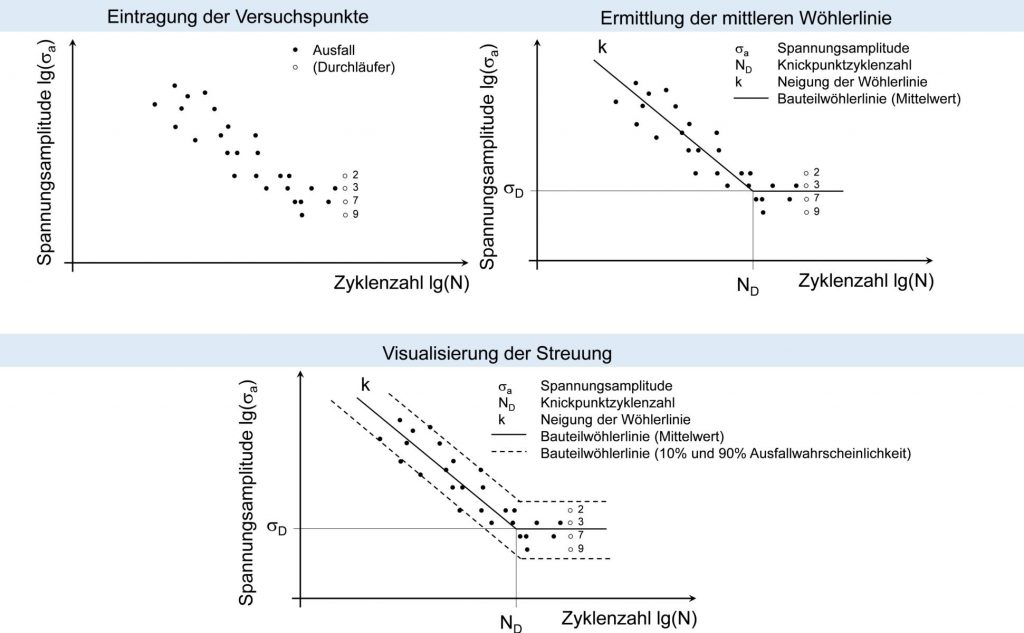
Drei Schritte zur Auswertung von Wöhlerlinien im Zeitfestigkeitsbereich (Perlschnurverfahren)
Der Wöhlerversuch
Die Betriebsfestigkeit ist ein empirisches Fachgebiet. Das bedeutet, dass viele Erkenntnisse auf der Interpretation von Versuchsergebnissen beruhen. Ein Beispiel dazu ist die experimentell ermittelte Wöhlerlinie. Im Wöhlerversuch wird die Spannungsamplitude variiert und für jede Spannungsamplitude wird so lange getestet, bis die Lebensdauer erreicht ist.
Die Versuchsergebnisse streuen. Als Ergebnis liegt also eine Datenpunktwolke und kein funktionaler Zusammenhang vor. Um in diese Datenpunktwolke eine Ausgleichsfunktion zu legen, die den Trend beschreibt werden Regressionsmethoden verwendet. Im Gegensatz zur typischen Regression wird in der Betriebsfestigkeit die Zyklenzahl (also der x-Wert) als Zufallsgröße gewählt.
Prinzipiell existiseren zwei Möglichkeiten (und beliebige Mischformen dieser beiden Möglichkeiten) um die Versuche durchzuführen.
- Das Perlschnurverfahren und
- Das Horizontenverfahren.
Vergleich Perlschnurverfahren und Horizontenverfahren
Im Falle des Perlschnurverfahrens wird für jede Spannungsamplitude (Lastniveau) nur ein Prüfling solange getestet bis dieser ausfällt.
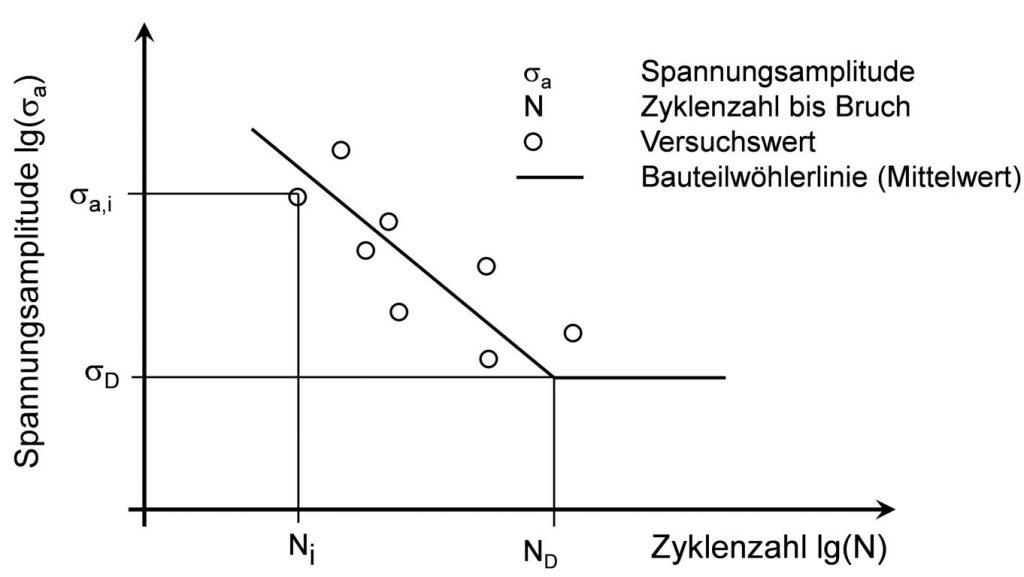
Das Perlschnurverfahren zur Ermittlung des Zeitfestigkeitsbereiches der Wöhlerlinie
Im Falle des Horizontenverfahrens werden für jede Spannungsamplitude (Lastniveau) mehrere Prüflinge bist zum Ausfall getestet.
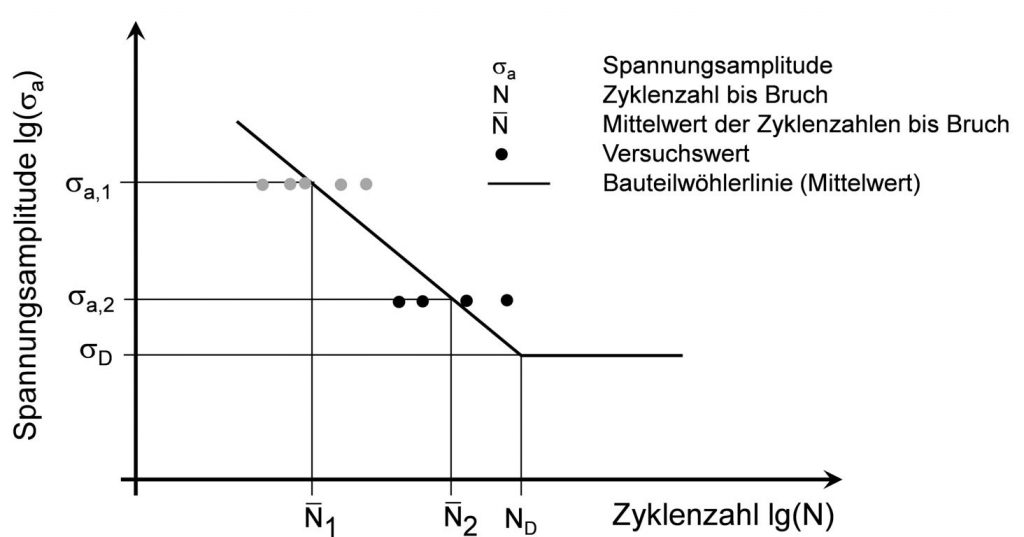
Das Horizontenverfahren zur Ermittlung der Zeitfestigkeit im Wöhlerversuch (schematisch)
Prinzipiell sind beliebige Mischformen in der Versuchsführung denkbar.
Vorteile des Perlschnurverfahrens:
- wenn wenig über den Werkstoff bekannt ist, denn dann kann der mittlere Verlauf der Wöhlerlinien mit relativ geringem Aufwand bestimmt werden.
- Sehr robust, da die Versuche über einen weiten Bereich der Wöhlerlinie platziert werden können.
- Setzt nur eine geringe Versuchsplanung voraus.
Nachteile des Perlschnurverfahrens:
- Streuungen können nur unter der Annahme einer von der Last unabhängigen Streuung ausgewertet werden
Vorteil des Horizontenverfahrens:
- Streuungen können in Abhängigkeit der Last (Spannungsamplitude) ermittelt werden
Nachteil des Horizontenverfahrens:
- Die Planung ist aufwändig, da die (beiden) Lasthorizonte möglichst weit voneinander entfernt platziert werden sollten. Dazu ist Vorwissen nötig. Es muss bekannt sein wo etwa die Wöhlerlinie liegen wird. Möglich ist dies z.B. mit der Berechnung der Wöhlerlinie nach der FKM oder aus Erfahrungen (z. B. aus Vorgängerprodukten).
Das Perlschnurverfahren
Die Wöhlerlinie lässt sich im doppellogarithmischen Netz als Gerade darstellen, siehe folgende Wöhlerlinie für Stahl:
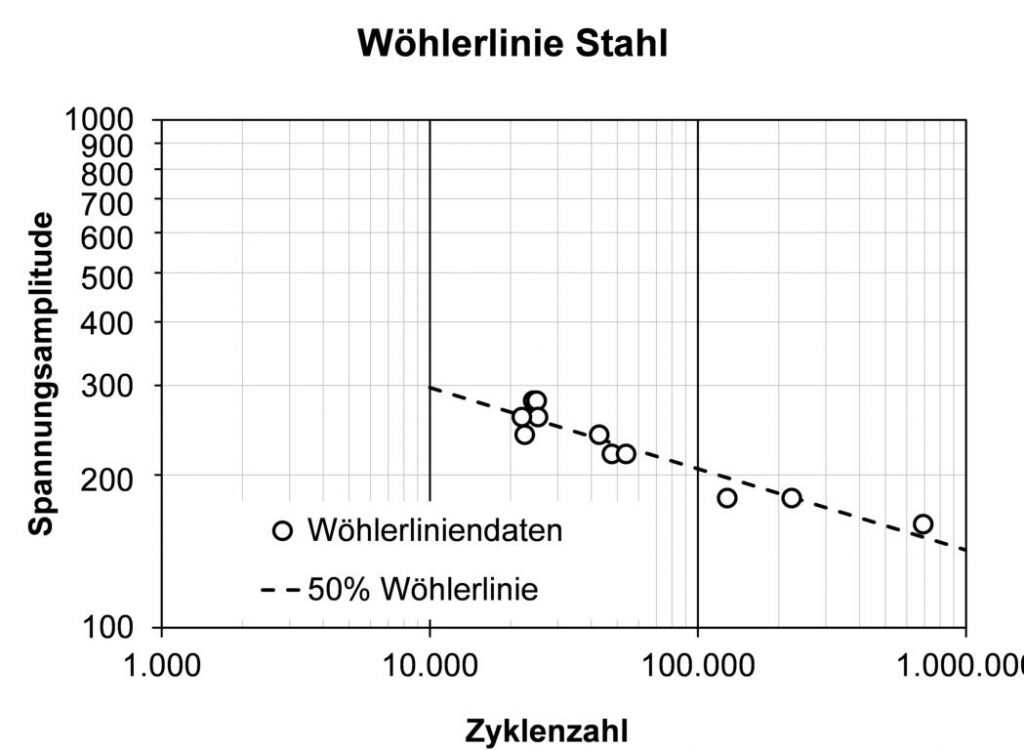
Beispiel einer Wöhlerlinie für Stahl
Die Gleichung ist:
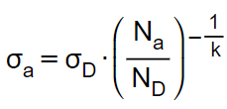
Darin ist
σa die Spannungsamplitude,
σD die Dauerfestigkeit,
Na die zur Spannungsamplitude σD gehörende Zyklenzahl
ND die Knickpunktzyklenzahl und
k der Neigungsexponent (dieser entspricht der Steigung).
Zur Ermittlung der Wöhlerlinie im Zeitfestigkeitsbereich wird der Wöhlerversuch in der Art geführt werden, dass auf mehreren Lasthorizonten (σa,i) Versuche bis zum Bruch gefahren werden. Üblich sind hier zwei Horizonte, siehe dazu auch obige Abbildung.
Jeder Lasthorizont kann anschließend unter Annahme der logarithmischen Normalverteilung separat bezüglich seines Mittelwertes und der Streuung ausgewertet werden.
Ermittlung der Neigung
Der mittlere Verlauf der Wöhlerlinie wird mittels Regressionsrechnung aus den Versuchsdaten bestimmt. Im Falle der Beschreibung der Wöhlerlinie wird in die folgenden Gleichungen als „x-Werte“ die erklärende Variable eingetragen, also die Spannungsamplituden σa,i. Als „y-Werte“ wird die zu erklärende Variable eingetragen, also die Zyklenzahlen Ni.
Dies steht im Gegensatz zur üblichen Vorgehensweise, da bei der Ermittlung der Wöhlerlinie immer die Spannungsamplitude variiert wird und sich die zugehörige Lebensdauer aus dem Versuch ergibt. Die Steigung (Parameter m) berechnet sich analog der Gleichung weiter unten. Da sich die Wöhlerlinie nur im doppellogarithmischen Netz als Gerade darstellen lässt, werden sowohl die x- als auch die y-Werte logarithmiert.
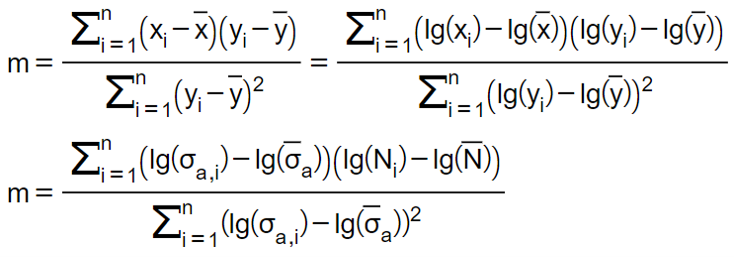
oder einfacher direkt mit dem Excel Formeln:
EXCEL: m = STEIGUNG(lg(N);lg(σa))
Der Achsenabschnitt berechnet sich nach:
![]()
oder mit Hilfe der Excel Formeln:
EXCEL: c = ACHSENABSCHNITT (lg(N);lg(σa))
mit den Mittelwerten:
EXCEL:
![]()
EXCEL:
![]()
wobei n die Anzahl der Versuche ist. Zur Ermittlung der Wöhlerlinie müssen Dauerfestigkeit σD, Knickpunktzyklenzahl ND und Neigungsexponent k bestimmt werden. Zwischen Neigungsexponent k und Steigung m besteht der Zusammenhang:
k= - m.
Ermittlung der Knickpunktzyklenzahl bei bekannter mittlerer Dauerfestigkeit
Ist die mittlere Dauerfestigkeit σD aus den Auswertungen von Dauerfestigkeitsversuchen (z.B. dem Treppenstufenversuch oder Berechnungen bekannt, dann kann die Knickpunktzyklenzahl ND) aus der der Geradengleichung y=mx+c berechnet:
y = mx+c
lg(N) = m∙lg(σ)+c
mit σ = σD kann dann Knickpunktzyklenzahl ND berechnet werden:
lg(ND) = m∙lg(D)+c
mit m und c aus dem obigen Gleichungen bei der Regression.
Ermittlung der mittleren Dauerfestigkeit bei angenommener Knickpunktzyklenzahl
Nicht immer liegen Dauerfestigkeiten vor. In diesem Fall kann auch eine Annahme für die Knickpunktzyklenzahl getroffen werden. Dies ist sicherlich der üblicherer Weg. Für die Knickpunktzyklenzahl gilt nach der FKM Richtlinie in der 7. Auflage* für Metalle
ND=106.
Die Dauerfestigkeit wird aus der Geradengleichung y=mx+c berechnet:
y = mx+c
lg(N) = m∙lg(σ)+c
mit ND = 106 und σ = σD kann dann die Dauerfestigkeit σD berechnet werden:
lg(ND) = m∙lg(σD)+c
σD = (ND/10c)1/m.
mit m und c aus dem obigen Gleichungen bei der Regression.
Hinweis: Die nach diesem Vorgehen ermittelte Dauerfestigkeit ist als Stützpunkt der Wöhlerlinie anzusehen. Für eine konservativere Auslegung kann mit ND=107 gerechnet werden. Für eine genaue experimentelle Ermittlung der Dauerfestigkeit sind spezielle Verfahren wie das Treppenstufenverfahren oder das Probitverfahren notwendig.
Praxistipp:
Allgemein gilt:
- Wenn wenig über den Werkstoff bekannt ist, dann sollte das Perlschnurverfahren die erste Wahl sein.
- Weichen die Ergebnisse von einer Geraden ab (z. B. zu hohe oder zu niedrige Horizonte, dann können diese aus der Auswertung entfernt werden)
Für die Versuchsplanung gilt:
- Für die Auswahl des ersten Versuchspunktes empfiehlt es sich die Wöhlerlinie nach z. B. der FKM Richtlinie in der 7. Auflage* zu berechnen und den ersten Versuch im Schwerpunkt der Wöhlerlinie bei N = 105 Zyklen zu platzieren.
- Versuche möglichst weit voneinander entfernt platzieren. Dann ist die Auswertung bezüglich der Neigung deutlich robuster. Gut ist, wenn der höchste Lasthorizont bei etwa N1 = 2*104 und der niedrigste bei N2 = 5*105 Zyklen liegt.
- Mit etwa 10 Proben kann der mittlere Verlauf der Wöhlerlinie gut experimentell bestimmt werden.
- Je besser die Versuchsvorbereitung, umso effizienter ist die Versuchsführung.
Für die Versuchsdurchführung gilt:
- Beginnen Sie mit Versuchen, die möglichst geringe Lebensdauern (ca. N = 105) aufweisen, da diese relativ schnell ein Ergebnis liefern. Denken Sie daran, dass zwischen einer Lebensdauer von N = 105 und N = 106 der Faktor 10 liegt! Dauert der erste Versuch drei Stunden, dann dauert der zweite Versuch bereits 30 Stunden!
- Arbeiten Sie sich dann von hohen Lasthorizonten zu den niedrigen Lasthorizonten durch.
Auf den Punkt:
- Das Perlschnurverfahren ist ideal, wenn Sie wenig über den Werkstoff oder das Bauteil wissen.
Der mittlere Verlauf der Wöhlerlinie:
- Mit Hilfe der Regression wird der mittlere Verlauf der Wöhlerlinie berechnet.
- Bei Wöhlerlinien werden quadratische Abweichungen in x-Richtung (Lebensdauerrichtung N) minimiert
Allgemein:
- Versuche möglichst weit voneinander entfernt platzieren. Dann ist die Auswertung bezüglich der Neigung deutlich robuster.
für die Auswahl des ersten Versuchspunktes empfiehlt es sich die Wöhlerlinie nach z. B. der FKM Richtlinie in der 7. Auflage* zu berechnen und den höchsten Lasthorizont bei N1 = 2*104 und der niedrigste bei N2 = 5*105 Zyklen zu wählen. - Beginnen Sie mit Versuchen, die möglichst geringe Lebensdauern (ca. N = 105) aufweisen, da diese releativ Schnell ein Ergebnis liefern. Denken Sie daran, dass zwischen einer Lebensdauer von N =105 und N =106 der Faktor 10 liegt! Dauert der erste Versuch drei Stunden, dann dauert der zweite Versuch bereits 30 Stunden!
Weiterführende Informationen zur Auswertung von Wöhlerversuchen
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren und Büchern. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Werkstoffkennwerte der Betriebsfestigkeit (für Simulation und Auslegung) einfach ermitteln und anwenden
Wollen Sie Ihre Versuche so kostengünstig wie möglich und mit der geringsten Anzahl an Versuchen durchfürhen? Dann ist evtl. unsere Wöhlerlinien auswerten und Versuche planen für Sie richtig.
Sie lernen hier,
- wie Sie Wöhlerversuche und Dauerfestigkeitsversuche mit geringst möglichem Stichprobenumfang durchführen
- Wöhlerlinien und Dauerfestigkeiten statistisch auszuwerten
- Ausreißer zu finden und mit Ausreißern umzugehen
- Versuche aus der Vergangenheit zu nutzen
- mit sehr geringen Stichprobenumfängen umzugehen
- Sicherheiten für Ihre Bauteilauslegung abzuleiten
- zwei Wöhlerlinien statistisch miteinander zu vergleichen
- einen kurzen Einstieg in die Betriebsfestigkeit kennen.
Weiterführende Literatur

Um Wöhlerkurven und Dauerfestigkeiten statistisch auszuwerten und zu planen, bietet sich außerdem unser Buch Statistik der Betriebsfestigkeit an.
dieses führt Sie schnell und verständlich in die Versuche und die Statistik Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auswertung von Versuchen der Betriebsfestigkeit wie Wöhlerlinien.
