Führen Sie auch Dauerfestigkeitsversuche durch und werten diese statistisch aus? Dieser Artikel zeigt eine Übersicht über die gängigsten Verfahren und wann diese nach der Wissenschaft (DIN50100 und Diss. Hr. Müller Link) angewandt werden. Das Treppenstufenverfahren nach Hück wird detailliert beschrieben.
In diesem Artikel lernen Sie,
- Wie Sie Ihre Dauerfestigkeitsversuche mit dem Treppenstufenverfahren nach Hück planen und auswerten
- Welche Verfahren es sonst noch gibt
- wann sich welches Verfahren am besten eignet.
Inhalt
Übersicht der Verfahren zu Dauerfestigkeitsauswertung
Für die Auswertung der Versuche im Dauerfestigkeitsbereich stehen verschiedene Verfahren zur Verfügung. Müller hat in seiner Dissertation Link umfangreich untersucht welche Auswerteverfahren die treffsichersten Ergebnisse liefern. Diese Ergebnisse sind auch in die DIN50100 eingflossen. Untersucht wurde das Treppenstufenverfahren und die Auswertung nach Hück, Maximum Likelihood, Deubelbeiss und Klubberg sowie das Probitverfahren und das Abgrenzungsverfahren.
Bei der Bewertung der Verfahren muss unterschieden werden, ob nur die Mittelwerte σD,50% oder auch die Streuungen (also die Standardabweichungen sσ ) ermittelt werden sollen. Für die Auswertung von Mittelwerten sind alle Verfahren geeignet. Die nötigen Stichprobenumfänge sind überschaubar. Anders sieht dies bei der Auswertung der Streuungen aus. Um hier treffsichere Aussagen liefern zu können, sind die erforderlichen Stichprobenumfänge teilweise sehr hoch.
Empfehlungen
Für die Auswertung der Dauerfestigkeit werden folgende drei Verfahren empfohlen:
- Das Treppenstufenverfahren mit der Auswertung nach Hück liefert neben einer einfachen und robusten Versuchsführung die zuverlässigsten Ergebnisse bei der Auswertung des Mittelwertes.
- Das Abgrenzungsverfahren ist insbesondere für die Auswertung von Streuungen bei kleinen Stichprobenumfängen (n < 40) anzuwenden. Im Vergleich zum Treppenstufenverfahren liefert es vergleichbare Ergebnisse bei der Mittelwertauswertung. Die Versuchsplanung ist jedoch aufwändiger.
- Trotz der schlechteren statistischen Ergebnisse wird außerdem noch auf das Probitverfahren eingegangen, da es eine hohe Verbreitung aufweist.
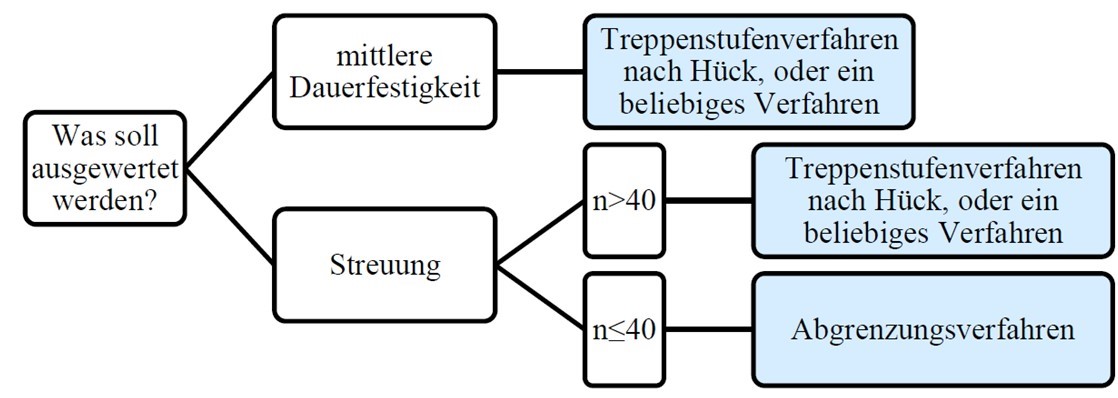
Empfehlung für Verfahren zur experimentellen Auswertung der Dauerfestigkeit
Das Treppenstufenverfahren nach Hück
Das Treppenstufenverfahren ist das am häufigsten eingesetzte Verfahren zur Auswertung von Versuchen im Bereich der Dauerfestigkeit. Die Versuchsführung und -auswertung des Treppenstufenverfahrens erfolgt in drei Schritten, die in folgender Abbildung dargestellt sind:
- Festlegung der Treppenstufen
- Versuchsführung inkl. Auswahl des Starthorizontes
- Auswertung der Ergebnisse
Die nötigen Randbedingungen
für den Einsatz des Treppenstufenverfahrens sind:
- Keine, wenn nur die mittlere Dauerfestigkeit ausgewertet werden soll.
- 40 Prüflinge, wenn auch die Streuung ausgewertet werden soll.
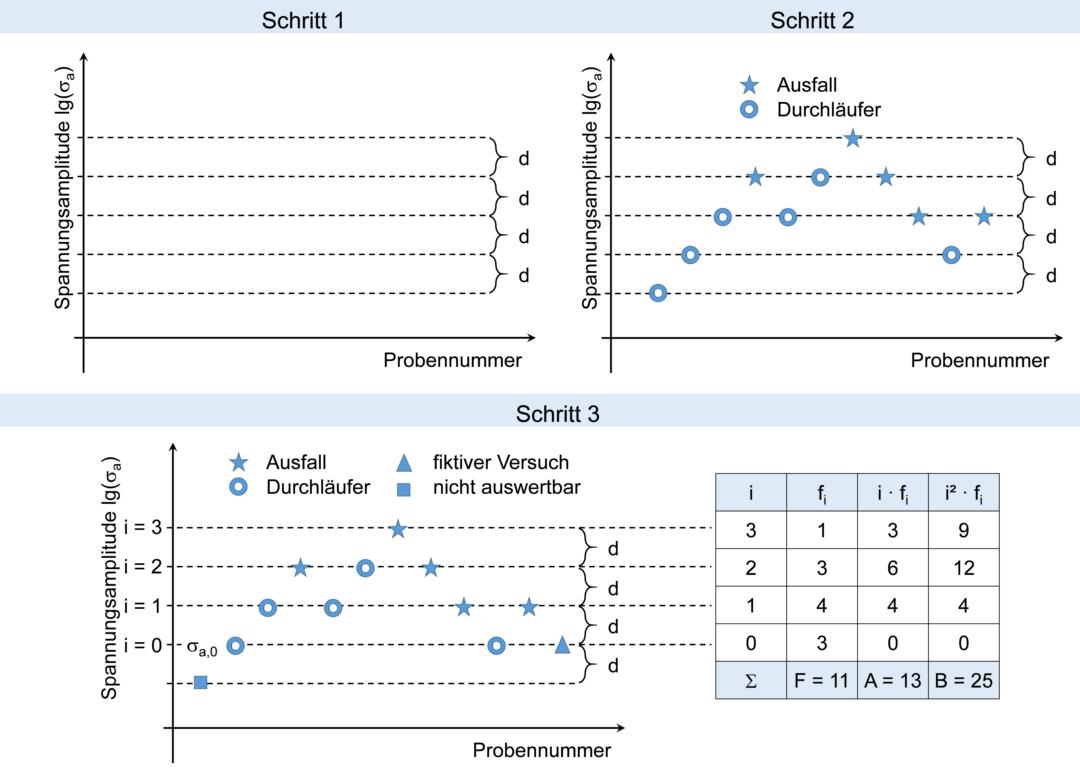
Drei Schritte des Treppenstufenverfahrens nach Hück zur Auswertung der Dauerfestigkeit
Schritt 1: Festlegung der Treppenstufen
Als erste Laststufe wird häufig die rechnerisch abgeschätzte Dauerfestigkeit σD* gewählt. Die Treppenstufen (oder auch Lasthorizonte) sollen alle den gleichen Abstand zueinander haben. Dieser Abstand wird als Stufensprung d bezeichnet. Da Wöhlerversuche immer im doppellogarithmischen Netz dargestellt werden, bedeutet dies, dass der logarithmische Stufensprung lg(d) zwischen zwei Spannungsamplituden gleich ist:
lg(d) = lg σa,i - lg σa,i+1 = lg(σa,i/σa,i+1) = konstant = lg(σa,i/σD*)
σa,i = σD* · di
mit
i = ..., -3, -2, -1, 0, 1, 2, 3, ...
σD* = abgeschätzte Dauerfestigkeit (z.B. mittels FKM-Richtlinie)
d = Stufensprung
σa,i = i-te Laststufe
Wird der Stufensprung zu groß gewählt, dann wird die Aussage zu ungenau, da zu wenige Stufen ausgewertet werden können. Bei einer zu kleinen Wahl des Stufensprungs wird der Versuchsaufwand zu groß. Eine gute Wahl des Stufensprungs ist getroffen, wenn für das Verhältnis aus der zu erwartenden Standardabweichung s zum logarithmischen Stufensprung lg(d) gilt
lg(d) = sσ ≈ 0,03...0,06.
Da die Standardabweichung vor dem Versuch nicht bekannt ist, muss diese aus Erfahrungswerten möglichst gut geschätzt werden. Dazu bieten sich entweder die Werte nach Haibach (vgl. Link) an oder eigene Werte aus vorangegangenen Versuchen.
Durch Einsetzen der beiden Gelichungen ineinander und Umformen kann der Zusammenhang zwischen der Laststufe σa,i und dem Stufensprung d, bzw. der Standardabweichung sσ berechnet werden:
lg(d) = sσ = lg(σa,i/σD*)
10sσ = σa,i/σD*
σa,i = σD* · 10sσ
mit i = ..., -3, -2, -1, 0, 1, 2, 3, ...
Schritt 2: Versuchsführung des Treppenstufenverfahrens nach Hück
Der Startwert ist der erste Lasthorizont (die erste Spannungsamplitude), auf dem ein Versuch durchgeführt wird. Dieser kann beliebig gewählt werden. Abhängig vom Ergebnis wird der nächste Lasthorizont gewählt. Handelt es sich um einen Ausfall, dann wird der nächste Lasthorizont um den Stufensprung niedriger gewählt. Trat dagegen ein Durchläufer auf, dann wird auf dem nächst höheren Lasthorizont geprüft (vgl. dazu obige Abbildung). Das Ergebnis ist dann die Treppenstufenfolge.
Eine große Stärke des Treppenstufenverfahrens ist, dass mit beliebigen Startwerten begonnen werden kann. Der Versuch wird sich automatisch um die Dauerfestigkeit zentrieren. Das Verfahren ist also sehr robust. Je näher der Startwert σD* an der wahren Dauerfestigkeit σD liegt, umso weniger Versuche sind nötig. Deshalb lohnt es sich, den Startwert gut zu wählen. Dazu kann entweder auf Erfahrungswerte aus früheren Versuchen zurückgegriffen werden, oder die Dauerfestigkeit wird rechnerisch abgeschätzt. Hier bietet sich beispielsweise die FKM-Richtlinie an.
Schritt 3: Versuchsauswertung
Für die Versuchsauswertung wird die Treppenstufenfolge aufbereitet (siehe obige Abbildung). Zum einen werden am Anfang der Treppenstufenfolge (dem Anschnitt) alle Versuche gestrichen, die bei der weiteren Versuchsführung nicht noch einmal auftreten. Zum anderen wird an das Ende der Treppenstufenfolge noch ein fiktiver Versuch angehängt. Dieser fiktive Versuch ist der Lasthorizont, welcher als nächster geprüft worden wäre. Möglich ist dies, da die Versuchsauswertung nicht nach Ausfall oder Durchläufer unterscheidet.
Alle auswertbaren Lasthorizonte werden aufsteigend nummeriert. Begonnen wird bei dem niedrigsten auswertbaren Lasthorizont ist σa,0 mit i = 0. Für jede der auswertbaren Lasthorzonte wird die Anzahl der Versuche fi gezählt und daraus die Hilfsgrößen F, A und B berechnet:
F = ∑ fi
A = ∑ i · fi
B = ∑ i² · fi
Die Dauerfestigkeit
Die mittlere Dauerfestigkeit σD,50% wird mit Hilfe der Hilfsgrößen F und A nach obigen Gleichungen , dem Stufensprung d sowie dem niedrigsten auswertbaren Lasthorizont σa,0 berechnet:
lg σD,50% = lg σa,0 + A/F · lg d
σD,50% = 10lg σD,50% = 10lg σa,0 + A/F · lg d = σa,0 · dA/F
Die Standardabweichung (Streuung)
Um die logarithmische Standardabweichung sσ zu berechnen wird aus den Hilfsgrößen F, A und B nach den obigen Gleichungen eine Hilfsvarianz kH ermittelt:
wenn (F · B - A²) / F² ≥ 0,5, dann: kH = (F · B - A²) / F²
wenn (F · B - A²) / F² < 0,5, dann: kH = 0,5
mit
a = 4,57949 · F-0,88952
b = 7,23555 · F-0,40523
liefert Müller Näherungsgleichungen zur rechnerischen Auswertung der Standardabweichung sσD des Versuches mit der Hilfsgröße F und der Hilfsvarianz kH :
wenn kH = 0,5, dann: sσD = 0,5 · lg d
wenn kH ≠ 0,5, dann: sσD = lg d · 10a · kHb.
In der Originalarbeit von Hück wird ein Diagramm angegeben, welches die auf den logarithmischen Stufensprung lg d bezogene logarithmische Standardabweichung sσD in Abhängigkeit der Hilfsvarianz kH und der Anzahl der auswertbaren Versuche F darstellt. Nach diesem Diagramm sind jedoch einige Versuchsreihen für kleinere Stichprobenumfänge (n < 20) nicht auswertbar. Da diese Stichprobenumfänge bei Betriebsfestigkeitsversuchen auf Grund der hohen Kosten durchaus vorkommen können, wird eine Alternative benötigt. Diese liefert Müller mit der angegebenen Gleichung. Dieser Vorschlag ist für Stichprobenumfänge von 10 ≤ n ≤ 100 sehr treffsicher.