Plastische FEM Berechnungen gehören mittlerweile zum Standard in der Simulation. Am Beispiel der kostenlosen FEM Software Salome Meca zeigen wir Ihnen wie Sie eine plastische FEM Berechnung sicher und einfach durchführen können!
In diesem Artikel lernen Sie
- eine plastische FEM Berechnung durchführen
- die kostenlose FEM Software Salome Meca noch besser kennen
- wie Sie die richtigen Einstellungen in Salome Meca für eine plastische FEM Berechnung wählen
- verstehen, was der Solver in der FEM eigentlich überhaupt macht und warum die plastischen FEM Berechnungen manchmal so schwierig sind
Inhalt
1 Motivation
Dieser Artikel ist eine Fortsetzung des Artikels zur Berechnung der plastischen Stützzahl nach der FKM Richtlinie für einen statischen Festigkeitsnachweis. In diesem Artikel fokussieren wir uns darauf, wie eine elastisch-plastische FEM Berechnung mit Hilfe der kostenlosen FEM Software Salome Meca durchgeführt werden kann.
Das hier beschriebene Vorgehen basiert auf dem statischen FEM Nachweis, den wir in unserem kostenlosen eBook zur FEM Berechnung mit Salome Meca beschrieben haben. Dieses eBook beinhaltet auch wertvolle Hinweise zur Installation der Software. Am besten Sie laden sich dieses eBook herunter und führen dann die darin beschriebenen Schritte für den linearen Nachweis aus.
In diese Artikel zeigen wir Ihnen dann, wie Sie ausgehend von diesen Berechnungen Ihr FEM-Modell anpassen, um eine plastische FEM Berechnung durchzuführen.
2 Unterscheide lineares und nichtlineares Material
Das normale Materialverhalten beschreiben wir Ingenieure durch die Spannungs-Dehnungs-Kurve. Folgende Abbildung zeigt ein typisches Spannungs-Dehnungs-Diagramm für einen duktilen Werkstoff (graue Kurve).
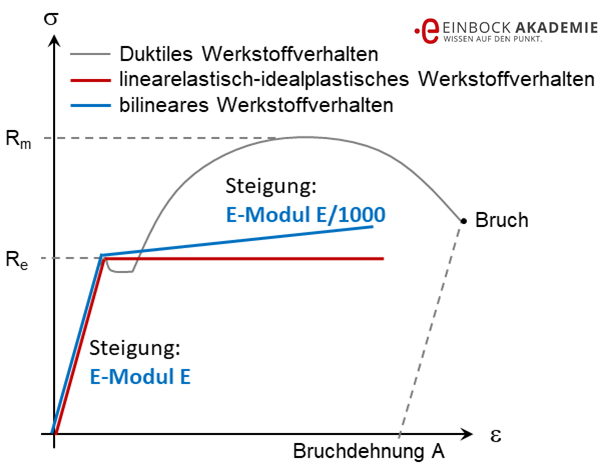
Darstellung unterschiedlicher plastischer Materialmodelle für die FEM Berechnung
Hierein sieht man, dass sich Spannung und Dehnung bis zur Streckgrenze linear verhalten. Oberhalb der Streckgrenze ist dieser Verlauf deutlich nichtlinear. Das Material plastifiziert.
Dabei wird aus Gründen der Einfachheit und der Robustheit versucht, dieses Materialverhalten so einfach wie möglich zu beschreiben. Die einfachste Möglichkeit ist die Annahme, dass es keine Plastifizierung gibt. Deshalb wird in diesem Fall das Material nur durch den E-Modul also lineares Material modelliert.
Für plastische FEM Berechnungen muss ein plastisches Materialmodell vorgegeben werden. In obiger Abbildung sind zwei Möglichkeiten angegeben:
- linearelastisch-idealplastisches Werkstoffverhalten (ohne Verfestigung)
- bilineares Werkstoffverhalten (mit linearer Verfestigung).
Daneben gibt es aber auch noch eine weitere Möglichkeit:
- multilineares Werkstoffverhalten (die Verfestigung wird mit mehreren Geradenstücken angenähert).
Das linearelastisch-idealplastische Werkstoffverhalten wird z. B. bei der Berechnung der plastischen Stützzahl nach der FKM Richtlinie angenommen. Für eine bessere Konvergenz der Simulation wird von diesem leicht abgewichen und ein bilineares Werkstoffverhalten mit einer sehr flachen Steigung angenommen.
In der Betriebsfestigkeit wird fast ausschließlich mit den linearen Werkstoffverhalten gearbeitet. Die wichtigste Ausnahme ist die Berechnung der plastischen Stützzahl beim statischen Festigkeitsnachweis z. B. nach der FKM Richtlinie, hier wird mit einem bilienaren Werkstoffverhalten gerechnet. Darum fokussiert dieser Artikel auf das bilineare Werkstoffverhalten.
3 Grundlagen
Eine lineare FEM Berechnung setzt die folgenden Eingaben voraus (diese sind detailliert in dem kostenlosen eBook zur Anwendung von Salome Meca beschrieben).
- Einlesen der Bauteilgeometrie
- Erstellung des Netzes
- Aufbau des FEM Modells (Netz, Randbedingungen, Belastungen, Materialmodell, Art der Finiten Elemente)
- Auswahl des richtigen Gleichungslösers
- Festlegung der Ergebnisdatei
- Berechnung des FEM Modells
- Auswertung der Ergebnisse
Für eine plastische FEM Berechnung werden zusätzlich noch folgende (detailliertere Daten benötigt):
- Netz optimieren (optional!)
- Anpassung der Materialdaten
- Angaben zur Steuerung des Gleichungslösers
- Anpassung der nichtlinearen Simulation.
4 Anpassung des linearen FEM Modells
Führen Sie am besten zuerst die linearelastische FEM Berechnung mit Salome Meca wie im kostenlosen eBook beschrieben durch. Anschließen sind nur noch die folgenden Anpassungen des linearen Modells notwendig.
4.1 Netz optimieren
Optional ist die Optimierung des FEM Netzes. Dieses hat zum Teil sehr kleine und damit sehr viele Elemente. Deshalb kann die Rechenzeit etwas hoch sein.
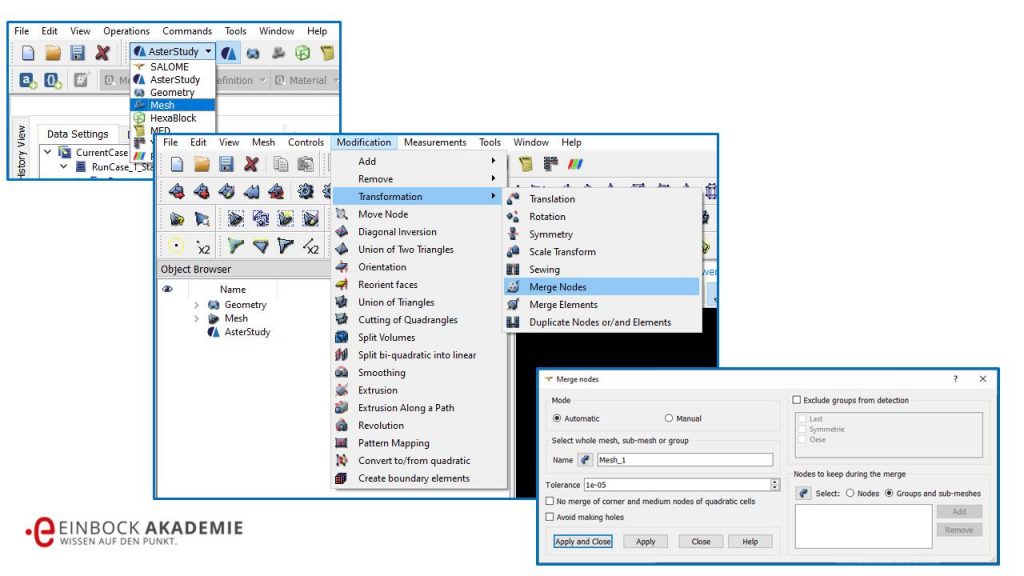
Einstellungen der Netzfeinheit zur Verringerung der Elementanzahl in Salome Meca
Gehen Sie dazu in den Netz Modul (siehe linkes Bild). Dann öffnet sich der Netz Modul und hier können Sie über das Menü „Modification -> Transformation -> Merge Nodes“ (siehe mittleres Bild) Knoten zusammenführen. Es öffnet sich dann das Fenster „Merge Nodes“ (siehe rechtes Bild). In diesem Fenster können im Feld „Tolerance“ Vorgaben gemacht werden, in welcher Größe Knoten zusammengeführt werden sollen. Der Wert gibt die Größe des Elementes in der gewählten Einheit an. WICHTIG: Arbeiten Sie sich in kleinen Schritten vor und bestätigen Sie die Auswahl mit „Apply“. Erscheint die Nachricht „There are no nodes to merge“, dann können Sie einen größeren Wert z. B: 1e-3 eingeben. Fahren Sie solange fort, bis eine Anzeige erscheint: „xx groups of nodes successfully merged“. Wenn Ihnen diese Anzahl genügt, dann bestätigen Sie die Auswahl mit „Apply and Close“. Falls nein, fahren Sie mit der Verfeinerung fort.
4.2 Anpassung der Materialdaten
Im Unterschied zur linearelastischen Berechnung muss das Materialmodell angepasst werden. Es wird ein bilineares Materialmodell angenommen. Dieses ist durch zwei Kennwerte eindeutig beschrieben:
- Den Tangentenmodul (die zweite Steigung) E* = 211.4 MPa.
- Die Streckgrenze Re = 900 MPa.
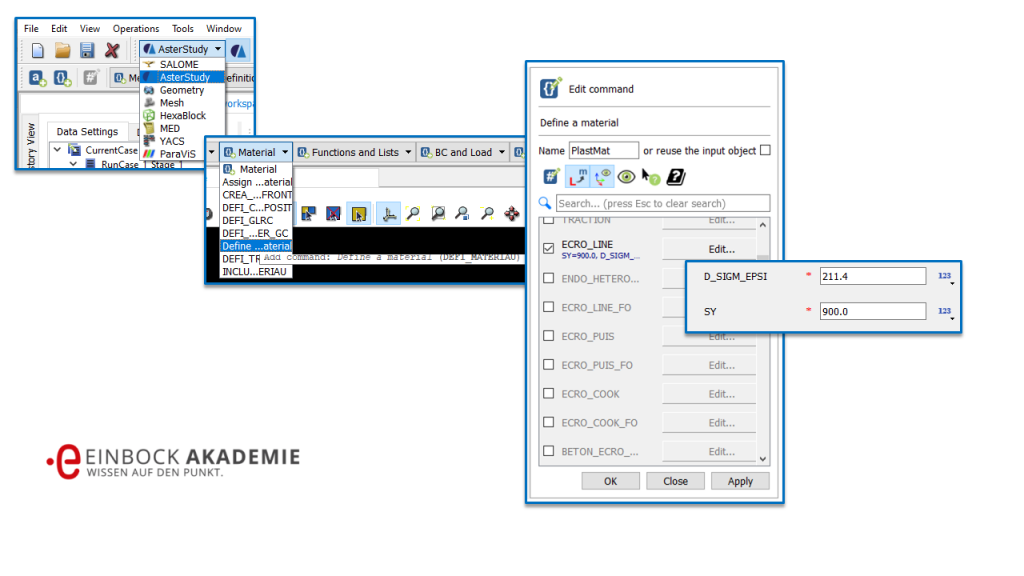
Anpassungen der Kennwerte für das bilineare plastische Materialmodell in der FEM
Die Anpassung der Materialdaten geschieht im Modul AsterStudy (siehe linkes Bild obiger Abbildung). Dann wird das über „Material -> Define a Material“ (siehe mittleres Bild) das Menü zur Definition eines neuen Materials geöffnet (siehe rechtes Bild). Hier wird ein neuer Name vergeben (PlastMat) und das gewünschte Material Modell gewählt („ECRO_LINE“). Hinweis: In Salome Meca sind dutzende Materialmodelle bereits vorgesehen. ECRO_LINE ist die Bezeichung für das bilineare Materialverhalten (siehe hier die Hilfe Datei zu den Salome Meca Materialmodellen).
Über den Button „Edit“ müssen noch die beiden Kennwerte
- Tangentenmodul E* = D_SIGM_EPSI = 211.4 MPa und
- Streckgrenze Re = SY = 900 MPa
Gewählt werden.
WICHTIG: Außerdem muss noch das linearelastische Materialmodell zusätzlich vorgegeben werden. Dazu wird der Haken im selben Menü bei „Material“ gesetzt und das lineareleastische Material S42CrMo4 gewählt.
Anschließend weisen wir das Material noch der Geometrie des Hakens zu.
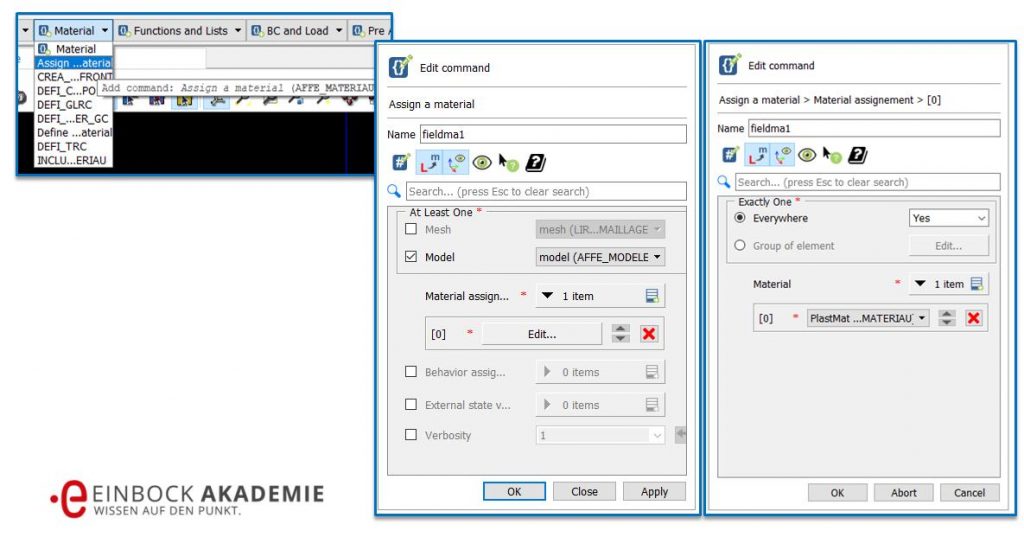
Zuweisung des Materials zur Geometrie im FEM Modell
Dafür selektieren wir „Material -> Assign Material“, setzen im sich öffnenden Menü den Haken bei „Model“ und klicken bei „Material assignment“ das Symbol ganz rechts. Jetzt können wir auf „Edit“ drücken (siehe mittleres Bild). Es öffnet sich ein zweites Menü (siehe rechtes Bild). In diesem weisen wir jedem Element („Everywhere“) die beiden Materialien (Linearelastisch -> S43CrMo4 und plastisch -> PlastMat) zu und bestätigen mit OK.
4.3 Randbedingungen festlegen
Nachdem die Materialeigenschaften festgelegt wurden, können jetzt die Randbedingungen definiert werden. Diese sind in unserem Fall dieselben, wie bei der Berechnung mit dem linearen Materialverhalten. Deshalb werden die Randbedingungen vom ursprünglichen Modell übernommen.
4.4 FEM Analyse durchführen
Nachdem wir jetzt das eigentliche FEM Modell bestehend aus dem Netz, den richtigen Elementen für eine strukturmechanische Berechnung, den Randbedingungen (Symmetrie, Festhaltung und Kraft) und dem Material haben, können wir mit der eigentlichen Berechnung beginnen.
4.5 Anpassung des Gleichungslösers
Der Gleichungslöser (Solver) zur Berechnung nichtlinearer Probleme (Materialplastizität) benötigt drei wesentliche Einstellungen. Dazu finden sie im nächsten Abschnitt die theoretischen Grundlagen.
Im zweiten Abschnitt dieses Kapitels wird gezeigt, wie in Salome Meca Funktionen festgelegt werden, um diese Einstellungen des Solvers zu steuern. Außerdem werden die Einstellungen beschrieben.
Abschließend werden im dritten Abschnitt die definierten Funktionen dem Solver zugewiesen.
4.5.1 Theoretische Grundlagen
Der Solver von Salome-Meca benötigt für die Berechnung der Plastizität drei Eingaben:
- Definition einer fikitven Zeitachse für die Lastschrittsteuerung
- Die Zeitschrittinkrementierung
- Festlegung, wie die Last verkleinert wird, falls keine Konvergenz vorliegt
Zu 1: Definition einer fikitven Zeitachse für die Lastschrittsteuerung
In diesem Schritt wird eine fiktive Zeitachse (x-Achse) für die folgenden zwei Funktionen festgelegt. Da Materialnichtlinearitäten nicht zeitabhängig sind, ist diese Zeitachse eine rein fikitve Größe. Deshalb wird dieser Parameter auch gerne als quasi-statische oder Pseudo-Zeit bezeichnet. Üblicherweise wird die Zeit von 0 Sekunden bis zu einer Sekunde vorgegeben.
Zu 2: Die Zeitschrittinkrementierung
Bei der Zeitschrittsteuerung wird festgelegt in wie vielen Schritten die Last aufgebracht wird. Im Gegensatz zu linearen Problemen kann bei nichtlinearen Problemen nicht direkt auf die Lösung / das Ergebnis geschlossen werden. Es sind dazu mehrere Schritte notwendig. Deshalb ist es einfacher zu einer Lösung zu kommen, je kleiner die Lastschritte gewählt werden, der Grad der Nichtlinearität sinkt (siehe auch folgende Abbildung).
Üblich sind hier etwa 10..100 Lastschritte.
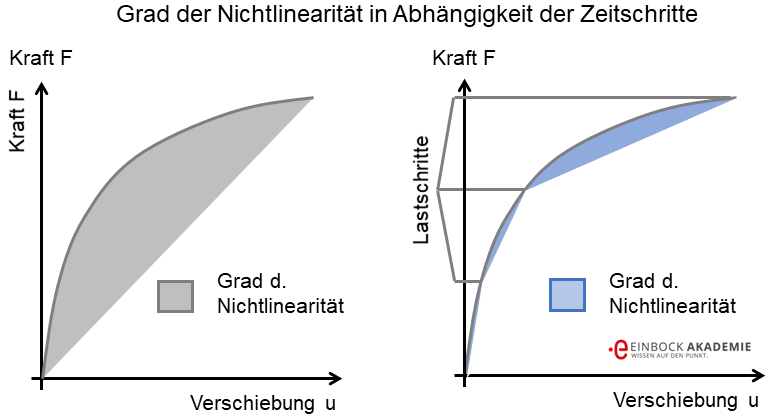
schematische Darstellung des Frades der Nichtlinearität in einer FEM Berechnung
Zu 3: Festlegung, wie die Last verkleinert wird, falls keine Konvergenz vorliegt
Sollte innerhalb eines Schrittes wider Erwarten doch keine konvergierende Lösung gefunden werden, dann muss innerhalb dieses Schrittes die Last noch einmal verfeinert werden. In obiger Abbildung sieht man ja schön, dass bei einer gleichen Einteilung der Lastschritte der Grad der Nichtlinearität je Lastschritt doch deutlich unterschiedlich ist.
Typischerweise wird hier festgelegt, dass der Lastschritt nochmals in ca. 5…10 Teillastschritte unterteilt wird, sofern kein konvergentes Ergebnis erzielt werden konnte.
4.5.2 Funktionen festlegen
Für die Festlegung der Funktionen orientieren wir uns ebenfalls an den drei im vorigen Abschnitt beschriebenen Schritten.
Zu 1: Definition einer fiktiven Zeitachse für die Lastschrittsteuerung
Um Funktionen festzulegen wird im Menü „Functions and Lists -> Define function“ gewählt (siehe linker Bild).
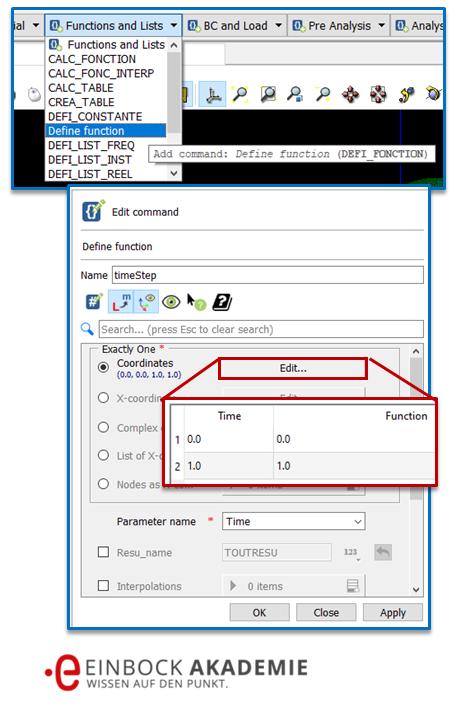
Festlegung der Zeitachse für die Lastschrittsteuerung der plastischen Berechnung in Salome Meca
Im Edit Command, dass sich daraufhin öffnet, wird die Zeitachse festgelegt (siehe ebenfalls Bild). Dies geschieht in der Art, dass
- der Name „timeStep“ eingetippt wird,
- als Parameter name „time“ im Dropdown Menü gewählt wird und
- unter Coordinates im Feld Edit die Daten der Zeitachse eingegeben werden (siehe roter Kasten).
Die Eingaben werden mit OK bestätigt. Sie besagt folgendes: die Last beginnt bei Zeitpunkt 0 und hat die Amplitude 0. Sie geht bis zu Zeitpunkt 1 und erreicht dort den Maximalwert 1.
Zu 2: Die Zeitschrittinkrementierung
Es wird im Menü „Functions and Lists -> DEFI_LIST_REEL“ gewählt (siehe Bild).
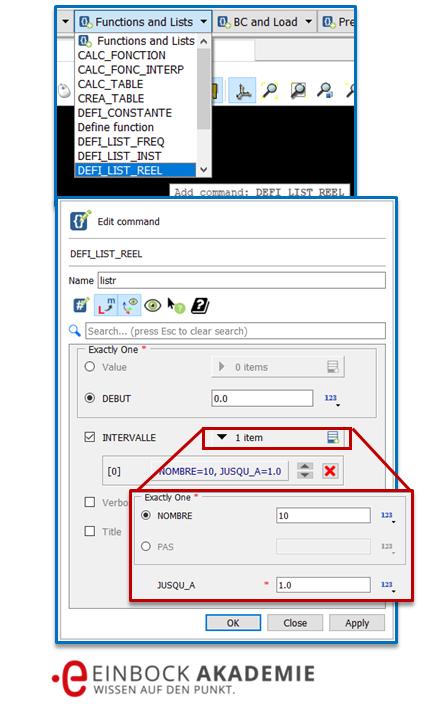
Festlegung der Zeitinkremente für die plastische Berechnung in Salome Meca
Im Edit Command, dass sich daraufhin öffnet, wird die Zeitschrittinkrementierung festgelegt (siehe Bild). Dies geschieht in der Art, dass
- der Name „lilstr“ eingetippt,
- der Punkt „DEBUT“ ausgewählt und dort 0 eingetragen
- und unter „INTERVALLE“
- bei „NOMBRE“ die Anzahl der Lastschritte (10) eingegeben und
- bei „JUSQU_A“ den Zeitpunkt, bei dem die maximale Last auftritt (1)
Die Eingaben werden mit OK bestätigt. Durch diese Eingabe habe wir jetzt festgelegt, dass die Last in 10 Teilschritten aufgebracht wird.
Zu 3: Festlegung, wie die Last verkleinert wird, falls keine Konvergenz vorliegt
Es wird im Menü „Functions and Lists -> DEFI_LIST_INST“ gewählt (siehe Bild).
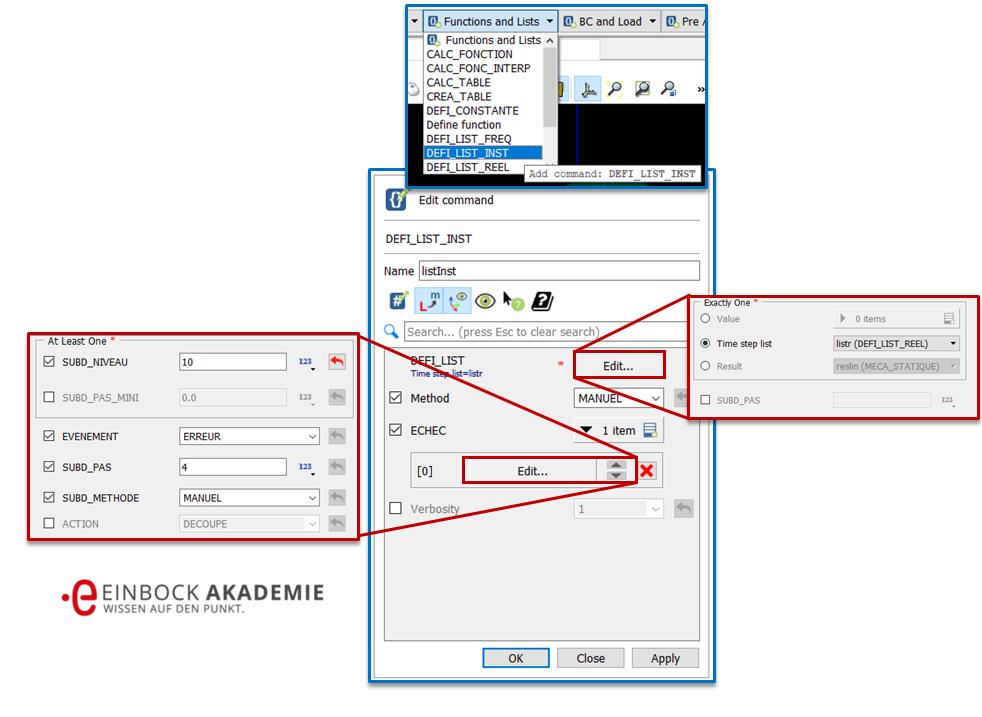
Einstellung der Substeps für eine nichtlineare FEM
Im Edit Command, dass sich daraufhin öffnet, wird die Lastverkleinerung bei Konvergenzproblemen festgelegt (siehe Bild). Dies geschieht in der Art, dass
- der Name „lilstInst“ eingetippt,
- Beim Punkt „DEFI_LIST“ Unter „Edit“ und dort bei „Time step list“ ausgewählt, dass die vorher definierte Liste mit den Lastschrittsteuerungen mit dem Namen „listr“ verwendet werden soll.
- Beim Punkt „ECHEC“ werden unter „Edit“ die folgenden Punkte gewählt:
- „SUBD_NIVEAU“ > 10
- „EVENEMENT“ > „ERREUR“: steuert die weitere Verfeinerung, wenn ein ein Fehler auftritt.
- „SUBD_PAS“ > 4: der Lastschritt wird noch einmal in vier weitere kleinere Lasten unterteilt.
- „SUBD_METHODE“ > „MANUEL“: die Vorgabe der Verkleinerung des Lastschritts erfolgt Manuell im Feld „SUBD_PAS“.
- Wählen Sie außerdem den Haken bei „Method“ -> „MANUAL“
Die Eingaben werden mit OK bestätigt. Durch diese Eingabe haben wir jetzt festgelegt, dass die Last um ein viertel verringert wird, wenn ein Fehler bei der Konvergenz auftritt.
4.5.3 Gleichungslöser einsetzen
Um auch nichtlinear rechnen zu können, muss noch ein geeigneter Gleichungslöser ausgewählt werden. Diese geschieht unter „Analysis -> STAT_NON_LINE“ (siehe Bild).
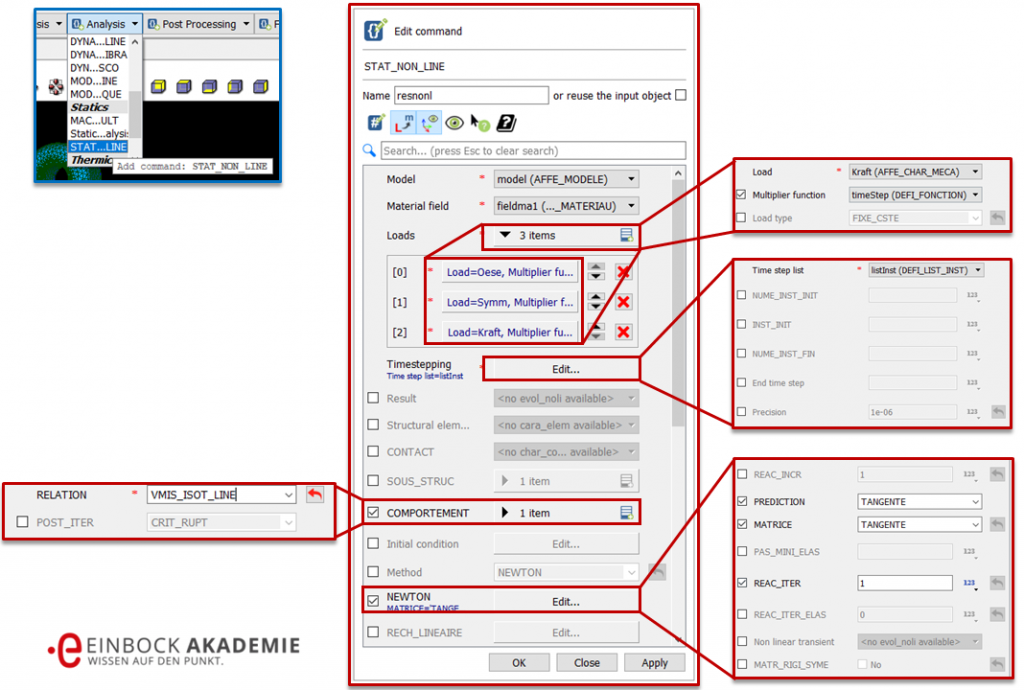
Einstellungen des Solvers in Salome Meca für eine plastische FEM Berechnung
- Im Punkt „Loads“ werden die drei Lasten / Randbedingungen ausgewählt. Das sind die
- Kraft
- Symmetriebedingung und
Zusätzlich wird jeder Last noch die Funktion zur Laststeigerung zugewiesen (
- Zusätzlich wird im Feld „Timestepping“ unter „Edit“ noch die Liste „listInst“ zur Steuerung der Zeitschritte ausgewählt.
- Anschließend setzt man bei „COMPORTEMENT“ einen Haken und wählt dort die Fließbedingung „VMIS_ISOT_LINE“. Das ist das von Mises Fließkriterium. Danach wird Fließen angenommen, wenn die von Mises Spannung die Streckgrenze erreicht (VMIS). Gleichzeitig beinhaltet dieses Kriterium die Isotrope Verfestigung (ISOT).
- Und zuletzt wird als Methode des Solvers noch das „NEWTON“-Verfahren gewählt und folgende Einstellungen unter „Edit“ getätigt:
- „PREDICTION“: „TANGENTE“
- „MATRICE“: „TANGENTE“
- „REAC_ITER“: 1.
4.5.4 Anpassung der Ergebnisse im Post Processing:
Unter „Post Processing“ können die Einstellungen angepasst werden. Dazu die rechte Maustaste auf „reslin“ drücken und dann „Edit“ wählen. Es öffnet sich das „Edit command“ aus folgender Abbildung.
- Dort wird zuerst unter „Result“ die Ergebnisse von „resnonl“ gewählt.
- Anschließend werden die folgenden auszugebenden Ergebnisse selektiert:
- „CONTRAINTE“ (SIEF_NOEU: richtungsabhängige, gemittelte Spannungen)
- „DEFORMATION“ (EPME_NOEU: Verformungen)
- „CRITERIES“ (SIEF_NOEU: richtungsabhängige, gemittelte Spannungen)
Ein wichtiges Detail ist noch zu beachten. Salome Meca bietet die Möglichkeit an, die maximale Simulationszeit festzulegen. Dadurch wird sichergestellt, dass die Berechnung nicht ewig läuft. Wird jedoch die Zeit zu knapp eingestellt, dann kann es sein, dass die Simulation ohne Ergebnis abbricht. Standardmäßig ist diese Zeit auf 15 min begrenzt! Das kann für eine plastische FEM Berechnung zu wenig sein. Um dies zu vermeiden stellen wir unter
„AsterStudy“ im Reiter „History View“ ganz links im Feld „Time“ die Zeit auf 23 h ein, siehe folgendes Bild.
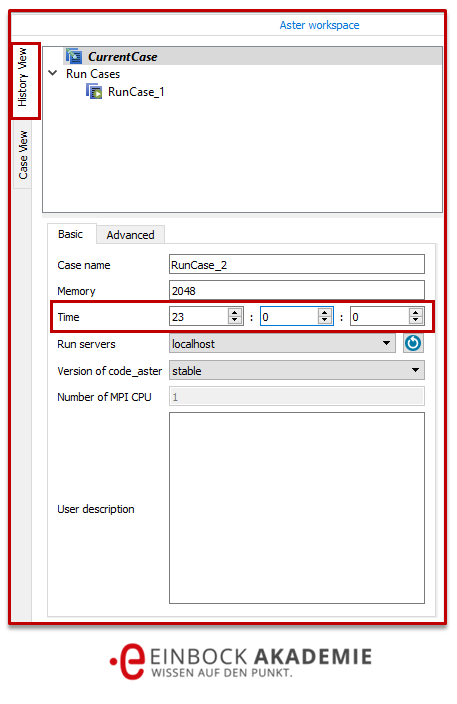
Einstellung der maximalen Rechenzeit in Salome Meca
Jetzt kann die Simulation wie im statischen Fall gestartet werden.
5 Auf den Punkt:
Eine plastische FEM Berechnung in der kostenlosen FEM Software Salome Meca ist ohne größere Probleme möglich. Etwas gewöhnungsbedürftig ist am Anfang die Einstellung der Solver Randbedingungen. Hier hilft hoffentlich die Anleitung.
Folgende Unterlagen helfen bei der Einarbeitung:
- Hintergründe und Erklärungen zur professionellen und kostenlosen FEM Software Salome Meca / CodeAster
- Eine schritt für Schritt Anleitung für eine erste linearelastische FEM Berechnung mit Salome Meca
- unsere Erklärung zur Berechnung der plastischen Stützzahl nach der FKM Richtlinie
- Die Neuber-Regel als analytische Möglichkeit zur Berechnung von Plastifizierungen
- Eine Checkliste zur Überprüfung von FEM Berechnungen und Berechnungsberichten
In jedem Fall viel Spaß mit der Software und der FEM Berechnung!
Interessieren würde mich, wie Ihnen die FEM Software Salome Meca gefällt, und ob Sie diese bereits nutzen oder planen diese zu nutzen. Ich freue mich über Ihre Kommentare, die Sie gerne über die Kommentarfunktion weiter unten hinterlassen können.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Finite Elemente Methode (FEM) Grundlagen - schnell verstehen und anwenden
Das Seminar Finite Elemente Methode (FEM) führt sie in die Grundlagen der FEM ein, erleichtert ihnen den Wiedereinstieg (z. B. nach dem Studium) oder ermöglicht Ihnen eine Vertiefung.
Sie lernen anhand der professionellen FEM Software Salome-Meca:
✓ die Grundlagen der FEM verstehen,
✓ die Überführung von CAD Modellen in FEM Modelle,
✓ FEM-Modelle genau richtig zu vernetzen,
✓ Schrauben-/Schweiß- und Klebeverbindungen zu modellieren,
✓ Baugruppen aufzubauen,
✓ Kontakte zu modellieren und
✓ FEM Ergebnisse zu interpretieren und mit der FKM-Richtlinie zu bewerten.
Die Vorteile sind:
✓ keine Vorkenntnisse erforderlich!
✓ umfangreiche Übungen.
✓ detaillierte "Klick-Anleitungen" für die FEM-Software Salome-Meca.
✓ Übertragbar auf beliebige andere Finite Elemente Software.
Weiterführende Literatur
Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses führt Sie schnell und verständlich in die Versuche und die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auslegung Ihrer Bauteile auf die Dauerfestigketi oder Betriebsfestigkeit. Sie können dann einfach Wöhlerlinien für Ihre Bauteile berechnen.
Hilfreiche Software:
Wir haben basierend auf unserer jahrelangen Erfahrung, der Mitarbeit in den Forschungsgremien zur FKM Richtlinie und dem praktischen Arbeiten mit der Richtlinie FKMmadeEASY- die Excel-Software zur FKM Richtlinie entwickelt. Wir haben dabei speziell darauf geachtet, dass diese Software
✓ einfachst möglich bedienbar
✓ gut dokumentiert und nachvollziehbar sowie
✓ optisch ansprechend ist (es soll ja auch Spaß machen).
Überzeugen Sie sich selbst davon anhand der Testversion von FKMmadeEASY - die Excel-Software zur FKM Richtlinie.
Der Autor: