Wie die Mittelspannungsempfindlichkeit bei der Berechnung der Dauerfestigkeit berücksichtigt wird
Bei der Berechnung der Wöhler Kurve, bzw. bei der experimentellen Ermittlung der Wöhlerkurven hängt die Dauerschwingfestigkeit neben dem Werkstoff auch deutlich von der Mittelspannung ab. Erfahren Sie, wie Sie die Mittelspannungsempfindlichkeit in Anlehnung an die FKM Richtlinie ermitteln und ein Dauerfestigkeitsschaubild nach Haigh interpretieren.
In diesem Artikel lernen Sie,
- Was ein Dauerfestigkeitsschaubild ist
- Wie Sie ein Dauerfestigkeitsschaubild nach Haig in Anlehnung an die FKM Richtlinie berechnen
- Wie Mittelspannungen die Wöhler-Kurve beeinflussen
- Wie die Zugfestigkeit die Mittelspannungsempfindlichkeit beeinflusst
Inhalt
- Grundbegriffe
- Einfluss der Mittelspannungen auf die Dauerfestigkeit
- Dauerfestigkeitsschaubild nach Haigh
- Berechnung der Mittelspannungsempfindlichkeit
- Der Überlastfall
- Dauerfestigkeitsschaubild experimentell ermitteln
- Zusammenfassung
- Weitere Informationen
Grundbegriffe
Die Wechselfestigkeit σzdw
Die Wechselfestigkeit eines Werkstoffes beschreibt genau die Spannungsamplitude bei der kein Dauerbruch auftritt, wenn die Spannung genau wechselnd ist. Man spricht dann auch von der Dauerfestigkeit des Werkstoffes bei rein wechselnder Zug-Druck Belastung (Spannungsverhältnis R = -1, also einer Mittelspannung von Null, σm = 0). Die Wechselfestigkeit von Metallen hängt von der Zugfestigkeit ab. Nachfolgende Tabelle gibt Anhaltswerte für die Wechselfestigkeiten von Stahl, Aluminium und Kupfer in Anlehnung an die FKM Richtlinie.
| Wechselfestigkeiten Stahl (-guss) | σzdw ~ 0,30…0,45 ∙ Rm |
| Wechselfestigkeiten Aluminium | σzdw ~ 0,30 ∙ Rm |
| Wechselfestigkeiten Kupfer | σzdw ~ 0,30…0,50 ∙ Rm |
Das Spannungsverhältnis R
Das Spannungsverhältnis R ist eine Kennzahl zur Beschreibung von Schwingspielen. Es berechnet sich aus dem Verhältnis aus Unterspannung σu zu Oberspannung σo: R = σu / σo = (σm - σa)/(σm + σa).
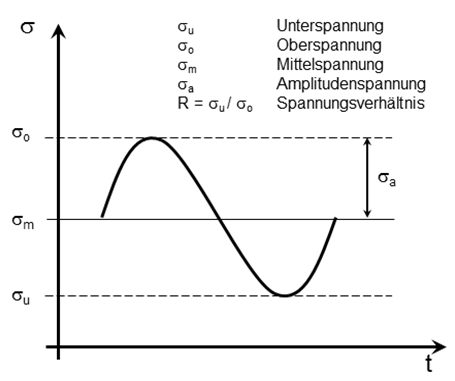
Schematische Darstellung eines Schwingspieles inkl. Erklärung des Spannungsverhältnis R
- Rein wechselnde Lasten mit einer Mittelspannung σm = 0 MPa haben ein
Spannungsverhältnis R = -1. - Rein schwellende Lasten mit einer Unterspannung σu = 0 MPa haben ein
Spannungsverhältnis R = 0.
Prinzipieller Einfluss der Mittelspannungen auf die Dauerfestigkeit
Neben einer rein wechselnder Zug-Druck Belastung (Spannungsverhältnis R = -1, also einer Mittelspannung von Null, σm = 0) existieren noch beliebig viele Lastfälle mit anderen Mittelspannungen oder Spannungsverhältnissen. Diese Lastfälle haben dann eine von der Zug-Druck-Wechselfestigkeit σzdw verschiedene Dauerfestigkeit σAD.
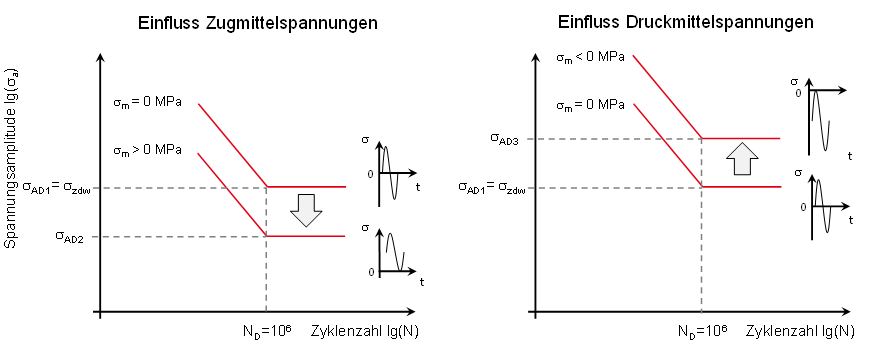
Einfluss der Mittelspannungen auf die Wöhlerkurve
Mittelspannungen im Zugbereich (σm > 0 MPa) führen generell zu einer geringeren dauerfest ertragbaren Amplitude σAD, wohingegen Druckmittelspannungen (σm < 0 MPa) die dauerfest ertragbare Amplitude σAD erhöhen (siehe obere Abbildung). Kurz gesagt gilt:
- Zugmittelspannungen senken die Dauerfestigkeit und
- Druckmittelspannungen erhöhen die Dauerfestigkeit.
- Den Zusammenhang zwischen der Mittelspannung und der dauerfest ertragbaren Amplitude liefert der Mittelspannungseinfluss fM. Wie stark der Werkstoff auf Mittelspannungen reagiert wird über die Mittelspannungsempfindlichkeit M beschrieben.
Eine grafische Darstellung des Mittelspannungseinfluss erfolgt üblicherweise in dem Dauerfestigkeitsschaubild nach Haigh oder Smith.
Das Dauerfestigkeitsschaubild nach Haigh analog der FKM Richtlinie
Im Dauerfestigkeitsschaubild nach Haigh wird die dauerfest ertragbare Amplitude in Abhängigkeit der Mittelspannung dargestellt. Mittelspannungen können als statische Beanspruchungen gesehen werden. Deren Beanspruchbarkeit z. B. die Zugfestigkeit ist. Amplitudenspannungen sind schwingende Spannungen, deren Beanspruchbarkeit die Wechselfestigkeit ist.
Die Beanspruchbarkeit einer beliebigen Überlagerung von Mittelspannung und Amplitudenspannung gibt das Dauerfestigkeitsschaubild an. Dazu werden die dauerfest ertragbare Amplitude auf der Ordinate („y-Achse“) und die Mittelspannung auf der Abszisse („x-Achse“) aufgetragen. Es lässt sich damit sehr anschaulich für eine beliebige Mittelspannung σm die dauerfest ertragbare Spannungsamplitude σAD ermitteln siehe folgende Abbildung.
Alle Punkte, die auf einer Ursprungsgerade liegen, haben dasselbe Spannungsverhältnis R. Die Punkte auf der Ordinate entsprechen alle einer rein wechselnden Beanspruchung (R = -1). Analog zur Abbildung über den Einfluss der Mittelspannung auf die Wöhlerkurve sinkt die dauerfest ertragbare Spannungsamplitude für Zugmittelspannungen und sie steigt für Druckmittelspannungen (siehe folgendes Bild).
Das Dauerfestigkeitsschaubild nach der FKM Richtlinie lässt sich einfach durch Geradenstücke konstruieren und damit einfach mathematisch beschreiben (siehe untere Abbildung).
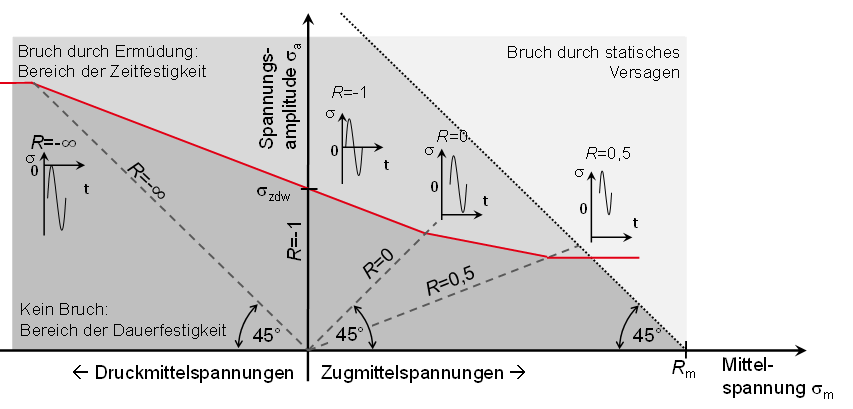
Mittelspannungseinfluss am Beispiel des Dauerfestigkeitsschaubildes nach der FKM Richtlinie
Das Dauerfestigkeitsschaubild stellt eine Grenzkurve dar. Wertepaare von wirkenden Spannungen (σm|σa) die genau auf dieser Grenzkurve liegen, sind dauerfest ertragbar. Es tritt kein Dauerbruch auf.
Liegen diese unterhalb der Grenzkurve sind diese mit einem Sicherheitsfaktor dauerfest ertragbar. Alle Wertepaare oberhalb der Grenzkurve sind nicht mehr dauerfest ertragbar, werden also durch Schwingbruch oder statisch versagen (siehe obige Abbildung Mittelspannungseinfluss am Beispiel des Dauerfestigkeitsschaubildes nach der FKM Richtlinie).
Die Konstruktion des Dauerfestigkeitsschaubildes nach Haigh erfolgt mit Hilfe von vier Geradenstücken, der Mittelspannungsempfindlichkeit Mσ und der Zug-Druck Wechselfestigkeit des Werkstoffes σzdw. Die Mittelspannungsempfindlichkeit ist die Steigung der Geraden durch die Zug-Druck Wechselfestigkeit für Spanungsverhältnisse von -∝ < R ≤ 0 (vgl. Abbildung Dauerfestigkeitsschaubild für Normalspannungen unten).
Für Spannungsverhältnisse 0 < R ≤ 0,5 wird als Mittelspannungsempfindlichkeit M'σ verwendet. Für R > 0,5 und R > 1 verläuft das Dauerfestigkeitsschaubild horizontal. Auf der y-Achse läuft das Dauerfestigkeitsschaubild durch die Zug-Druck-Wechselfestigkeit des Werkstoffes. Auf der x-Achsedurch die statische Festigkeit, symbolisiert durch die Zugfestigkeit.
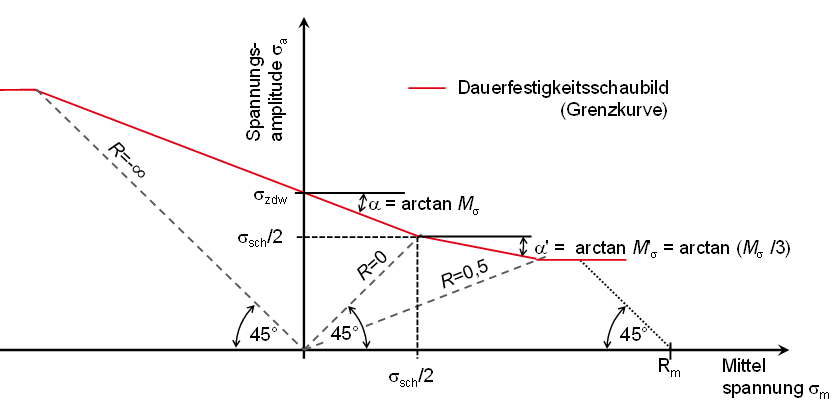
Dauerfestigkeitsschaubild Haigh für Normalspannungen nach FKM Richtlinie
Die Berechnung der Mittelspannungsempfindlichkeit
Für die Berechnung der Mittelspannungsempfindlichkeiten Mσ und M'σ liefert die FKM-Richtlinie Näherungsgleichungen:
Mσ = am⋅ 10-3 ⋅ Rm /MPa + bm
M'σ =1/3 Mσ
Die zugehörigen Kennwerte fasst nachstehende Tabelle abhängig von der Werkstoffgruppe zusammen. Je spröder und je höherfest der Werkstoff ist, umso steiler ist das Dauerfestigkeitsschaubild. Der Werkstoff reagiert also umso kritischer auf Mittelspannungen je spröder er ist (eine steigende Festigkeit führt gleichzeitig zur Abnahme der Zähigkeit und damit einer höheren Mittelspannungsempfindlichkeit).
Tabelle: Kennwerte zur Berechnung der Mittelspannungsempfindlichkeit
| Stahl | Stahlguss GS | Gusseisen | Aluminium-knetlegierung | Aluminium-gusslegierung | |||
| mit Kugel-graphit GJS | Temperguss GJM | mit Lamellen-graphit GJL | |||||
| am | 0,35 | 0,35 | 0,35 | 0,35 | 0 | 1,0 | 1,5 |
| bm | -0,1 | 0,05 | 0,08 | 0,13 | 0,5 | -0,04 | 0,2 |
Die Berücksichtigung des Überlastfall nach der FKM Richtlinie
Bei einem Festigkeitsnachweis wird ein Beanspruchungszustand bestehend aus Mittelspannun σm und Amplitudenspannung σa mit dem Dauerfestigkeitsschaubild verglichen (Abbildung Visualisierung des Mittelspannungseinflusses). Gesucht ist die dauerfest ertragbare Amplitude. Das Problem dabei ist, dass ein Punkt (Beanspruchungszustand) mit einer Kurve (Dauerfestigkeitsschaubild) verglichen werden muss. Damit dies möglich ist, wird eine zusätzliche Information benötigt. Diese liefert der Überlastfall.
Der Überlastfall beschreibt in welchem Verhältnis sich Mittel- und Amplitudenspannung bei einer Laständerung verhalten. In Summe gibt es nach der FKM-Richtlinie folgende Überlastfälle:
- Überlastfall F1: Konstante Mittelspannung (σm = konst.)
- Überlastfall F2: Konstantes Spannungsverhältnis (R = konst.)
- Überlastfall F3: Konstante Unterspannung (σu = konst.)
- Überlastfall F4: Konstante Oberspannung (σ0 = konst.)
Der häufigste Fall ist der sogenannte Überlastfall F2. Er bedeutet eine proportionale Änderung von Mittel- und Amplitudenspannung, also ein konstantes Spannungsverhältnis R.
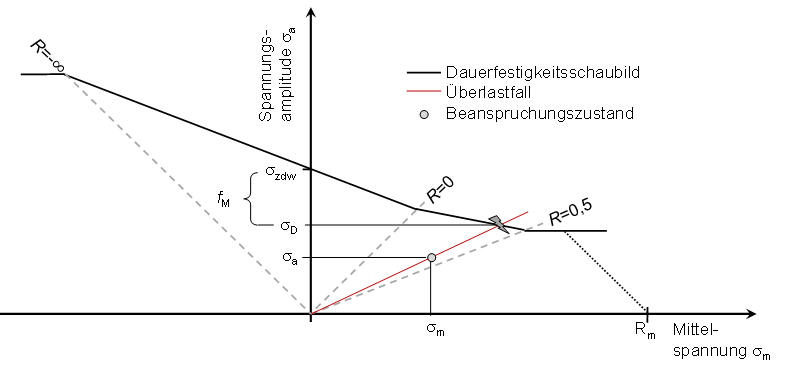
Visualisierung des Mittelspannungseinflusses
Für den Überlastfall F2 befinden sich alle möglichen Beanspruchungszustände auf der in oberen Abbildung dargestellten Ursprungsgerade durch den zu bewertenden Beanspruchungszustand. Der Schnittpunkt dieser Gerade mit dem Dauerfestigkeitsschaubild ergibt den gerade noch dauerfest ertragbaren Beanspruchungszustand. Dessen Spannungsamplitude ist die gesuchte Dauerfestigkeit σD. Das Verhältnis der Zug-Druck Wechselfestigkeit σzdw zu dieser Dauerfestigkeit σD ist der Mittelspannungseinfluss fM.
fM = σD / σzdw.
Die untere Abbildung zeigt alle Überlastfälle nach der FKM Richtlinie.
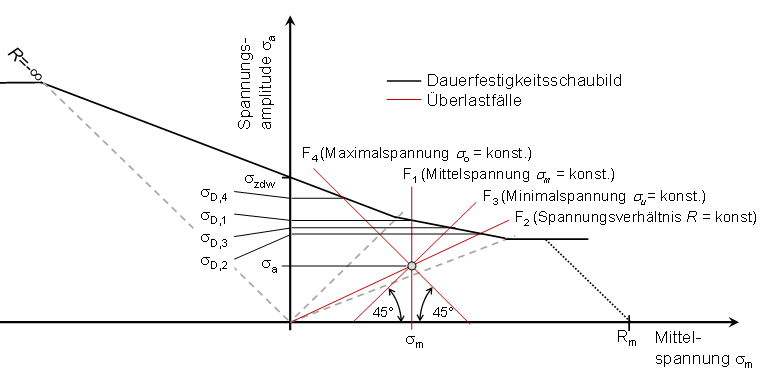
Überlastfälle nach der FKM Richtlinie
Jetzt wird deutlich, dass die rechnerische Beschreibung der Dauerfestigkeit
- vom Überlastfall,
- der Mittelspannungsempfindlichkeit Mσ und damit dem Werkstoff sowie der Zugfestigkeit, als auch davon abhängt,
- in welchem Bereich des Dauerfestigkeitsschaubildes ausgewertet wird.
Für den Überlastfall F2 berechnet sich der Mittelspannungseinfluss fM wie folgt:
- Für R >1: fM = 1/(1 - Mσ)
- Für - ∝ ≤ R ≤ 0: fM = 1/(1 + Mσ ⋅ σm/σa)
- Für 0 < R < 0,5: fM = (3 + Mσ)/((1 + Mσ)⋅(3 + Mσ ⋅ σm/σa))
- Für R ≥ 0,5: fM = (3 + Mσ)/(3⋅(1 + Mσ)²)
Für die restlichen Überlastfälle wird auf die FKM Richtlinie verwiesen.
Die experimentelle Ermittlung des Dauerfestigkeitsschaubilds nach Haigh und der Mittelspannungsempfindlichkeit
Um für eigene Werkstoffe den Mittelspannungseinfluss experimentell zu ermitteln werden mindestens zwei Versuche benötigt. Ein Versuch zur Ermittlung der Zug-Druck-Wechselfestigkeit σzdw (bei R = -1) und ein Versuch mit rein schwellender Beanspruchung zur Ermittlung der Dauerfestigkeit σD bei R = 0. Beide Versuche werden in das Dauerfestigkeitsdiagramm eingezeichnet und daraus die Mittelspannungsempfindlichkeit Mσ berechnet:
fM = σD / σzdw = 1/(1 + Mσ ⋅ σm/σa)
wobei für den Schwellenden Fall mit R = 0 gilt: σm/σa = 1, da σm = σa. Damit vereinfacht sich obige Gleichung wie folgt:
fM = σD / σzdw = 1/(1 + Mσ)
Umformen liefert:
Mσ = σzdw / σD - 1.
Die Mittelspannungsempfindlichkeit M'σ für 0 < R < 0,5 berechnet sich nach folgender Gleichung:
M'σ = 1/3 Mσ.
Auf den Punkt
- Die Wechselfestigkeit eines Werkstoffes beschreibt genau die Spannungsamplitude bei der kein Dauerbruch auftritt.
- Die Wechselfestigkeit von Metallen hängt von der Zugfestigkeit ab
- Das Spannungsverhältnis R ist eine Kennzahl zur Beschreibung von Schwingspielen. Es berechnet sich aus dem Verhältnis aus Unterspannung σu zu Oberspannung σo.
- Zug-Mittelspannungen führen zu einem Absenken der Dauerfestigkeit, sind also tendenziell kritisch.
- Druck-Mittelspannungen führen zu einem Ansteigen der Dauerfestigkeit, sind also tendenziell positiv.
- Die Mittelspannungsempfindlichkeit beschreibt den Einfluss der Mittelspannungen auf die Dauerfestigkeit in Abhängigkeit der Zugfestigkeit und des Werkstoffes.
- Spröde oder hochfeste Werkstoffe reagieren kritischer auf Mittelspannungen als duktile Werkstoffe.
- Im Dauerfestigkeitsschaubild nach Haigh wird die dauerfest ertragbare Amplitude in Abhängigkeit der Mittelspannung dargestellt. Es lässt sich in Anlehnung an die FKM Richtlinie durch vier Geradenstücke beschreiben.
- Die Steigung der Geradenstücke beschreibt die Mittelspannungsempfindlichkeit Mσ.
- Eine experimentelle Ermittlung des Dauerfestigkeitsschaubildes ist effizient durch nur zwei Versuche bei R = -1 und R = 0 möglich.
Weiterführende Informationen zur FKM Richtlinie und Wöhlerkurven
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminare zur FKM Richtlinie:
Haben Sie Interesse an einer schnellen Anwendung und einem einfachen Einstieg in die komplexe FKM Richtlinie? Dann ist evtl. unsere Schulung zur FKM Richtlinie für Sie richtig.
Diese ist genau richtig für Sie, wenn Sie
- die FKM Richtlinie schnell anwenden möchten.
- Ihre FEM Ergebnisse bewerten wollen.
- die Hintergründe der FKM Richtlinie verstehen und üben wollen.
Weiterführende Literatur
Um Wöhlerkurven zu berechnen und ein tieferen Einblick in die Betriebsfestigkeit und die Bewertung von FEM Ergebnissen zu bekommen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses fürht Sie schnell und verständlich in die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Berechnung der Lebensdauer.

Gibt es zu der Tabelle: Kennwerte zur Berechnung der Mittelspannungsempfindlichkeit
auch Kennwerte für die Zink Druckgusslegierungen?
Hallo Johannes,
vielen Dank für dein Interesse an den Themen der Betriebsfestigkeit.
Leider kennen ich die Kennwerte für die Mittelspannungsempfindlichkeit von Zink Druckgusslegierungen nicht. Evtl. finden sich in einschlägigen Forschungsgremien oder bei Lieferanten / Giessern hier diese Kennwerte.
In den typischen Quellen konnte ich leider keine Informationen finden.
Ich hoffe, dass Sie hier eher fündig werden.
Ihnen schöne Grüße und viel Erfolg
Stefan Einbock
Guten Tag Herr Stefan Einbock,
ich möchte Ihnen für Ihre inhaltsstarke und praxisrelevante Artikel danken.
Danke und viele Grüße
Alexander Brunner
In der Formel zum Spannungsverhältnis hat sich ein Fehler eingeschlichen.
Es müsste heissen: R= (σm − σa) / (σm + σa)
Hallo Hr. Surber,
vielen Dank für den wertvollen Hinweis!
Ich habe den Fehler behoben.
Grüße und viel Spass beim Rechnen
Stefan Einbock