Ein Festigkeitsnachweis nach der FKM Richtlinie ist aufwändig, insbesondere der Nachweis der Schwingfestigkeit. Leider gibt es für den Nennspannungsnachweis nur wenig Softwareunterstützung. Deshalb haben wir für Sie einerseits ein paar Tipps zusammengestellt, die den Schwingfestigkeitsnachweis nach der FKM-Richtlinie beschleunigen.
Dieser Artikel ist der zweite Teil einer Artikelserie. Im ersten Artikel haben wir den effizienten statischen Nachweis nach der FKM-Richtlinie betrachtet. Hier liegt der Fokus auf dem Schwingfestigkeitsnachweis.
Und zusätzlich haben wir die Software zur FKM Richtlinie FKMmadeEASY um den Nennspannungsnachweis ergänzt. Damit können Sie jetzt einen Festigkeitsnachweise nach der gesamten FKM Richtlinie in der 6. Auflage bequem und schnell mit unserer Software durchführen.
In diesem Artikel lernen Sie,
- Welche Einflüsse die Schwingfestigkeit nach der FKM-Richtlinie* beschreiben
- Wie Sie bei dem Festigkeitsnachweis Zeit sparen können, indem Sie nur die wichtigen Faktoren berechnen.
Inhalt
1. Grundidee
Die Anzahl der Einflüsse auf die Schwingfestigkeit ist hoch. Deshalb betrachten wir beide Nachweise separat. Den effizienten statischen Nachweis nach der FKM-Richtlinie im ersten Teil dieser Artikelserie und den Schwingfestigkeitsnachweis in diesem Artikel. Zusätzlich werden die einzelnen Einflüsse nach Ihrer Wirkung aufgeteilt. Denn es gibt
- Festigkeitsmindernde (z. B. Temperatur) und
- Festigkeitssteigernde Einflüsse (z. B. Stützwirkung).
Diese Einteilung hat einen wesentlichen Vorteil in Bezug auf die Effizienz bei einem Festigkeitsnachweis:
- Festigkeitsmindernde Einflüsse müssen bei einem Nachweis berücksichtigt werden, wohingegen
- Festigkeitssteigernde Einflüsse im ersten Schritt vernachlässigt werden können.
Welchen Vorteil bietet jetzt dieses Vorgehen?
Wenn der Nachweis nach dieser Vorgehensweise erfolgreich ist, dann hat man sich die (teilweise aufwändige) Berechnung der festigkeitssteigernden Einflüsse gespart. Der Nachweis liegt somit auf der sicheren Seite, und war relativ effizient.
Ist der Nachweis nach der Vorgehensweise nicht erfolgreich, dann kann man schrittweise die festigkeitssteigernden Einflüsse in den Nachweis mit aufnehmen.
2. Einflüsse auf die Schwingfestigkeit
Der Nachweis der Schwingfestigkeit erfolgt prinzipiell in drei Schritten (die FKM-Richtlinie geht hier 6 Schritte).
- Zuerst wird die Beanspruchung in Form eines Lastkollektives ermittelt. Diese gibt an, welche Lasten das Bauteil sieht.
- Demgegenüber steht die Beanspruchbarkeit des Bauteils als Bauteilwöhlerlinie. Damit sagt sie aus, welche Lasten das Bauteil erträgt.
- Der Vergleich von Beanspruchung und Beanspruchbarkeit geschieht in Schritt drei, der Schadensakkumulation. Bei der Schadensakkumulation (oder auch Miner-Regel) wird die Beanspruchung (meist in Form eines Lastkollektives) der Beanspruchbarkeit (also der Bauteilwählerlinie) gegenübergestellt. Es wird dann eine Lebensdauer berechnet.
Bei einem Festigkeitsnachweis müssen alle drei Schritte durchlaufen werden. Potenziale zur schnelleren Bearbeitung bei einem Nachweis nach der FKM-Richtlinie ergeben sich in den Schritten 2 und 3. Konkret bedeutet dies die Potenziale entfalten sich bei der Berechnung der:
- Wöhlerlinie nach den Kapiteln 2.3 bzw. 4.3, Konstruktionskennwerte und Kapitel 2.3 bzw. 4.4).
- Schadensakkumulation nach Miner in den Kapiteln 2.4 und 4.4.
Jeder der Einflüsse wird wieder nach festigkeitssteigernd und festigkeitsmindernd berücksichtigt.
3. Berechnung der Bauteil-Wöhlerlinie nach der FKM Richtlinie
Die Bauteilwöhlerlinie wird in der FKM Richtlinie in Kapitel 4.4 (bei Berechnung mit FEM Spannungen) und Kapitel 2.4 (bei Berechnung mit Nennspannungen) ermittelt. Sie wird durch die drei Parameter
- Amplitude der Bauteil-Dauerfestigkeit σAK (Gleichung 2.4.4 bzw. 4.4.4)
- Knickpunktzyklenzahl ND, ND,II (Tabelle 2.4.3 bzw. 4.4.3) und
- Neigungsexponent k, kII (Tabelle 2.4.3 bzw. 4.4.3).
Möglichkeiten für einen effizienteren Nachweis ergeben sich hier nur bei der Berechnung der Bauteildauerfestigkeit. Die Knickpunktzyklenzahl ND und der Neigungsexponent k müssen berücksichtigt werden.
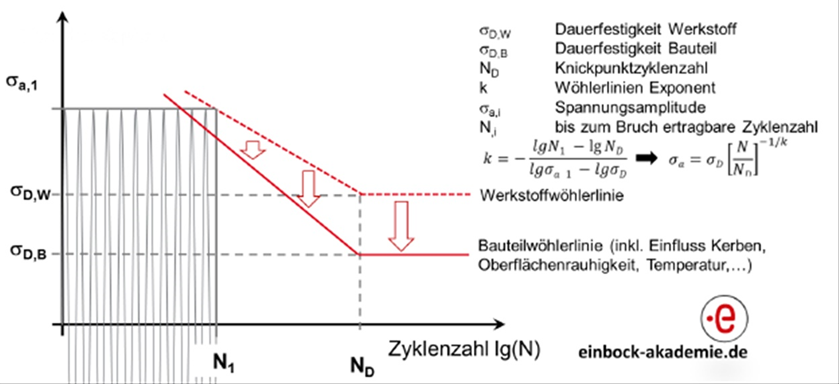
Berechnung der Bauteilwöhlerlinie nach der FKM-Richtlinie
3.1. Berechnung der Bauteil-Dauerfestigkeit
Alle wesentlichen Einflüsse des Bauteils auf die Wöhlerlinie fließen in die Berechnung der Bauteil-Dauerfestigkeit ein. Nach der FKM Richtlinie wird die Bauteildauerfestigkeit wie folgt berechnet:
σAK = σWK · KAK Bauteil-Dauerfestigkeit (Gleichung 2.4.4. bzw. 4.4.4),
mit dem Mittelspannungsfaktor KAK und der Bauteil-Wechselfestigkeit σWK
σWK = σW,zd / KWK Bauteil-Wechselfestigkeit (Gleichung 2.4.1 bzw. 4.4.1),
es ist KWK der Konstruktionsfaktor und σW,zd die Werkstoff-Wechselfestigkeit.
Der Konstruktionsfaktor KWK wird wie folgt berechnet:
KWK = 1/(ns · KV · KS · KNL,E) · [1+1/Kf · (1/KR - 1)].
Mit den Einflüssen:
- Kf, Schätzwert für die Kerbwirkungszahl. Berücksichtigt die Abhängigkeit des Rauheitsfaktors von der Kerbschärfe (je schärfer die Kerbe, umso geringer ist der Einfluss der Rauheit).
- nσ, die Stützzahl berücksichtigt den Einfluss von Kerben und der Spannungsverteilung
- KR, der Rauheitsfaktor berücksichtigt den Einfluss der Oberflächenrauheit
- KV, der Randschichtfaktor berücksichtigt den Einfluss einer Randschicht
- KS, der Schutzschichtfaktor berücksichtigt den Einfluss einer Schutzschicht auf die Ermüdungsfestigkeit eines Bauteiles aus Aluminiumwerkstoff
- KNL,E Berücksichtigung des nichtlinear-elastischen Spannungs-Dehnungs-Verhaltens von GJL bei Biegung
Damit berechnet sich die Bauteil-Dauerfestigkeit in Abhängigkeit der Werkstoffwechselfestigkeit und der Bauteileinflüsse zu
σAK = σWK · KAK = σW,zd / KWK * KAK = σW,zd / {1/(nσ · KV · KS · KNL,E) · [1+1/Kf · (1/KR - 1)]} · KAK
σAK = σW,zd · nσ · KV · KS · KNL,E · 1 / [1+1/Kf · (1/KR - 1)] · KAK
3.1.1 Die festigkeitssteigernden Einflüsse sind
- Kf, Schätzwert für die Kerbwirkungszahl. Berücksichtigt die Abhängigkeit des Rauheitsfaktors von der Kerbschärfe (je schärfer die Kerbe, umso geringer ist der Einfluss der Rauheit).
- nσ, die Stützzahl berücksichtigt den Einfluss von Kerben und der Spannungsverteilung
- KV, der Randschichtfaktor berücksichtigt den Einfluss einer Randschicht
3.1.2 Die festigkeitsmindernden Einflüsse sind
- KR, Rauheitsfaktor berücksichtigt den Einfluss der Oberflächenrauheit
- KS, der Schutzschichtfaktor berücksichtigt den Einfluss einer Schutzschicht auf die Ermüdungsfestigkeit eines Bauteiles aus Aluminiumwerkstoff
- KNL,E, Berücksichtigung des nichtlinear-elastischen Spannungs-Dehnungs-Verhaltens von GJL bei Biegung
3.2 Tipps für einen effizienteren Nachweis:
Wie beim statischen Nachweis (siehe auch den Artikel zum effizienten statischen Nachweis nach der FKM-Richtlinie) schauen wir uns die beiden festigkeitssteigernden Einflüsse detaillierter an:
3.2.1 Der Schätzwert für die Kerbwirkungszahl Kf:
Dieser Kennwert berücksichtigt die Abhängigkeit des Rauheitsfaktors KR von der Kerbschärfe. Es wird angenommen, dass sich Oberflächenrauheiten weniger kritisch auswirken, je schärfer die Kerbe ist. Die Kerbschärfe wird dabei über den Schätzwert für die Kerbwirkungszahl Kf berücksichtigt.
Eine konservative und schnelle Annahme ist, dass das Bauteil ungekerbt ist (Kf = 1). In diesem Fall wird der Einfluss der Oberflächenrauheit maximal berücksichtigt. Man spart sich die Berechnung der Kerbwirkungszahl Kf.
3.2.2 Die Stützzahl nσ
Mit der Berechnung der Stützzahl wird dem Effekt Rechnung getragen, dass eine ungleiche Spannungsverteilung zu einer Stützwirkung führt und die Festigkeit anhebt. Kerben wirken sich dadurch bei schwingender Belastung nicht so kritisch aus, wie bei statischer Berechnung angenommen.
Es gibt mehrere Möglichkeiten hier Zeit zu sparen:
- Vernachlässigung der Stützzahl
- Auswahl des geeigneten Stützzahlkonzepts
- Einfache Berechnung des bezogenen Spannungsgefälles
Zu 1) Vernachlässigung der Stützzahl:
Eine konservative und schnelle Annahme ist, dass die Stützzahl nicht wirksam ist (nσ = 1). Man spart sich dadurch die z.T. aufwändige Berechnung der Stützzahl.
Eine Ausnahme bildet hier die Werkstoffmechanische Stützzahl, denn diese kann wegen des statistischen Größeneinflusses tatsächlich auch Werte kleiner 1 annehmen kann.
Zu 2) Auswahl des geeigneten Stützzahlkonzepts
Soll die Stützzahl doch berücksichtigt werden, steht man vor der Wahl, welches Stützzahlkonzept gewählt werden soll. Hier bietet die Richtlinie nämlich zwei verschiedene Konzepte an:
- Das Stützzahlkonzept nach Stieler und
- Die werkstoffmechanische Stützzahl.
Die wesentlichen Unterschiede zwischen den beiden Konzepten zeigt die folgende Abbildung.
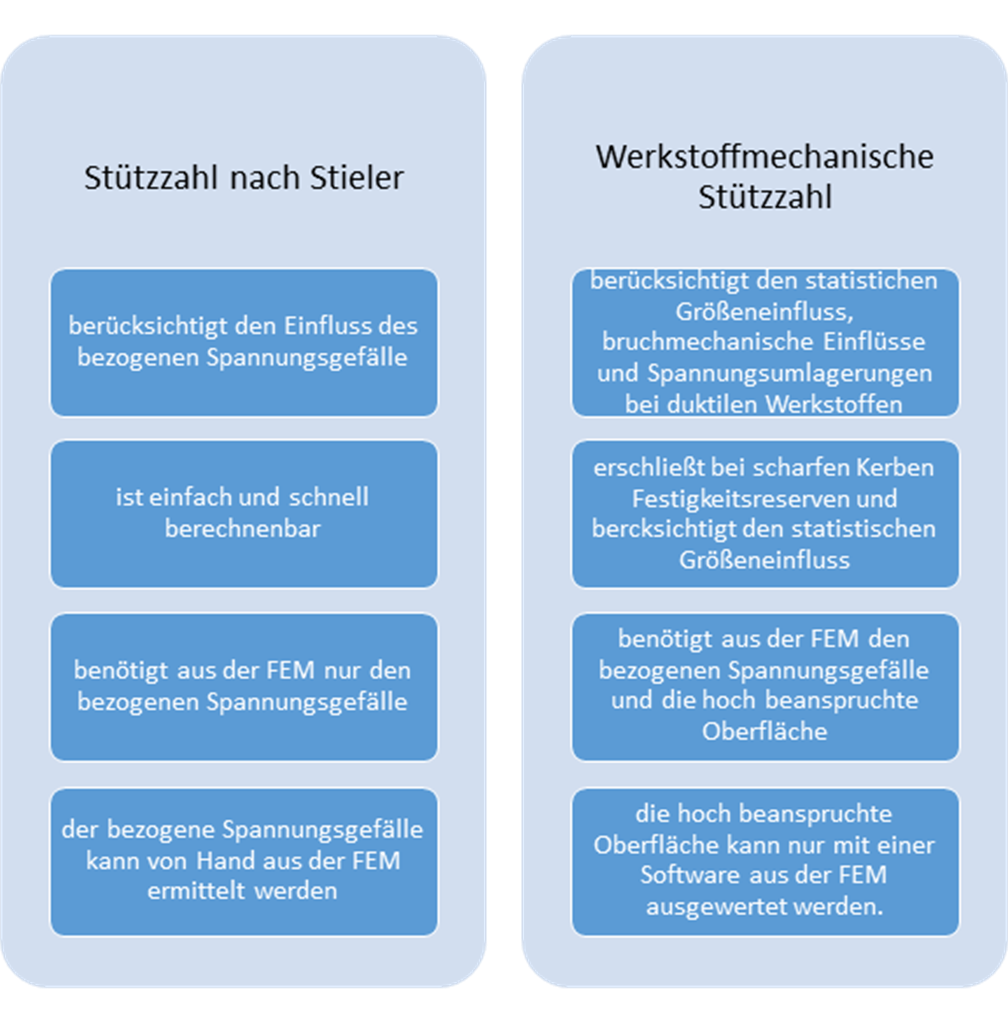
Vergleich der Stützzahlkonzepte nach Stieler und werkstoffmechanisch nach der FKM-Richtline
In wahrscheinlich 99 % der Fälle ist das einfachere Verfahren nach Stieler völlig ausreichend. Warum? Weil hiermit bereits hohe Potenziale der Stützwirkung gehoben werden. Gleichzeitig wird der Statistische Größeneinfluss in den meisten Maschinenbau und Fahrzeugbau Anwendungen keine dominante Rolle spielen.
Den statistischen Größeneinfluss kann man am besten mit dem Beispiel einer Kette erklären. Die Bruchwahrscheinlichkeit einer Kette wird bei gleicher Belastung ansteigen, je mehr Kettenglieder sie hat. Denn mit steigender Anzahl an Kettengliedern steigt die Wahrscheinlichkeit, dass eines dieser Kettenglieder brechen wird. Gleiches gilt für Bauteile. Je mehr Bereiche in einem Bauteil hoch beansprucht sind, umso wahrscheinlicher ist es, dass in einem dieser Bereiche ein kritischer Riss entstehen kann.
In den meisten Bauteilen werden allerdings Kerben zum Ausfall führen. Dann sind die hochbeanspruchten Bereiche vergleichsweise gering und der statistische Größeneinfluss vernachlässigbar. Eine Berücksichtigung der Stützzahl nach dem Konzept von Stieler ist ausreichend.
Eine konservative und effiziente Wahl des Stützzahlkonzeptes ist
- Das Stützzahlkonzept nach Stieler in wahrscheinlich 99% der Fälle
Wann sollte dann die werkstoffmechanische Stützzahl angewandt werden? Erst,
- wenn scharfe Kerben vorliegen und der Nachweis nach dem Stützzahlkonzept von Stieler nicht erfolgreich war. Oder
- wenn tatsächlich mit einem Einfluss der Bauteilgröße (und damit dem statistischen Größeneinfluss) gerechnet werden muss. Aber Achtung: die Berechnung der hoch beanspruchten Oberfläche aus der FEM ist nur mit einer geeigneten Software möglich. Eine händische Auswertung wie beim bezogenen Spannungsgefälle ist leider unmöglich.
Zu 3) Einfache Berechnung des bezogenen Spannungsgefälles
Für beide Konzepte zur Berechnung der plastischen Stüzzahl wird das bezogene Spannungsgefälle Gσ benötigt. Wenn FEM Ergebnisse bewertet werden sollen, dann muss dieses aus der FEM ausgewertet werden.
Leider wird für die exakte Berechnung des bezogenen Spannungsgefälles ein sehr feines FEM Netz benötigt (ca.25 Elemente über dem Radius). Siehe dazu unseren Artikel zur Auswahl der richtigen Netzfeinheit für die Berechnung von Spannungsgefälle. Das ist ein deutlich feineres Netz als es für die genaue Berechnung der maximalen Spannungen notwendig ist (ca. 5 Elemente über dem Radius), vgl. auch unseren Artikel zur Netzfeinheit von FEM Netzen.
Die Ursache liegt darin, dass die FEM ist eine Näherungslösung ist und der bezogene Spannungsgefälle eine Größe ist, die von der Spannung abgeleitet wurde. Dadurch muss die Netzfeinheit für die Berechnung des bezogenen Spannungsgefälles höher sein als für die Berechnung der maximalen Spannung.
ABER: jetzt zu unserem Tipp. Üblicherweise ist das bezogene Spannungsgefälle bei zu grober Vernetzung flacher, als für die exakte, feine Vernetzung. Ein flacheres bezogenes Spannungsgefälle führt jedoch zu einer kleineren Stützwirkung. Damit liegt das Ergebnis auf der sicheren Seite.
Für eine konservative und schnelle Abschätzung des Spannungsgefälle Gσ ist
- meist das normale FEM Netz von ca. 5 Elementen über dem Radius ausreichend. Gleichzeitig ist
- es konservativer, wenn über mehrere Elemente hinweg ausgewertet wird und dadurch die Auswertetiefe steigt.
Erst wenn dieser Nachweis nicht ausreichend ist, ist es ratsam, den Mehraufwand der feineren Vernetzung in Kauf zu nehmen, um den bezogenen Spannungsgefälle genau zu berechnen. Sind die Kerben sehr scharf oder muss der statistische Größeneinfluss berücksichtigt werden, sollte mit der werkstoffmechanischen Stützzahl gerechnet werden.
4. Berechnung der Lebensdauer mittels Schadensakkumulation
Bei der Schadensakkumulation werden die Beanspruchungen in Form des Lastkollektives der Beanspruchbarkeit (der Wöhlerlinie) gegenübergestellt. Detailliertere Infos dazu auch in unserem Artikel zur Schadensakkumulation nach der Miner-Regel oder auch ein Beispiel zur Lebensdauerberechnung nach der Miner-Regel.
Bei der Schadensakkumulation nach Palmgren-Miner oder kurz: Miner-Regel existieren verschiedene Modifikationen. In der FKM-Richtlinie werden zwei Konzepte zur Auswahl gestellt:
- Miner elementar und
- Miner konsequent.
Eine Übersicht über die Unterschiede zeigt die folgende Abbildung.
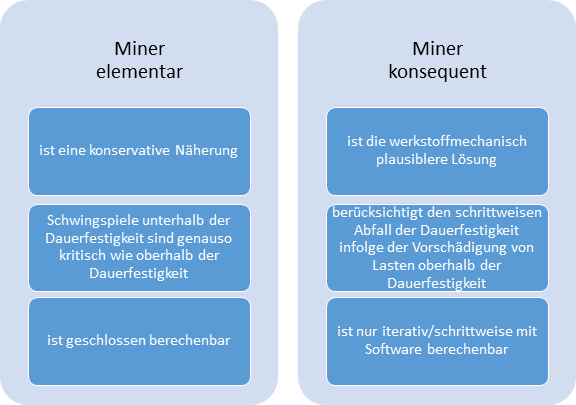
Vergleich von Miner-elementar und Miner-konsequent als Schadensakkumulationsmethoden
Eine konservative und schnelle Berechnung ist mit Miner elementar möglich. Schnell deshalb, da nach Miner elementar eine direkte Berechnung möglich ist. Konservativ deshalb, da die Dauerfestigkeit des Bauteils komplett ignoriert wird. Es werden alle Schwingspiele, egal ob oberhalb oder unterhalb der Dauerfestigkeit, als schädigend angesehen. Die Wöhlerlinie wird unterhalb der Dauerfestigkeit linear verlängert.
Ist der Nachweis danach nicht möglich, kann mit Miner konsequent gearbeitet werden. Üblicherweise lassen sich dadurch noch Festigkeitsreserven heben. Warum? Weil hier mit einem Schrittweisen Abfall der Dauerfestigkeit in Abhängigkeit der Vorschädigung durch die oberhalb der Dauerfestigkeit liegenden Schwingspiele gerechnet wird. Da die Dauerfestigkeit schrittweise abgesenkt wird, ist dafür ein iteratives vorgehen notwendig. Die Berechnung muss also mit einer Software erfolgen.
Wann lohnt sich Miner konsequent?
- wenn die Kollektivhöchstwerte nur wenig über der Dauerfestigkeit liegen
- der Nachweise nach Miner elementar nicht erfolgreich war.
5. Auf den Punkt
Ein schnellerer Nachweis der Schwingfestigkeit nach der FKM-Richtlinie ist möglich, wenn man bei der Berechnung der
- Wöhlerlinie nach den Kapiteln 2.3 bzw. 4.3, Konstruktionskennwerte und Kapitel 2.3 bzw. 4.4) und der
- Schadensakkumulation nach Miner in den Kapiteln 2.4 und 4.4
ein paar wichtige Hinweise beachtet. Der wichtigste Hinweis ist, dass konservative Annahmen getroffen werden. Konservative Annahmen können vor allem bei festigkeitssteigernden Einflüssen getroffen werden. Deshalb gilt ihnen eine besondere Beachtung.
Natürlich stellt sich dann die Frage: was tun mit der ganzen freien Zeit? Aber das kann ja jeder selber entscheiden ;).
5.1 Effiziente Berechnung der Kerbwirkungszahl Kf: Kapitel 4.3.1.2
Eine konservative und schnelle Annahme ist, dass das Bauteil ungekerbt ist (Kf = 1). In diesem Fall wird der Einfluss der Oberflächenrauheit maximal berücksichtigt. Man spart sich die Berechnung der Kerbwirkungszahl Kf.
5.2. Effiziente Berechnung der Wöhlerlinie Kapitel 4.3 und 2.3
5.2.1. Die Stützzahl nσ, Kapitel 4.3.1.3, bzw. 2.3.l.2.3
Es gibt mehrere Möglichkeiten hier Zeit zu sparen:
- Vernachlässigung der Stützzahl
- Auswahl des geeigneten Stützzahlkonzepts
- Einfache Berechnung des bezogenen Spannungsgefälles
Zu 1) Vernachlässigung der Stützzahl:
Eine konservative und schnelle Annahme ist, dass die Stützzahl nicht wirksam ist (nσ = 1). Man spart sich dadurch die z.T. aufwändige Berechnung der Stützzahl.
Zu 2) Auswahl des geeigneten Stützzahlkonzepts
Eine konservative und effiziente Wahl des Stützzahlkonzeptes ist
- Das Stützzahlkonzept nach Stieler (nach Kapitel 4.3.1.3.1 bzw. 2.3.1.2.3.1) in wahrscheinlich 99% der Fälle.
Wann sollte dann die werkstoffmechanische Stützzahl nach Kapitel 4.3.1.3.2 bzw. 2.3.1.2.3.2 angewandt werden? Erst,
- wenn scharfe Kerben vorliegen und der Nachweis nach dem Stützzahlkonzept von Stieler nicht erfolgreich war. Oder
- wenn tatsächlich mit einem Einfluss der Bauteilgröße (und damit dem statistischen Größeneinfluss) gerechnet werden muss. Aber Achtung: die Berechnung der hoch beanspruchten Oberfläche aus der FEM ist nur mit einer geeigneten Software möglich. Eine händische Auswertung wie beim bezogenen Spannungsgefälle ist leider unmöglich.
Zu 3) Einfache Berechnung des bezogenen Spannungsgefälles
Für eine konservative und schnelle Abschätzung des Spannungsgefälle Gσ ist
- meist das normale FEM Netz von ca. 5 Elementen über dem Radius ausreichend. Gleichzeitig ist
- es konservativer, wenn über mehrere Elemente hinweg ausgewertet wird und dadurch die Auswertetiefe steigt.
Erst wenn dieser Nachweis nicht ausreichend ist, ist es ratsam, den Mehraufwand der feineren Vernetzung in Kauf zu nehmen, um den bezogenen Spannungsgefälle genau zu berechnen. Sind die Kerben sehr scharf oder muss der statistische Größeneinfluss berücksichtigt werden, sollte mit der Werkstoffmechanischen Stützzahl gerechnet werden.
5.3. Effiziente Berechnung der Schadensakkumulation, Kapitel 4.4.3.5.2 bzw. 2.4.3.5.2
Eine konservative und schnelle Berechnung ist mit Miner elementar möglich.
Wann lohnt sich dann Miner konsequent?
- wenn die Kollektivhöchstwerte nur wenig über der Dauerfestigkeit liegen
- der Nachweise nach Miner elementar nicht erfolgreich war.
5.4. Überblick
Die nachfolgende Tabelle schafft noch einmal einen Überblick in kürzester Form und gibt auch den Verweis auf die Kapitel in der Richtlinie.
| Tipps für einen effizienten Schwingfestigkeitsnachweis nach der FKM Richtlinie | |||
| Einfluss | Kapitel | Vorschlag | |
| Wöhlerlinie | Einfluss der Kerbschärfe auf die Rauhigkeit (Abschätzung der Kerbwirkungszahl Kf) | Kapitel 4.3.1.2 | Vernachlässigung der Kerbwirkungszahl |
| Stützzahl | Kapitel 4.3.1.3.1 bzw. 2.3.1.2.3.1 | Vernachlässigung der Stützzahl | |
| Auswahl Stützzahlkonzept | Kapitel 4.3.1.3.1 bzw. 2.3.1.2.3.1 | Berechnung der Stützzahl nach Stieler | |
| Berechnung Spannungsgefälle in FEM | Kapitel 4.3.1.3.1 bzw. 2.3.1.2.3.1 | Nutzung des normalen FEM Netzes (5 Elemente über dem Radius) | |
| Auswertung über mehrere Elemente hinweg | |||
| Schadensakkumulation | Auswahl der Miner-Regel | Kapitel 4.4.3.5.2 bzw. 2.4.3.5.2 | Verwendung von Miner elementar |
Weiterführende Informationen zur FKM Richtlinie und Wöhlerkurven
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Betriebsfestigkeit mit FEM
Das Seminar zur Betriebsfestigkeit gibt Ihnen einen guten Überblick über die Methoden der Betriebsfestigkeit und der FEM. Hier lernen Sie
✓ alle wichtigen Methoden kennen, um Ihre Bauteile robust auf die Betriebsfestigkeit auszulegen.
✓ Schweißverbindungen auszulegen.
✓ verstehen, welche Faktoren die Lebensdauer Ihrer Bauteile besonders stark beeinflussen.
✓ Grundlagen der Finite-Elemente-Ergebnisse (FEM) kennen, anzuwenden und zu interpretieren.
✓ Lastkollektive mit Hilfe der Rainflowzählung zu ermitteln.
✓ eine Wöhlerlinie für Ihre Bauteile rechnerisch abzuschätzen.
✓ Bauteillebensdauern mittels Schadensakkumulation zu berechnen.
✓ Dauerschwingfestigkeitsnachweise zu führen.
✓ die modernen Regelwerke wie die FKM Richtlinie zur Betriebsfestigkeitsbewertung kennen.
Seminare zur FKM Richtlinie:
Haben Sie Interesse an einer schnellen Anwendung und einem einfachen Einstieg in die komplexe FKM Richtlinie? Dann ist unsere Schulung zur FKM Richtlinie für Sie richtig.
Diese ist genau richtig für Sie, wenn Sie
✓ die FKM Richtlinie schnell anwenden möchten.
✓ Ihre FEM Ergebnisse bewerten wollen.
✓ die Hintergründe der FKM Richtlinie verstehen und üben wollen.
Weiterführende Literatur
 Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses führt Sie schnell und verständlich in die Versuche und die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auslegung Ihrer Bauteile auf die Dauerfestigketi oder Betriebsfestigkeit. Sie können dann einfach Wöhlerlinien für Ihre Bauteile berechnen.
Hilfreiche Software:

Wir haben basierend auf unserer jahrelangen Erfahrung, der Mitarbeit in den Forschungsgremien zur FKM Richtlinie und dem praktischen Arbeiten mit der Richtlinie FKMmadeEASY– die Excel-Software zur FKM Richtlinie entwickelt. Wir haben dabei speziell darauf geachtet, dass diese Software
✓ einfachst möglich bedienbar
✓ gut dokumentiert und nachvollziehbar sowie
✓ optisch ansprechend ist (es soll ja auch Spaß machen).
Überzeugen Sie sich selbst davon anhand der Testversion von FKMmadeEASY – die Excel-Software zur FKM Richtlinie
Der Autor:
Photo by John Baker on Unsplash

Sehr geehrter Herr Einbock,
vielen Dank für die geteilte Informatienen auf Ihrer Seite.
Die komplexe Inhalte sind sehr gut dargestellt und für mich etwas einfacher zu folgen als andere Quellen.
Jetzt die Frage:
σAK = σW,zd · nσ · KV · KS · KNL,E · 1 / [1+1/Kf · (1/KR – 1)] · KAK
hier bei dem KV-Randichtfaktor (Tab. 4.3.7, Seite 91 -FKM) stehen Werte >1. Das heisst dass KV als festigkeitsteigernd wirkt. Bei Ihnen auf dieser Seite steht dass KV als festigkeitmindernd wirkt.
Beziehen Sie sich hier auf FKM oder betrachten Sie wegen eingene Versuchen als festigkeitsmindernd?
Danke.
Mit freundlichen Grüßen
Ciprian David
Hallo Hr. Ciprian,
vielen Dank für den guten Hinweis!
Da haben Sie vollkommen recht! Das ist ein Versehen, ich habe dies korrigiert.
Danke für die Rückmeldung und Ihnen viel Spaß mit der Richtlinie sowie der Betriebsfestigkeit
Schöne Grüße Stefan Einbock