Warum Kerben töten und Bäume kluge Ingenieur:innen sind
 Kaum eine Konstruktion kommt ohne Kerben aus. Gleichzeitig stellen Kerben meist die Schwachstelle des Bauteils dar. In diesem Artikel wollen wir die Frage klären, warum Kerben so kritisch sind, und was wir von der Natur bei der Optimierung von Kerben lernen können.
Kaum eine Konstruktion kommt ohne Kerben aus. Gleichzeitig stellen Kerben meist die Schwachstelle des Bauteils dar. In diesem Artikel wollen wir die Frage klären, warum Kerben so kritisch sind, und was wir von der Natur bei der Optimierung von Kerben lernen können.
In diesem Artikel lernen Sie, wie
- sich Kerben auf die Spannungen im Bauteil auswirken
- sich unterschiedliche Geometrien von Kerben auswirken und
- eine optimale Kerbgeometrie aussieht
Inhalt
- Was sind Kerben
- Auswirkung von Kerben
- Warum sind Kerben tödlich
- Entstehung von Kerben (Analogie Strömung)
- Optimierung
- Vergleich der Vorschläge
- Auf den Punkt
1 Was sind Kerben?
Bauteile haben oft komplizierte Formen, um ihre Funktionen zu erfüllen. Dies zeigt sich z.B. in Querschnittssprüngen, Bohrungen oder Verrundungen. Diese Formen werden auch als Kerben bezeichnet, da Sie zu einer Spannungskonzentration führen. Kerben können eine Vielzahl von Ursachen haben. Nach folgender Abbildung werden drei Arten unterschieden. Bei der Bauteilauslegung müssen alle Arten berücksichtigt werden.
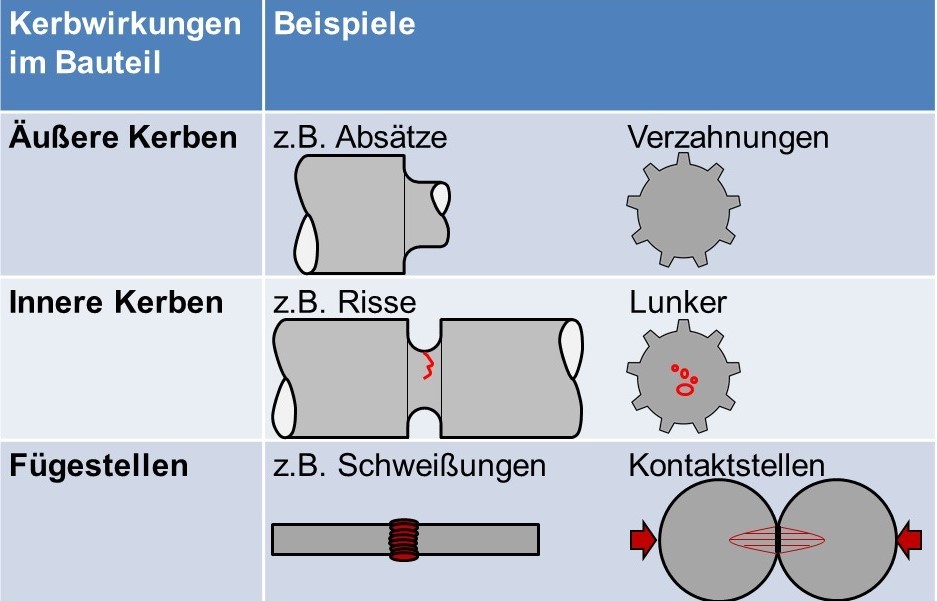
Darstellung der verschiedenen Arten von Kerben
1.1 Die äußeren Kerben
resultieren z.B. aus Verjüngungen des Bauteils. Diese Verjüngungen (Kerben) stören den gleichmäßigen Kraftfluss im Bauteil und führen zu einer Spannungskonzentration in der Kerbe. D.h. sie sind um Formzahl gegenüber den Nennspannungen erhöht.
1.2 Bei inneren Kerben
handelt es sich weitgehend um Fehler in Bauteilen, an denen sich Spannungen konzentrieren. Dies können Fertigungsfehler wie Lunker oder Einschlüsse sein. Auch Risse zählen dazu.
1.3 Fügestellen
wie Schweißnähte, Kontaktstellen oder Krafteinleitungsstellen können ebenfalls zu einer Spannungsüberhöhung führen. Bei Bauteilen, die auf Druck belastet sind (z.B. Kugellager), können sich Spannungen in Folge des Drucks / der Flächenpressung ebenfalls im Bauteilinneren konzentrieren.
2 Wie wirken sich Kerben aus?
Die Beanspruchung (Spannungen und Dehnungen) im Werkstoff können das Bauteil schädigen, wenn sie eine ausreichende Größe haben. Allgemein gilt, dass die Beanspruchung (Spannung) von der Belastung (z.B. Kräften, Momenten oder Temperaturen) und der Geometrie (Querschnitt und Kerbe) abhängt.
Bei der analytischen Berechnung von Spannungen wird zuerst die Nennspannung und dann die Kerbspannung berechnet. Die Nennspannung berücksichtigt nur den Einfluss der Belastung und der Geometrie. Bei der Kerbspannung wird auch der Einfluss der Kerbe bewertet.
Werden Spannungen mit der FEM berechnet, dann werden alle Einflüsse direkt in der Simulation berücksichtigt.
Nachfolgend wird vorgestellt, wie Nennspannungen und dann die Kerbspannungen analytisch berechnet werden.
2.1 Nennspannungen
Für den ungekerbten zylindrischen Stab unter Zugbelastung hängt die Spannung σ (Beanspruchung) von der Kraft F (Belastung) und der Querschnittsfläche A (Geometrie) ab, siehe folgende Gleichung:
σ = σnenn = F/A.
Diese Spannung wird auch als Nennspannung bezeichnet. Nennspannungen berücksichtigen den Einfluss der Belastung und der Geometrie, vernachlässigen aber die Kerbeinflüsse. Es werden vier Grundbelastungsfälle unterschieden. Zug/Druck, Biegung, Schub und Torsion. Folgende Abbildung zeigt diese.
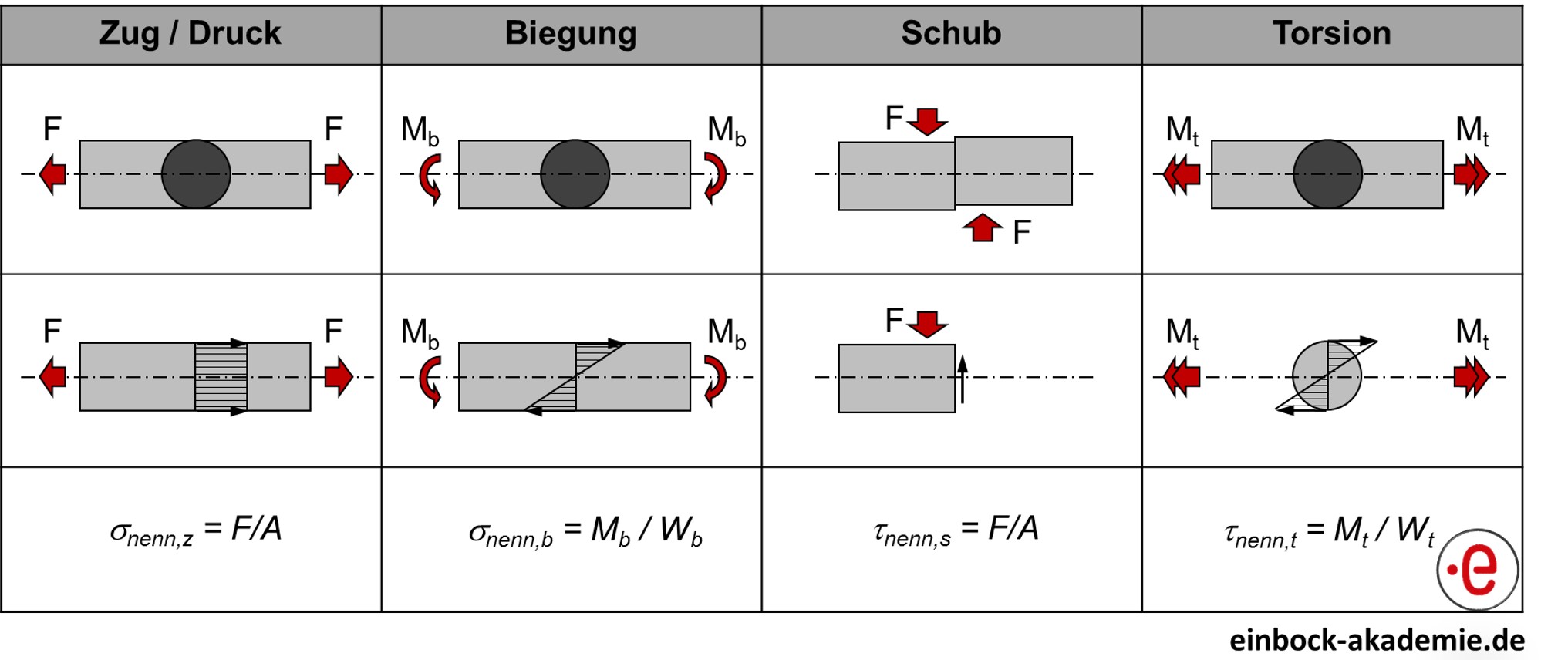
Die Berechnung von Nennspannungen für die vier Grundbelastungsfälle
Bei dem Grundbelastungsfall Zug/Druck und Schub erfolgt die Belastung durch die Kraft F, bei Biegung durch das Biegemoment Mb und bei Torsion durch das Torsionsmoment Mt. Die Geometrie wird bei Zug/Druck und Schub über die Querschnittsfläche A, bei Biegung über das Widerstandsmoment gegen Biegung Wb und bei Torsion über das Widerstandsmoment gegen Torsion Wt berücksichtigt.
2.2 Kerbspannungen
Bauteile weisen üblicherweise noch Kerben wie beispielsweise eine Verjüngung des Querschnitts, Bohrungen oder Einschnitte auf. Daraus folgt der Kerbeinfluss in Form der Formzahl Kt. Es gilt üblicherweise Kt = 1,5...5. Dieser Kerbeinfluss führt zu einer Konzentration der Spannungen in der Kerbe und damit zu einer Erhöhung der Spannung gegenüber dem ungekerbten Bauteil. Die Formzahl Kt gibt an, um welchen Faktor die Kerbspannung gegenüber der Nennspannung überhöht ist. D.h. obig Gleichung muss um die Formzahl Kt modifiziert werden, um die maximale Spannung in der Kerbe zu erhalten:
σmax = Kt * σnenn = Kt * F/A.
In folgender Abbildung ist für die Fälle Zug/Druck und Biegung der Zusammenhang zwischen Nennspannung und Kerbspannung dargestellt. Bei der Berechnung der Kerbspannungen geht man in zwei Schritten vor:
- Berechnung der Nennspannungen σnenn unter Vernachlässigung der Kerbe
- Berechnung der Kerbspannungen σmax mit Formzahlen nach folgender Abbildung.
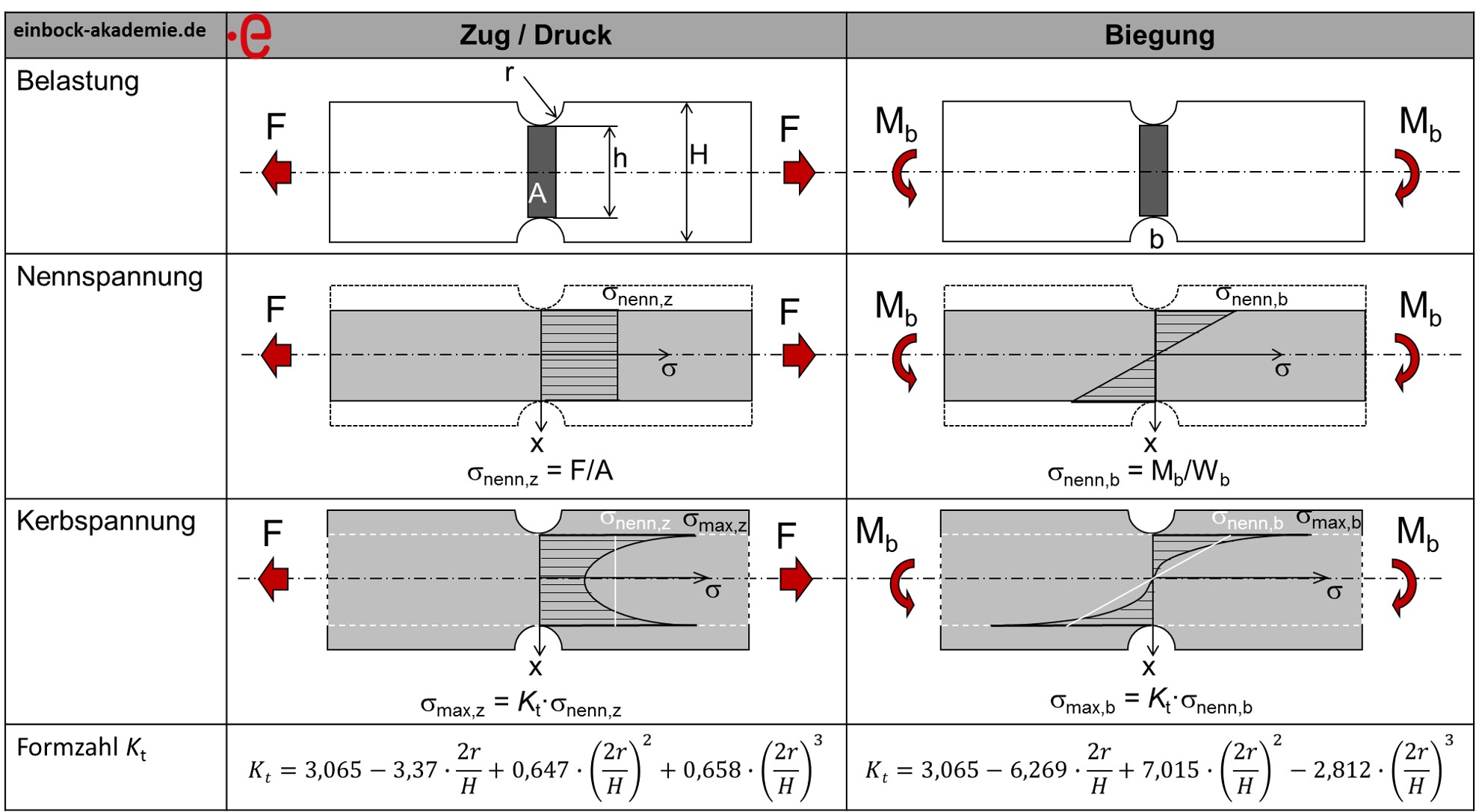
Die Berechnung von Kerbspannungen unter Berücksichtigung von Formzahlen für ausgewählte Geometrieen
Bei der Formzahl handelt es sich um eine von Geometrie und Belastungsart abhängige Größe. D.h. sie ist komplett unabhängig vom Werkstoff! Für Zug/Druck und Biegung gelten die in obigerAbbildung angegebenen Formeln. Formzahlen für weitere Geometrien sind z.B. in unserem Buch zur Betriebsfestigkeit zusammengestellt.
Alternativ zur vorgestellten Berechnung von Kerbspannungen über den analytischen Weg können diese auch mittels FEM berechnet werden. Bei linear-elastischer Berechnung ist das Ergebnis der FEM direkt die Kerbspannung
σmax = σFEM.
Etwas unintuitiv ist nach obigen Gleichungen, dass die Spannungen bei linear-elastischer Berechnung nicht vom Werkstoff abhängen! D.h., wenn die Geometrie und die Belastung dieselben sind, dann sehen Bauteile aus Kunststoff, Holz oder Stahl exakt dieselbe Spannung!
Das bedeutet andererseits, dass die Spannungen sehr gut durch eine Geometrieoptimierung reduziert werden können, und dass die Methoden dazu generell anwendbar sind.
3 Warum sind Kerben tödlich?
Weist ein Bauteil eine Kerbe auf, dann sind die Spannungen um die Formzahl höher, als bei einem ungekerbten Bauteil mit gleicher Last.
Formzahlen liegen oft im Bereich von Kt = 1,5…5. Das bedeutet näherungsweise, dass die ertragbare Belastung gekerbter Bauteile um den Faktor der Formzahl niedriger ist, als die ertragbare Belastung der ungekerbten Bauteile!
Genau diese Eigenschaft macht Kerben so tödlich, denn ein ungekerbtes Bauteil kann also um den Faktor 1,5...5 höhere Lasten aushalten. Oder es kann
- deutlich leichter sein,
- kostensparender gefertigt werden und
- länger leben.
Gleichzeitig verursacht das Entschärfen von Kerben außer Entwicklungskosten, meist keinerlei weitere Kosten.
Fazit
Es ist also fast immer lohnenswert, Kerben so gut es geht zu entschärfen.
4 Wie entstehen Kerben? Ein Erklärungsmodell
Ein Erklärungsmodell für die Kerbwirkung liefert oft die Analogie zur Strömungslehre. Dabei stellt man sich den Körper als Strömungskanal vor. Die Strömungslinien sind dann die Kraftflüsse. An den Kerben ändern sich die Strömungsgeschwindigkeiten deutlich und damit konzentrieren sich dort die Kraftflüsse. Dies führt dann dazu, dass sich die Spannungen an der Kerbe stark konzertieren, während Sie im Kern sogar abnehmen. Siehe dazu auch folgende Abbildung:
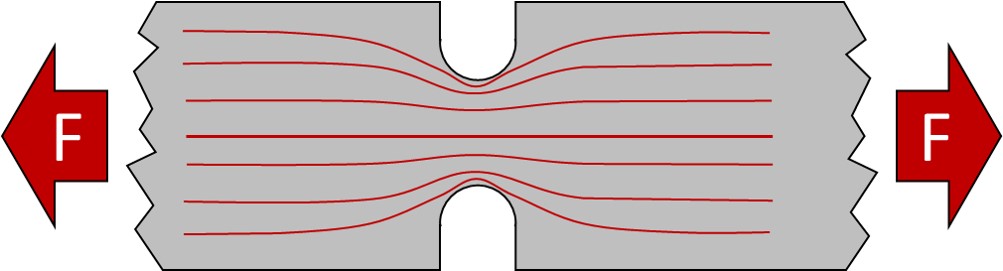
Erklärung der Kerbwirkung durch die Analogie zu Strömungslinien
Je strömungsgünstiger die Kerbe gestaltet wird, umso geringer wird dann die Änderung der Strömungsgeschwindigkeit, und damit nimmt auch die Spannungskonzentration ab, die Kerbwirkung sinkt. Das Sinken der Kerbwirkung erkennt man daran, dass die Spannungen (Strömungslinien) im Kerbquerschnitt gleich verteilt sind. Ideal ist das ungekerbte Bauteil, siehe folgendes Bild:
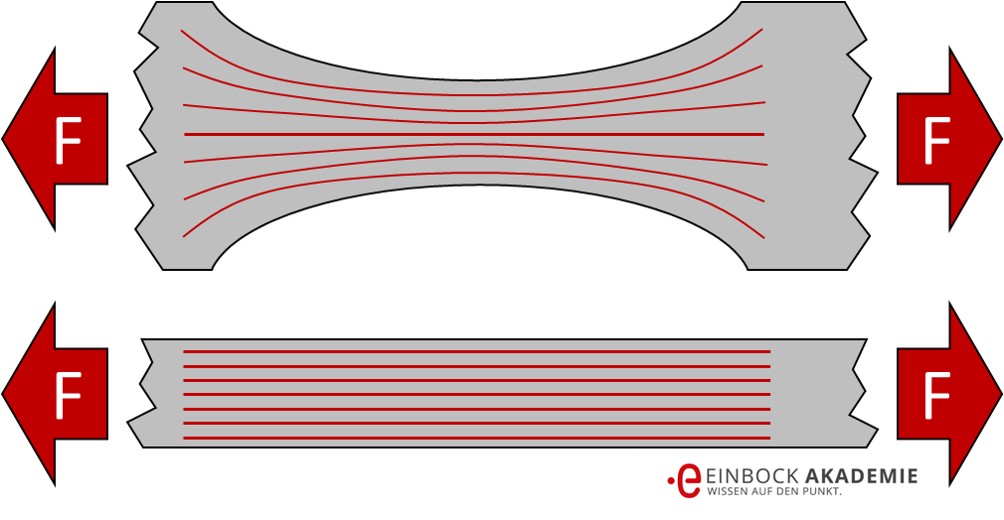
Einfluss der Optimierung von Kerben auf den Kraftfluss
Alternativ kann man auch mit Entlastungskerben arbeiten.
Dieser Gedanke hat auch zu einem Vorschlag für die Optimierung von Kerben geführt.
Fazit
Kerben lassen sich nicht vermeiden. In der Praxis sind Kerben oft sehr kritisch und können die ertragbaren Lasten massiv reduzieren. Allerdings lassen sich die Auswirkungen von Kerben (die Spannungsüberhöhung) minimieren. Dazu muss die Kerbgeometrie geschickt gewählt werden. Es gilt dabei fast immer, dass das ungekerbte Bauteil mit einer konstanten Spannung im Querschnitt die maximalen Lasten übertragen kann. Wie wir im nächsten Abschnitt sehen werden, ist der Radius als Kerbgeometrie nicht die ideale Lösung.
5 Optimierung von Kerben
Die Möglichkeiten und die Potenziale der Kerboptimierungen sollen an einem einfachen Beispiel aufgezeigt werden. Dazu werden vier Vorschläge gemacht, mit FEM berechnet und die Ergebnisse diskutiert.
5.1 Beispielbauteil
Als Beispielbauteil dient eine einfache Schulter eines Flachstabs nach folgender Abbildung. Gesucht ist die ideale Geometrie. Um diese zu finden, wird der Übergang zwischen den beiden Querschnitten der Breite D und d durch 4 verschiedene Geometrien abgebildet.
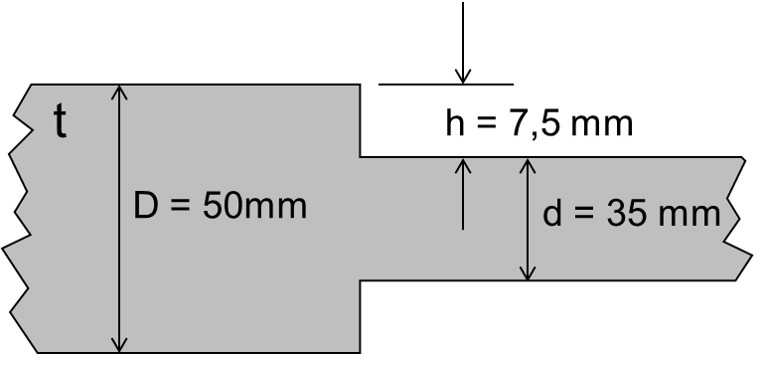
Beispielbauteil: abgesetzter Zugstab
5.2 Ingenieursvorschlag
Der Klassiker einer Kerbgeometrie ist der Kerbradius. Dazu wird die Kerbe einfach mit einem konstanten Radius ausgerundet. Diese Geometrie hat den Vorteil, dass sie die Kerbschärfe reduziert, einfach herstellbar ist, gut in Zeichnungen eingetragen werden kann und verständlich ist. Nachteilig ist, dass dieser Geometrie aus Festigkeitssicht keinerlei wissenschaftliche Begründung zu Grunde liegt. Es ist ein rein pragmatischer Vorschlag. Im vorliegenden Beispiel wird als Radius r = 5 mm gewählt.
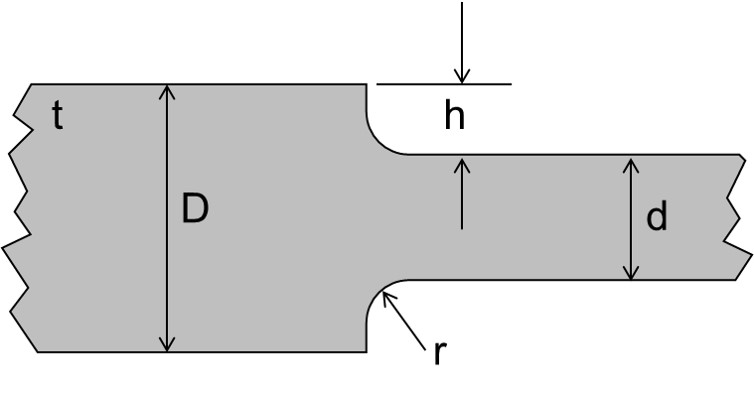
Optimierung der Kerbe durch einen Radius (Ingenieursvorschlag, r = 5 mm)
Fazit:
Der Kerbradius ist besser, als kein Radius! Und je größer der Radius gewählt wird, umso besser. Allerdings gibt es optimalere Konturen, siehe folgende Abschnitte.
5.3 Vorschlag von Baud
Ein sehr alter Vorschlag von 1935 stammt von Hr. Baud in dem Bericht: Beiträge zur Kenntnis der Spannungsverteilung in prismatischen und keilförmigen Konstruktionselementen mit Querschnittsübergängen
Hr. Baud entwirft folgende Idee. Die ideale Kontur ist gefunden, wenn sich die Spannungen entlang der Oberfläche nicht ändern, also konstant bleiben. Durch theoretische Überlegungen kommt er zu folgendem Schluss als ideale Kerbkontur.
Er stellt sich die Oberfläche im Bereich der Kerbe als mathematisch Funktion vor. Mit Hilfe dieser Funktion wird im Falle des Flachstabes der Übergang vom großen zum kleinen Bereich beschrieben. Als ideale Funktion wird eine Funktion angesehen, die asymptotisch in den schmalen Bereich und gleichzeitig horizontal in den breiten Bereich übergeht. Eine solche Funktion liefert die Stromlinie, einer aus einem Gefäß ausströmenden reibungsfreien Flüssigkeit, siehe folgende Abbildung.
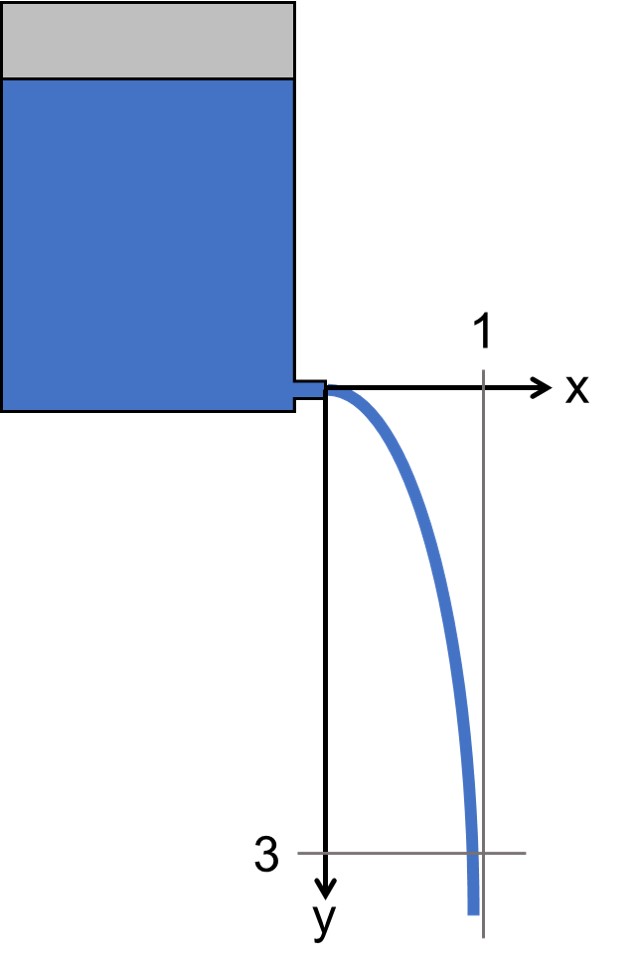
Herleitung der Kerboptimierung nach Baud am Beispiel der Ausströmung einer Flüssigkeit aus einem Tank
Die Gleichung dieser Kontur ist folgende:
y = ½ ln((1+(2x-x2)1/2)/(1-(2x-x2)1/2)) - (2x-x2)1/2
Die Umkehrfunktion ist:
x =½ ln((1+(2y-y2)1/2)/(1-(2y-y2)1/2)) - (2y-y2)1/2
Diese Gleichung ist normiert angegeben. D.h. sie gilt nur für y-Werte von 0…1. Bei etwa x = 3 nimmt sie einen asymptotischen Verlauf an.
Bestätigt wurde diese Kontur durch experimentelle Ergebnisse in der Art, dass Baud diese Kontur nachmodelliert hat, und dann für diese Kontur die Spannungen gemessen hat. Im Ergebnis hat er kaum noch eine Spannungsüberhöhung festgestellt.
Aus diesen Überlegungen heraus wird ersichtlich, dass der Kerbradius nicht die ideale Funktion ist. Die Kontur für den Flachstab sieht dann folgendermaßen aus:
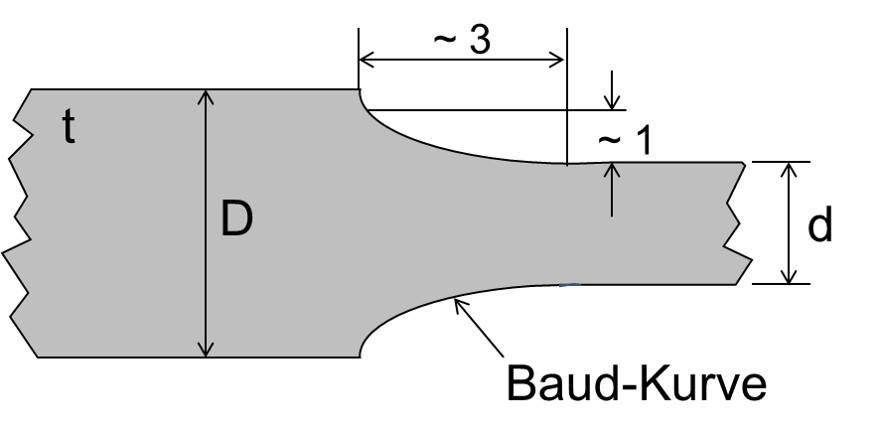
Vorschlag von Baud zur Optimierung der Kerben
Fazit:
Für die Ausrundung einer Kerbe (Flachstab) sollte etwa 3 mal so viel Platz in axialer Richtung genutzt werden, wie in in Richtung der Stabbreite.
5.4 Pragmatische Idee – die Ellipse
Eine pragmatische Idee ist die Verwendung einer Ellipse als Kerbkontur. Denn auch hier ändert sich die Krümmung stetig, auch wenn diese am schmalen Ende des Kerbstabs nicht asymptotisch in den schmalen Bereich des Stabes übergeht. Vorteilhaft ist, dass die Ellipse eindeutig bemaßt werden kann.
Die Geometrie zeigt folgende Abbildung:
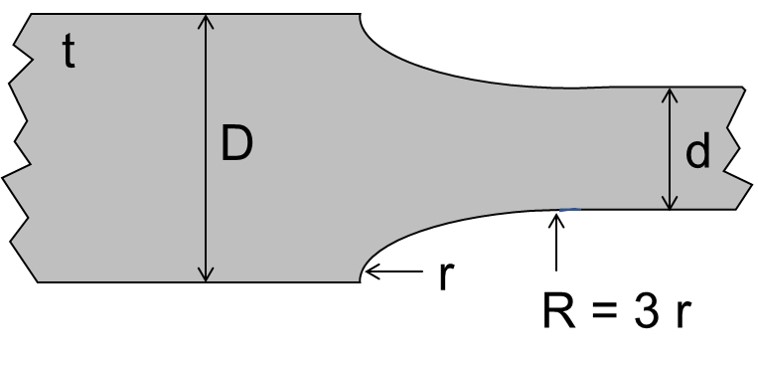
Kerboptimierung mit Hilfe einer Ellipse
Die Gleichung einer Ellipse ist folgende:
x²/R² + y²/r² = 1
Mit den Radien r und R.
Fazit:
Ausgehend von den Erfahrungen bei der Baud-Kurve wird für den Radius R vorgeschlagen:
R = 3 ⋅ r.
5.5 Vorschlag von Mattheck
Eine biologische Erklärung für die ideale Kerbgeometrie liefert Mattheck, z.B. über seine biologische Wachstumsregel. Diese besagt im Wesentlichen folgendes:
Biologische Strukturen sind bestrebt, sich kerboptimal zu bilden, sofern Sie größeren mechanischen Lasten ausgesetzt sind. Dabei gibt es prinzipiell zwei Möglichkeiten:
- an Bereichen mit hoher Beanspruchung wird Material aufgebaut (Beispiel: Baumwachstum), und/oder
- an Bereichen mit niedriger Beanspruchung wird Material abgebaut (Beispiel: Knochenwachstum).
Aus dieser Überlegung heraus leitete Hr. Mattheck seine Methode der Zugdreiecke ab. Mit Hilfe dieser Methode kann ein Konstrukteur auf einfache Art eine ideale Kerbgeometrie zeichnerisch ermitteln. Dazu wird mit mehreren Dreiecken eine Kontur erzeugt (siehe die roten Linien in folgender Abbildung). Durch diese Linien wird dann eine Kurve gelegt, welche die Kerbform darstellt. Die Erklärung dieser Methode wird in seinem Buch „Warum alles kaputt geht: Form und Versagen in Natur und Technik. Forschungszentrum Karlsruhe GmbH"* beschrieben. Der Vorschlag ist recht elegant. Die Kontur dazu zeigt folgende Abbildung.
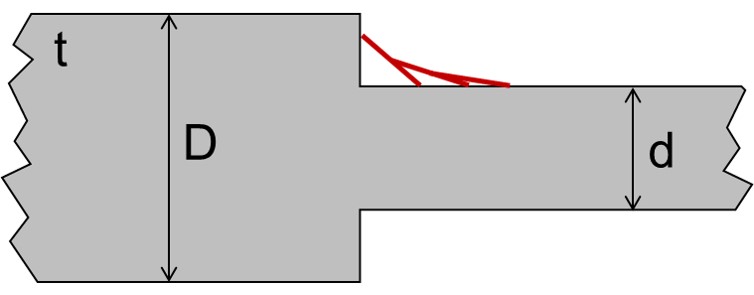
Kerboptimierung nach dem Vorschlag von Mattheck
Warum sind biologische Strukturen bestrebt ihre Formen kerboptimal zu gestalten? Eine Theorie besagt, dass das Wachstum viel Energie kostet, und dass deshalb nur an Stellen ein Wachstum stattfindet, an denen das Material wirklich gebraucht wird. Gleichzeitig wird dadurch Gewicht gespart, was z.B. im Falle von Knochen dazu führt, dass Bewegungen energieeffizienter sind, da weniger Gewicht bewegt werden muss. Anderseits bietet dieses Wachstum Flexibilität, da auf die Umwelteinflüsse wie Sonneinstrahlung, Windlasten, … optimal reagiert werden kann.
Auch der VDI hat eine Richtlinie herausgegeben, in welcher die Optimierung von Bauteile bezüglich der Festigkeit (Strukturmechanik) behandelt wird:
VDI 6224 Blatt 2:2012-08: Bionische Optimierung - Anwendung biologischer Wachstumsgesetze zur strukturmechanischen Optimierung technischer Bauteile
Beispiele für optimierte Kerben in der Natur finden sich z.B. in Knochen, Bäumen, Blättern,...
Fazit:
Aus der Bionik gilt es möglichst sanfte Übergänge zu erhalten. Daher auch das Axiom: was gut aussieht ist auch gut.
6 Vergleich der Vorschläge
Um die Auswirkung von Kerben zu zeigen, werden alle Methoden miteinander verglichen. Dies geschieht an der folgenden Geometrie des Flachstabs (mit den Abmessungen D = 50 mm und d = 35 mm von folgender Abbildung):
- Kerbradius (Viertelkreis)
- Baud-Kurve
- Ellipse
- Methode der Zugdreiecke nach Mattheck
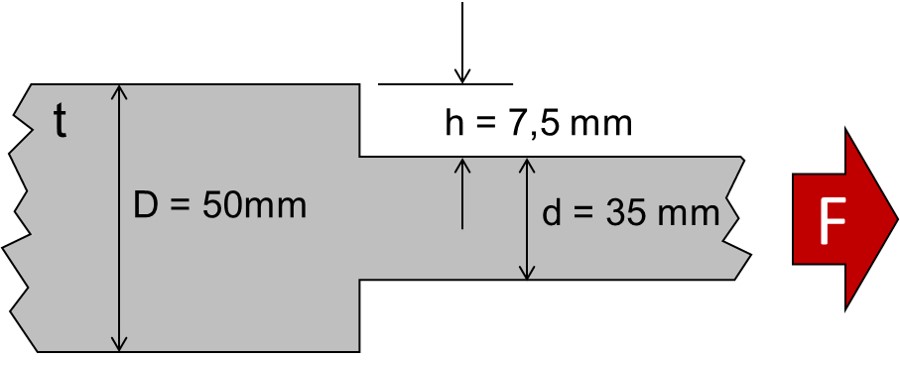
Beispielbauteil: abgesetzter Zugstab mit Zugbelastung
Für einen fairen Vergleich wurde bei allen Geometrien der Abstand D gleichgelassen. Für den Viertelkreis ergibt sich ein Radius von 5 mm. Die Abmessungen der Ellipse sind r = 5 mm und R = 15 mm. Das entspricht auch etwa der Dimension der Baud-Kurve.
Die Ergebnisse der FEM Berechnung zeigt folgende Abbildung. Hier finden Sie Hinweise zur Vernetzung einer Kerbe in einer FEM Berechnung. Bei allen Ergebnissen wurde für einen fairen Vergleich die Skala der Spannungen gleich gelassen. Als Referenz dient die Skala der Ergebnisse des Viertelkreises.
6.1 Zusammenfassung der Ergebnisse
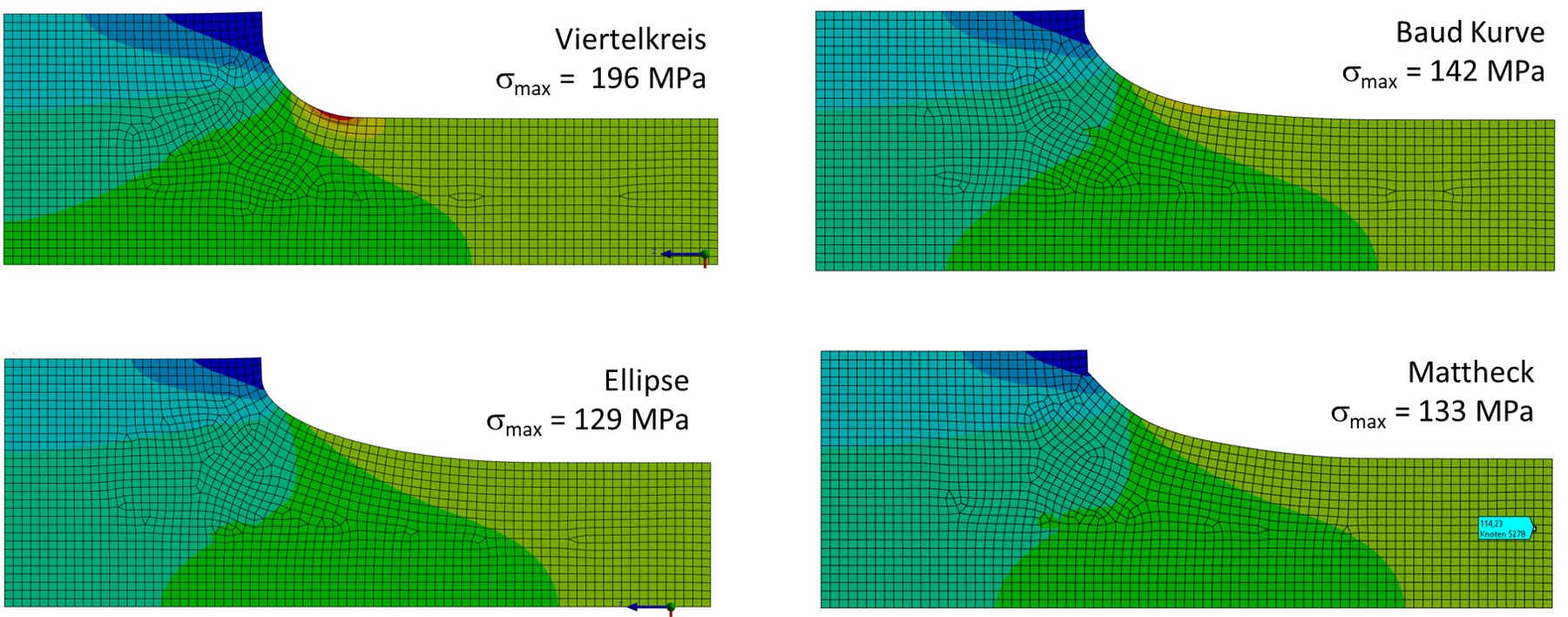
Vergleich verschiedener Verfahren zur Kerboptimierung
Folgende Tabelle fasst die Ergebnisse noch einmal zusammen:
| Ausführung der Kerbe | Spannung | Formzahl Kt | Verbesserung | |
| Formzahl | Spannung | |||
| Nennspannung σnenn: | 114 [MPa] | 1,00 | - | - |
| Kerbspannung Radius σmax,Radius: | 196 [MPa] | 1,72 | - | - |
| Kerbspannung Baud σmax,Baud: | 142 [MPa] | 1,25 | 65% | -37% |
| Kerbspannung Ellipse σmax,Ellipse: | 129 [MPa] | 1,13 | 82% | -52% |
| Kerbspannung Mattheck σmax,Mattheck: | 133 [MPa] | 1,16 | 77% | -47% |
6.2 Diskussion der Ergebnisse
In obiger Tabelle werden alle Spannungen noch einmal zusammengefasst. Die Nennspannung σnenn ist dabei die Spannung, welche sich ergibt, wenn man keine Kerbwirkung annimmt. Damit ist die Nennspannung die niedrigste Spannung, welche theoretisch möglich ist.
Außerdem werden die Formzahlen Kt für alle Geometrieen berechnet. Die Formzahl gibt an, um welchen Faktor die maximale Spannung in der Kerbe über der Nennspannung liegt. Sie besagt also, wie scharf die Kerbe ist. Eine Formzahl von Kt = 1,7 bedeutet folgendes:
- die Spannungen in der Kerbe sind um den Faktor 1,7 höher als die Nennspannungen
- 70% der Spannungen entstehen nur durch die Kerbe, nicht durch das Übertragen der Kraft. Diese Anteile der Spannungen sind sozusagen Verluste beim Übertragen der Last.
- durch das Entschärfen der Kerbe (Reduktion der Formzahl auf Kt = 1) ergibt sich ein Potenzial von 70% um die Spannung zu reduzieren. Dadurch könnte
- die übertragbare Kraft um ca. 70% erhöht, oder
- das Bauteil um ca. 70% leichter gebaut werden, oder
- die Lebensdauer des Bauteils deutlich größer sein.
Für die simulierten Geometrien zeigt sich, dass der Radius als Kerbgeometrie zu den höchsten Spannungen von σmax,Radius = 196 MPa führt. Im Vergleich dazu sind alle anderen Geometrien mit optimierten Kerben deutlich besser. in dieser Untersuchung schneiden die Ellipse und der Vorschlag von Mattheck etwa vergleichbar ab. Die Baudkurve etwas schlechter.
Realistisch lassen sich in diesem Fall die Formzahlen von Kt = 1,7 auf Kt = 1,15 reduzieren. Das entspricht immerhin einer Verbesserung von fast 50% gegenüber dem Radius!
Um diese Potenziale heben zu können, muss jedoch eine kleine Kröte geschluckt werden. Im Vergleich zum Radius muss in axialer Richtung mehr Material verbaut werden. Wenn dies möglich ist, dann sind diese Methoden sehr wirkungsvoll. Vorteilhaft ist außerdem, dass die Optimierungsmethoden unabhängig vom Werkstoff sind.
7 Auf den Punkt
Aus den obigen Untersuchungen lassen sich ein paar Schlüsse ziehen:
- Kerben sind immer potenziell tödlich, da sich hier Spannungen stark konzentrieren können!
- Es lohnt sich fast immer Kerben zu entschärfen, da dies nahezu Kostenneutral möglich ist
- Optimale Kerben bieten hohe Leichtbau-, Kosten- oder Lebensdauerpotenziale
- Hinweise zur optimalen Kerbgeometrie sind unabhängig vom Werkstoff
- Super ist es, wenn man sich an der Natur orientiert
- zur Optimierung von Kerben ist oft ein hoher Ingenieursaufwand nötig
- es gilt: was gut aussieht ist auch gut
- gut ist eine Geometrie nach Baud
- alternativ auch eine Ellipse mit dem Radienverhältnis von etwa 1/3
- die Ellipse bietet eine gute pragmatische Lösung
- die Methode von Mattheck ist gut geeignet für Konstrukteure und liefert ein schönes Verständnis zur Optimierung.
Haben Sie Mut, Kerben zu entschärfen und mit neuen Kerbgeometrien zu spielen. Die Erfahrung zeig, dass es sich fast immer lohnt und gleichzeitig auch Spaß macht, wenn man die Erfolge sieht!
Weiterführende Informationen zur Auswertung von Wöhlerversuchen
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren und Büchern. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Betriebsfestigkeit mit FEM
Das Seminar zur Betriebsfestigkeit gibt Ihnen einen guten Überblick über die Methoden der Betriebsfestigkeit und der FEM. Hier lernen Sie
- alle wichtigen Methoden kennen, um Ihre Bauteile robust auf die Betriebsfestigkeit auszulegen.
- Schweißverbindungen auszulegen.
- verstehen, welche Faktoren die Lebensdauer Ihrer Bauteile besonders stark beeinflussen.
- Grundlagen der Finite-Elemente-Ergebnisse (FEM) kennen, anzuwenden und zu interpretieren.
- Lastkollektive mit Hilfe der Rainflowzählung zu ermitteln.
- eine Wöhlerlinie für Ihre Bauteile rechnerisch abzuschätzen.
- Bauteillebensdauern mittels Schadensakkumulation zu berechnen.
- Dauerschwingfestigkeitsnachweise zu führen.
- die modernen Regelwerke wie die FKM Richtlinie zur Betriebsfestigkeitsbewertung kennen.
Seminare zur FKM Richtlinie:

Haben Sie Interesse an einer schnellen Anwendung und einem einfachen Einstieg in die komplexe FKM Richtlinie? Dann ist unsere Schulung zur FKM Richtlinie für Sie richtig.
Diese ist genau richtig für Sie, wenn Sie
- die FKM Richtlinie schnell anwenden möchten.
- Ihre FEM Ergebnisse bewerten wollen.
- die Hintergründe der FKM Richtlinie verstehen und üben wollen.
Weiterführende Literatur
 Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Um Bauteile betriebsfest oder dauerfest auszulegen und um die Hintergründe der FKM Richtlinie zu verstehen, bietet sich außerdem unser
Buch Betriebsfestigkeit und FEM an.
dieses führt Sie schnell und verständlich in die Versuche und die Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auslegung Ihrer Bauteile auf die Dauerfestigkeit oder Betriebsfestigkeit. Sie können dann einfach Wöhlerlinien für Ihre Bauteile berechnen.

Toller Artikel!
Gibt es eigentlich Überlegungen, wie der Übergangsradius aussehen müsste, damit an jeder Stelle die gleiche Spannung vorliegt?
Vermutung: Eine e-Funktion??
Hallo,
danke für die netten Worte! Das motiviert mich weiter zu machen!
Leider kenne ich keine weiteren konkreteren Funktionen. Falls aber Sie etwas finden, würde mich das auch interessieren.
Mittlerweile optimiert man auch oft mittels numerischer Optimierungsmethoden, so dass keine konkrete Funktion nötig ist.
Ihnen viel Freude bei der Optimierung! Das ist ein spannendes Feld!
Schöne Grüße
Stefan Einbock