Eine Einarbeitung in das Fachgebiet der Betriebsfestigkeit ist oftmals schwierig. Unter anderem wegen der Statistik. Mühsam und zeitintensiv habe ich mich in die Statistik der Betriebsfestigkeit eingearbeitet. Die Gute Nachricht ist: sie können sich diese Mühe sparen, denn dabei ist dieses Buch entstanden.
Das Buch Statistik der Betriebsfestigkeit - schnell verstehen & anwenden
- fokussiert auf die wichtigsten Methoden der Statistik ,
- bietet eine schnelle Einarbeitung in die Statistik,
- enthält verständlich geschrieben ist und viele Abbildungen,
- ermöglicht eine einfache Anwendung im beruflichen Alltag,
- behnadelt die Auswertung von Versuchen genauso wie die Berechnung von Sicherheitsfaktoren.
Dieses Buch ergänzt die theoretischen Methoden um Werkstoff- und Berechnungsdaten. Außerdem erhalten Sie kostenlos praktische Exceltools. Dadurch können Sie das Wissen direkt im beruflichen Alltag anwenden.
Um eine schnelle Einarbeitung zu gewährleisten, fokussiert dieses Buch auf die wichtigsten Methoden und beschränkt sich auf die absolut notwendige Mathematik. Zusätzlich finden Sie noch hilfreiche Tipps und Erfahrungen zu einer deutlichen Steigerung der Lerneffizienz.
Für eine verständliche Vermittlung des Inhaltes werden viele Abbildungen genutzt, die das Geschriebene untermalen. Es wird zusätzlich bewusst eine einfache, klare Sprache verwendet (der berufliche Alltag ist kompliziert genug). Zur Festigung des Verständnisses wird die Theorie außerdem durch umfangreiche praxisrelevante Übungen ergänzt.
Zur einfachen Anwendung der Methoden finden Sie nützliche Excel-Tools. Diese decken den Inhalt der wichtigsten Methoden dieses Buches ab und stehen Ihnen zum kostenlosen Download zur Verfügung. Ergänzend finden Sie umfangreiche Werkstoffdaten und Erfahrungswerte. Dies ermöglicht Ihnen eine Auslegung Ihrer Bauteile auch ohne eigene Versuche. Da die Datenauswertung oftmals mit Excel geschieht, werden für die wichtigsten Gleichungen die Excel-Formeln in folgender Form angegeben:
EXCEL: = MITTELWERT(x1, x2, ...,xn).
Dieses Buch versetzt Sie dadurch in die Lage,
- die Hintergründe zu verstehen
- Versuchsdaten (z. B. Wöhlerlinien) statistisch mit Hilfe von Wahrscheinlichkeitsnetzen und der Regression auszuwerten
- Sicherheitsfaktoren Ihrer Bauteile zu berechnen und
- den Einfluss geringer Stichprobenumfänge zu bewerten.
Ich wünsche Ihnen genauso viel Freude beim Lesen und Anwenden der Methoden, wie ich sie beim Schreiben hatte und bin auf Ihre Rückmeldungen gespannt!
Weitere Informationen finden Sie auf unserer Homepage.
Um Ihnen einen Einblick in das Buch zu geben möchte ich Ihnen das Kapitel zur Regression vorstellen.
Die Regression
Die Betriebsfestigkeit ist ein empirisches Fachgebiet. Das bedeutet, dass viele Erkenntnisse auf der Interpretation von Versuchsergebnissen beruhen. Häufig soll der Zusammenhang zwischen zwei Variablen (x und y) über Versuche ermittelt werden. Dazu wird eine Variable in einem festgelegten Bereich variiert (üblicherweise x) und die Auswirkung auf die zweite Variable (meist y) experimentell bestimmt. Bei der Variable die variiert wird spricht man von der erklärenden Variable. Die zweite Variable ist die zu erklärende Variable.
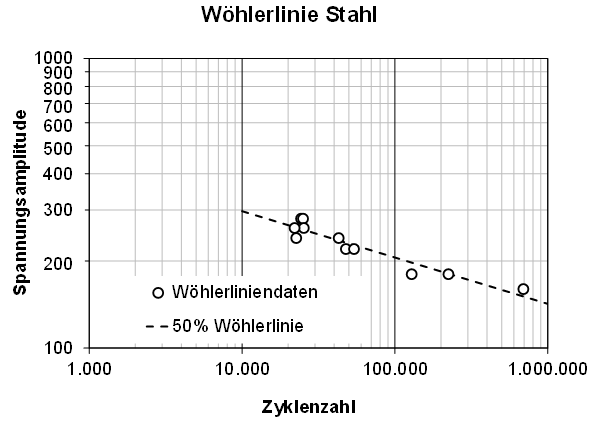
Ein Beispiel dazu ist die experimentell ermittelte Wöhlerlinie (siehe folgende Abbildung). Im Wöhlerversuch wird die Spannungsamplitude variiert. Für jede Spannungsamplitude wird so lange getestet, bis die Lebensdauer erreicht ist. In diesem Fall ist die Spanungsamplitude die erklärende Variable und die Lebensdauer die zu erklärende Variable.
Die Versuchsergebnisse streuen. Als Ergebnis liegt also eine Datenpunktwolke und kein funktionaler Zusammenhang vor. Um in diese Datenpunkt-wolke eine Ausgleichsfunktion zu legen, die den Trend beschreibt werden Regressionsmethoden verwendet.
Die Methode der kleinsten Quadrate
Nachfolgende Abbildung erklärt die Methode der kleinsten Quadrate am Beispiel einer Geraden als Ausgleichsfunktion. Vorgeschlagen wurde diese Methode erstmals durch Gauß. Es wird für jeden Datenpunkt die Abweichung der y-Koordinate dieses Punktes zur gesuchten Geraden berechnet.
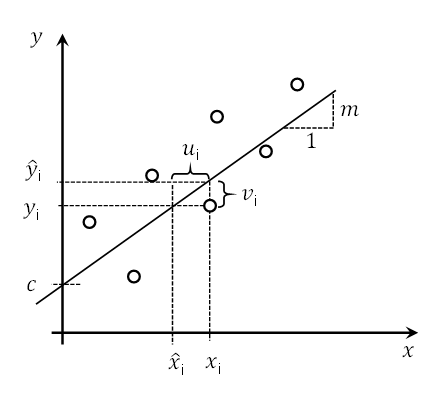
Die ideale Gerade liegt vor, wenn die Summe der quadratischen Abweichungen minimal ist:
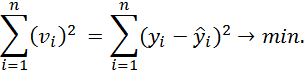 | (1) |
Soll die Datenpunktwolke durch eine Gerade angenähert werden, gilt für :
| | (2) |
Einsetzen von (2) in (1) ergibt die Summe der quadratischen Abweichungen in Abhängigkeit der Parameter und der Geradengleichung:
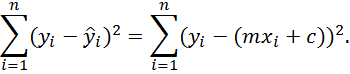 | (3) |
Durch partielles Ableiten nach und sowie Nullstellensuche ergeben sich die Parameter und der idealen Geradengleichung:
EXCEL: =STEIGUNG(y; x) | (4) |
EXCEL: =ACHSENABSCHNITT (y; x) | (5) |
mit den Mittelwerten:
EXCEL: =MITTELWERT(x)
EXCEL: =MITTELWERT(y) |
(6) |
Analog der beschriebenen Vorgehensweise lassen sich Datenpunktwolken auch durch beliebige Funktionen (z. B. Polynome) annähern. Es sind auch Ausgleichsfunktionen mit mehreren erklärenden Variablen möglich. Dafür ist dann jedoch eine Software erforderlich, dies kann Minitab sein.
Im beschriebenen Beispiel wurden die quadratischen Abweichungen in y-Richtung minimiert. Es ist auch möglich die quadratischen Abweichungen in x-Richtung zu minimieren.
Auf den Punkt:
- Bei Wöhlerlinien werden quadratische Abweichungen in x-Richtung minimiert
- Regressionsmethoden lassen sich sehr einfach mit Excel umsetzen
- komplexere Regressionen erfordern Software
Haben Sie keine Scheu vor der Statistik! Sie ist bei richtiger Anwendung jedem Ingenieur eine große Hilfe und - man glaubt es kaum - nach einiger Zeit richtig Spass! Mit unserem Buch Statistik der Betriebsfestigkeit - schnell verstehen & anwenden gelingt Ihnen ein schneller Einstieg in die wichtigsten Methoden der Statistik und Sie lernen diese richtig anzuwenden, denn:
Statistic makes a good engineer great and a bad engineer dangerous;)
