Typische Streuungen von Wöhlerlinien und Dauerfestigkeiten
Das größte Problem bei Versuchen zur Ermittlung von Werkstoffkennwerten ist der Umgang mit Streuungen, insbesondere bei kleinen Stichproben. In diesem Artikel erfahren Sie, mit welchen typischen Streuungen Sie beim Auswerten von Versuchen zur Ermittlung von Werkstoffkennwerten rechnen müssen. Natürlich in Abhängigkeit der Stichprobengröße.
In diesem Artikel lernen Sie
- Typische Streuungen von Werkstoffkennwerten (Wöhlerlinienneigung, Knickpunktzyklenzahl und Dauerfestigkeit kennen
- Warum die Stichprobe eine so große Rolle spielt
- Wie Sie Vertrauensbereiche für die Neigung, die Dauerfestigkeit und die Knickpunktzyklenzahl der Wöhlerlinie sinnvoll angeben.
Inhalt:
- Grundlagen
- Auswertung von Wöhlerversuchen
- Typische Streuungen
- Praxistipps
- Auf den Punkt
- Weitere Informationen
1. Grundlagen
In der Betriebsfestigkeit haben wir es fast immer mit Stichproben zu tun. Und gleichzeitig haben diese Stichproben meist nur einen sehr geringen Stichprobenumfang von n < 20. Mit Hilfe dieser kleinen Stichproben wird dann auf die sehr große Grundgesamtheit aller Daten geschlossen. Das bedeutet, dass die Aussagen die getroffen werden unsicher sind. Mit zunehmender Versuchszahl wird die Sicherheit der Aussage aber steigen.
Das bedeutet in der Sprache der Ingenieure:
Angenommen es wird zweimal einen Wöhlerlinien des gleichen Bauteils mit mehreren Teilen ermittelt und die Bauteile die getestet werden unterscheiden sich nur rein zufällig. Dann werden wir Wöhlerlinien erhalten, die sich bezüglich der
- Neigung k
- Dauerfestigkeit σD und
- Knickpunktzyklenzahl ND
unterscheiden. Die Unterschiede werden umso größer sein, je kleiner die Versuchsanzahl n (die Stichprobe) gewählt wurde.
Die Frage ist jetzt, wie stark können die Wöhlerlinienparameter (Neigung, Dauerfestigkeit und Knickpunktzyklenzahl) streuen, so dass man noch von einer normalen Abweichung ausgeht.
Um diese Frage zu beantworten, werden Vertrauensbereiche für die einzelnen Parameter angegeben (z. B. k = 5 +/- 1). Diese geben an, in welchem Bereich sich ein Parameter mit einer gewissen Wahrscheinlichkeit (der Vertrauenswahrscheinlichkeit von typischerweise 80%) befinden wird.
Noch einmal kurz die wichtigsten Begriffe etwas detaillierter beschrieben.
1.1 Unterschied Grundgesamtheit und Stichprobe
Bei der Grundgesamtheit handelt es sich um alle möglichen Messwerte des Merkmalswertes. Dies beinhaltet beim Beispiel der ermittelten Wöhlerlinien eines Bauteils wirklich alle möglichen Wöhlerlinien dieses Werkstoffes. Eine messtechnische / experimentelle Ermittlung der Grundgesamtheit ist auf Grund der Anzahl der nötigen Versuche im Maschinenbau praktisch nicht möglich.
Deshalb versucht auf Basis eines Versuchs an einer kleinen aber möglichst repräsentativen Anzahl an Bauteilen (der Stichprobe) auf die Grundgesamtheit aller Bauteile zu schließen.
Die Folgende Abbildung erklärt das am Beispiel der Wahlprognose. Um das Wahlergebnis einer Bundestagswahl abzuschätzen werden Umfragen zum Wahlverhalten an einem kleinen Teil aller Wahlberechtigten geführt. Die Umfrage stellt dabei die Stichprobe dar. Das Auszählungsergebnis aller abgegebener Stimmzettel ist stellt dabei die Grundgesamtheit dar.
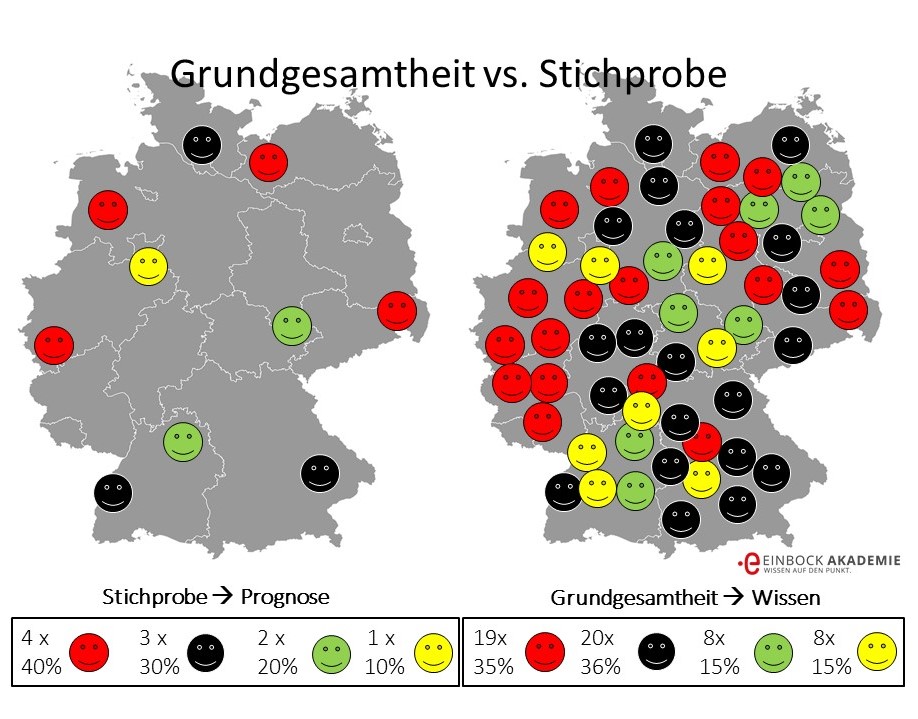
Unterschied zwischen der Stichprobe und der Grundgesamtheit
Kurz: die Stichprobe ist eine Prognose (eine Abschätzung), mit der man auf die Grundgesamtheit schließt.
Im Ergebnis wird das Ergebnis der Stichprobe von dem der Grundgesamtheit abweichen. Dies ist im Falle der Wahlen in obiger Abbildung dargestellt. Deshalb werden in der Technik Vertrauensbereiche angegeben.
Die Güte der Prognose hängt
- vom Stichprobenumfang und
- vor allem von der Repräsentativität
der Stichprobe ab. Deshalb muss der Repräsentativität der Stichprobe eine besondere Aufmerksamkeit gewidmet werden.
Kurz gesagt beschreibt die Repräsentativität, wie gut die Stichprobe die Realität widerspiegelt. Am Beispiel der Wahlprognose sollten die Befragten Wahlberechtigten einen guten Querschnitt durch die Gesellschaft darstellen (bzgl. Einkommen, Geschlecht, Wohnort, Alter,…). Am Beispiel der Betriebsfestigkeit sollten die erprobten Teile so gut wie möglich die Fertigungs-, Geometrie-, …, Medieneinflüsse wiederspiegeln.
1.2 Vertrauensbereich
Die experimentelle Ermittlung von Werkstoffkennwerten erfolgt immer auf Basis einer Stichprobe, d. h. von allen Versuchen, die theoretisch möglich wären (Grundgesamtheit) wird nur ein kleiner Teil für die Versuche verwendet (Stichprobe). Es ist davon auszugehen, dass zusätzliche Stichproben von den Werten der ersten Stichprobe abweichen werden. Es streuen also nicht nur die Ergebnisse innerhalb einer Stichprobe, sondern auch die Stichproben selbst. Die folgende Abbildung zeigt dies am Beispiel von Wöhlerversuchen.
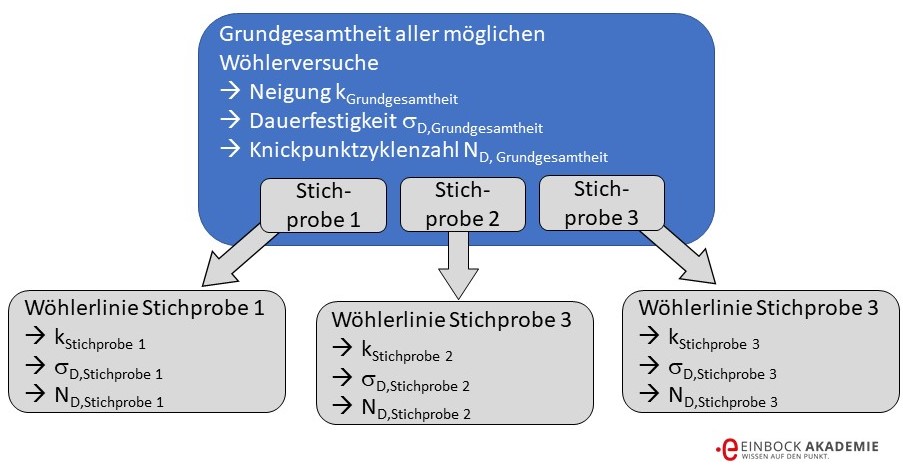
Grundgesamtheit vs. Stichprobe am Beispiel von Wöhlerlinien
Bei z.B. drei Stichproben zur Ermittlung von Wöhlerlinien der gleichen Bauteile werden sich drei unterschiedliche Kennwerte (Neigung, Dauerfestigkeit und Knickpunktzyklenzahl) ergeben. Ob diese Unterschiede noch normal sind, bewertet der Vertrauensbereich.
Üblicherweise wird der Vertrauensbereich für eine Vertrauenswahrscheinlichkeit von PA = 80% angegeben. In diesem Fall liegt der wahre Wert der der Wöhlerlinie mit einer Wahrscheinlichkeit von 80% innerhalb des Vertrauensbereich.
2. Auswertung von Wöhlerversuchen
Bei der Auswertung von Wöhlerversuchen werden zuerst die Versuchspunkte in ein doppellogarithmisches Netz eingetragen (siehe oberes Bild in folgender Abbildung). Anschließend werden die Ergebnisse statistisch ausgewertet und eine mittlere Neigung k, Knickpunktzyklenzahl ND und Dauerfestigkeit σD berechnet und eingezeichnet. In unserem Artikel zur statistischen Auswertung von Dauerfestigkeiten nach dem Treppenstufenverfahren finden Sie weitere Details zur Auswertung der Dauerfestigkeit. Für die Auswertung und Versuchsführung im Bereich der Zeitfestigkeit von Wöhlerlinien hilft ihnen dieser Artikel evtl. weiter.
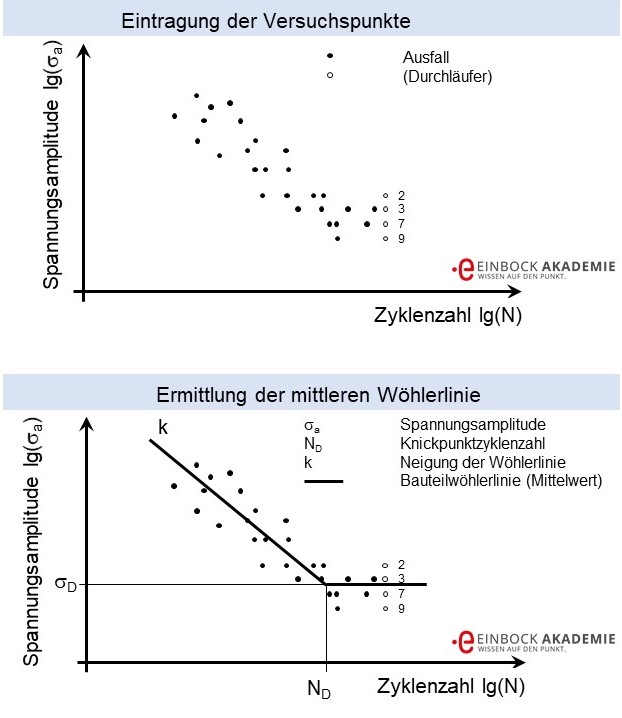
Auswertung von Wöhlerlinien
In seiner Promotion zur statistischen Auswertung von Wöhlerversuchen, die auch als Basis der neuen DIN 50100 diente hat Hr. Dr. Müller sich genau diesem Thema gewidmet. In den nachfolgenden Abschnitten werden diese Ergebnisse kurz dargestellt.
Für die folgenden Aussagen wird von einem normalen Stichprobenumfang von folgenden Randbedingungen ausgegangen:
- etwa 10..20 Teilen mit einer guten Verteilung der Versuche im Zeitfestigkeitsgebiet,
- normalen Werkstoffen (maschinenbautypische Werkstoffe mit den dort üblichen Streuungen wie z.B. in unserem Artikel zur Sicherheit der Dauerfestigkeit bezüglich der Dauerfestigkeit, die logarithmische Standardabweichung ist bei etwa s = 0,05) ausgegangen,
- eine Vertrauenswahrscheinlichkeit von 80%
3. Typische Streuungen
Im Ergebnis der oben genannten Annahmen können folgende typische Streuungen für die Wöhlerlinienparameter angegeben werden:
| Logarithmische Standardabweichung s = 0,05 | ||
| Stichprobenumfang n = 10 | Stichprobenumfang n = 20 | |
| Dauerfestigkeit sD | σD,GG = σD,ST/1,08 … σD,ST*1,08 | σD,GG = σD,ST/1,06 … σD,ST*1,06 |
| Neigung k | kGG = kST/1,55…kST*1,55 | kGG = kST/1,38…kST*1,38 |
| Knickpunktzyklenzahl ND | ND,GG = ND,ST /2,3…ND,ST*2,3 | ND,GG = ND,ST /2,0…ND,ST*2,0 |
Es gelten folgende Abkürzungen:
- GG: Grundgesamtheit
- ST: Stichprobe
Für typische Werte der Neigung und der Knickpunktzyklenzahl der Wöhlerlinie von
- k = 5
- ND = 106
ergeben sich folgende Streuungen:
| Logarithmische Standardabweichung s = 0,05 | ||
| Stichprobenumfang n = 10 | Stichprobenumfang n = 20 | |
| Dauerfestigkeit sD | σD,GG = σD,ST/1,08 … σD,ST*1,08 | σD,GG = σD,ST/1,06 … σD,ST*1,06 |
| Neigung k | kGG = kST/1,55…kST*1,55 = kGG = 5/1,55…5*1,55 kGG = 3,22…7,75 | kGG = kST/1,38…kST*1,38 kGG = 5/1,38…5*1,38 kGG = 3,62…6,9 |
| Knickpunktzyklenzahl ND | ND,GG = ND,ST /2,3…ND,ST*2,3 ND,GG = 106 /2,3…106 *2,3 ND,GG = 4,3 * 105… 2,3 * 106 | ND,GG = ND,ST /2,0…ND,ST*2,0 ND,GG = 106 /2,0…106 *2,0 ND,GG = 5 * 105… 2,0 * 106 |
Werden also die Kennwerte zweier Wöhlerlinien des gleichen Bauteils miteinander verglichen, dann müssen die oben genannten Streuungen berücksichtigt werden. Es ist also durchaus normal, wenn die Knickpunktzyklenzahl der beiden Wöhlerversuche um den Faktor +/- 2 unterscheiden. Auch bei der Neigung der beiden Wöhlerlinien muss mit typischen Streuungen von etwa k = 3,5…7,5 gerechnet werden.
Deshalb sollten bei der Auswertung von Wöhlerversuchen diese typischen Vertrauensbereiche immer mit angegeben oder zumindest im Hinterkopf behalten werden.
3. Praxistipp:
Allgemein gilt:
- Geben Sie bei der Auswertung von Wöhlerversuchen diese typischen Vertrauensbereiche immer mit an. Oder behalten Sie diese zumindest im Hinterkopf
- Insbesondere bei Vergleichen zwischen zwei Versuchen sollten die typischen Streuungen berücksichtigt werden, um nicht voreilig falsche Schlüsse zu ziehen.
4. Auf den Punkt:
- Alle Versuche der Betriebsfestigkeit wie z.B. Wöhlerlinien werden an relativ kleinen Stichproben durchgeführt.
- Aus diesen Versuchen werden die Wöhlerlinienkennwerte wie Neigung, Knickpunktzyklenzahl und Dauerfestigkeit abgeleitet.
- Da es sich bei den Versuchen um relativ kleine Stichproben handelt, können die Wöhlerlinienkennwert nur mit einer gewissen Unschärfe ermittelt werden.
- Deshalb sollten bei der Auswertung von Wöhlerversuchen die typischen Vertrauensbereiche für eine Vertrauenswahrscheinlichkeit von ca. 80% angegeben werden.
- Üblich sind hier die folgenden Streuungen:
| Logarithmische Standardabweichung s = 0,05 | ||
| Stichprobenumfang n = 10 | Stichprobenumfang n = 20 | |
| Dauerfestigkeit sD | σD,GG = σD,ST/1,08 … σD,ST*1,08 | σD,GG = σD,ST/1,06 … σD,ST*1,06 |
| Neigung k | kGG = kST/1,55…kST*1,55 = kGG = 5/1,55…5*1,55 kGG = 3,22…7,75 | kGG = kST/1,38…kST*1,38 kGG = 5/1,38…5*1,38 kGG = 3,62…6,9 |
| Knickpunktzyklenzahl ND | ND,GG = ND,ST /2,3…ND,ST*2,3 ND,GG = 106 /2,3…106 *2,3 ND,GG = 4,3 * 105… 2,3 * 106 | ND,GG = ND,ST /2,0…ND,ST*2,0 ND,GG = 106 /2,0…106 *2,0 ND,GG = 5 * 105… 2,0 * 106 |
Weiterführende Informationen zur Auswertung von Wöhlerversuchen
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren und Büchern. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Werkstoffkennwerte der Betriebsfestigkeit (für Simulation und Auslegung) einfach ermitteln und anwenden
Wollen Sie Ihre Versuche so kostengünstig wie möglich und mit der geringsten Anzahl an Versuchen durchführen? Dann ist evtl. unsere Wöhlerlinien auswerten und Versuche planen für Sie richtig.
Sie lernen hier,
- wie Sie Wöhlerversuche und Dauerfestigkeitsversuche mit geringst möglichem Stichprobenumfang durchführen
- Wöhlerlinien und Dauerfestigkeiten statistisch auszuwerten
- Ausreißer zu finden und mit Ausreißern umzugehen
- Versuche aus der Vergangenheit zu nutzen
- mit sehr geringen Stichprobenumfängen umzugehen
- Sicherheiten für Ihre Bauteilauslegung abzuleiten
- zwei Wöhlerlinien statistisch miteinander zu vergleichen
- einen kurzen Einstieg in die Betriebsfestigkeit kennen.
Weiterführende Literatur

Um Wöhlerkurven und Dauerfestigkeiten statistisch auszuwerten und zu planen, bietet sich außerdem unser Buch Statistik der Betriebsfestigkeit an.
dieses führt Sie schnell und verständlich in die Versuche und die Statistik Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auswertung von Versuchen der Betriebsfestigkeit wie Wöhlerlinien.
Der Autor:
Bild von Thorsten Frenzel auf Pixabay
Lizenz: CC0 1.0
