Sind die Unterschiede zwischen zwei Wöhlerversuchen zufällig oder Signifikant? Wir stellen einen geeigneten statstischen Test vor.
Die Ergebnisse von Wöhlerversuchen streuen immer. Zusätzlich müssen Wöhlerversuche immer als eine Stichprobe angesehen werden. Daraus folgt, dass sich zwei Versuche auch desselben Werkstoffes voneinander unterscheiden werden. In diesem Artikel erfahren Sie, wie Sie mit dem t-Test einfach testen können, ob diese Unterschiede zufällig oder signifikant sind.
Empirische Daten streuen. Um Unterschiede oder zusammenhänge bewerten zu können, werden statistische Tests eingesetzt. Ziel der statistischen Tests ist es, aus einer Datenmenge mit Hilfe statistischer Methoden eine Hypothese zu bestätigen oder zu wiederlegen, also eine Entscheidung zu treffen. Wir müssen uns hier immer vor Augen halten, dass absolute Aussagen nicht möglich sind, aber Handlungsrichtlinien gut gegeben werden können.
Beispiele für statistische Tests…
…sind:
- Es soll überprüft werden, ob eine bestimmte Charge produzierter Teile ist Ausschuss ist und damit gesperrt werden muss, oder nicht.
- Die ermittelten Lebensdauern liegen unter einem Grenzwert. Es soll überprüft werden, ob die Unterscheide zufällig sind, oder nicht.
- Werden auf drei Prüfständen im Mittel die gleichen Ergebnisse gemessen oder nicht?
Da die Aussagen auf empirischen (also streuenden) Daten beruhen, sind absolute Aussagen nicht möglich. Jede Aussage ist somit fehlerbehaftet. Die Größe des Fehlers wird als Signifikanz α bezeichnet und kann eingestellt werden.
Um in dieses Thema einzusteigen wird der Statistisch Test erst an einem einfachen Beispiel aus dem Alltag erklärt (einem Gerichtsprozess). Dann im zweiten Schritt wird ein statistischer Test (der t-Test) an folgendem konkreten Beispiel dargestellt.
Es wurden zwei Wöhlerversuche des gleichen Werkstoffes aber einer unterschiedlichen Charge auf demselben Lastniveau durchgeführt. Die Frage ist: unterscheiden sich die beiden Chargen im Mittel voneinander?
Der statistische Test am Beispiel des Gerichtsverfahrens…
…einfach erklärt. Ein Gerichtsverfahren soll eine Aussage treffen, ob der Angeklagte für schuldig befunden oder freigesprochen wird. Dabei gilt der Grundsatz der Unschuldsvermutung in rechtsstaatlichen Verfahren. Das bedeutet, dass von der Unschuld des Angeklagten ausgegangen wird. Durch die Beweisführung muss also die Schuld des Angeklagten nachgewiesen werden. Die Entscheidung des Gerichts ist eine entweder – oder Entscheidung zwischen zwei Hypothesen (Annahmen). Also entweder ist der Angeklagte unschuldig (Hypothese 1) oder schuldig (Hypothese 2).
Am Ende eines Urteils wird entweder die Entscheidung
- der Angeklagte ist schuldig, oder
- der Angeklagte ist nicht schuldig
getroffen. Bemerkenswert ist dabei, dass im zweiten Falle von „nicht schuldig“ gesprochen wird und nicht von „unschuldig“. Diese Aussage drückt die Unsicherheit des Gerichtes bei der Urteilssprechung aus.
Es gibt eine Vielzahl an statistischen Tests. Bei der Auswahl hilft der von mir entwickelte Assistent zur Testauswahl:
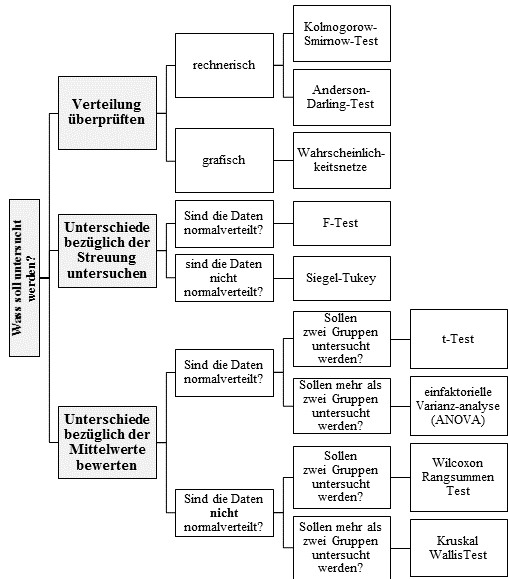
Assistent zur Auswahl des geeigneten statstischen Tests abhängig von der Fragestellung
Die Hypothesen (Nullhypothese und Alternativhypothese):
In der Statistik wird die erste Hypothese (Angeklagter ist unschuldig) als Nullhypothese H0 bezeichnet. Die zweite Hypothese (Angeklagter ist schuldig) wird als Alternativhypothese H1 bezeichnet (Angeklagter ist schuldig). Die Nullhypothese (Angeklagter ist unschuldig) wird erst verworfen, wenn die Wahrscheinlichkeit eines Irrtums (fälschliche Anklage) sehr klein wird. Diese Wahrscheinlichkeit heist in der Statistik Signifikanz α und der Fehler der falschen Anklage heist Fehler erster Art. Leider steigt dadurch die Wahrscheinlichkeit, dass aus Mangel an Beweisen, der Angeklagte doch schuldig ist, dies aber nicht bewiesen werden kann. Dieser Fehler (Angeklagter ist trotz Freispruch schuldig) heist in der Statistik Fehler zweiter Art und hat die Wahrscheinlichkeit β (vergleich auch folgenden Artikel Link). In der Technik sind folgende Wahrscheinlichkeiten üblich:
α = 5%
β = 20%.
Das bedeutet im Falle des Gerichtsprozesses, dass jeder 20te angeklagte fälschlicherweise verurteilt wurde und jeder fünfte Angeklagte trotz Freispruch schuldig ist! Da beide Fehler von einander abhängen, können nicht beide gleichzeitig minimiert werden. Mit sinkendem nimmt automatisch zu.
Die Durchführung eines statistischen Tests…
…geschieht immer in drei Schritten:
Schritt 1: Formulierung der Hypothesen
Sowohl die Nullhypothese H0, als auch die Alternativhypothese H1 werden formuliert. Dieser Formulierung kommt bei statistischen Tests eine zentrale Bedeutung zu, wie aus dem Beispiel des Gerichtsprozesses deutlich wird. Hier sollte immer größte Sorgfalt herrschen und die Hypothesen schriftlich festgehalten werden.
Schritt 2: Berechnung einer Prüfgröße
Abhängig vom statistischen Test wird eine Prüfgröße berechnet, welche im dritten Schritt mit einem Grenzwert verglichen wird. Für manche Tests lässt sich auch ein p-Wert berechnen, der direkt mit der Signifikanz α verglichen werden kann.
Schritt 3: Testentscheidung
Im dritten Schritt wird die Testentscheidung durch den Vergleich der Prüfgröße mit einem Grenzwert oder durch den Vergleich des p-Wertes mit der Signifikanz α getroffen. Es wird also entweder die Nullhypthese beibehalten oder verworfen.
Ein Beispiel: Vergleich zweier Stichproben (Wöhlerversuche) mit dem t-Test
In unserem Beispiel haben wir zwei Wöhlerversuche des gleichen Werkstoffes aber einer unterschiedlichen Charge auf demselben Lastniveau durchgeführt. Die ermittelten Lebensdauern N zeigt folgende Tabelle. Darin sind die experimentell ermittelten Lebensdauern N, deren logarithmierte Werte Log10(N) und für jede Stichprobe der Mittelwert x1 und x2 sowie die Standardabweichung s1 und s1 der logarithmierten Werte dargestellt. Es wird der logarithmus verwendet, da sich die logarithmierten Zyklenzahlen normalverteilen (siehe dieser Artikel Link).
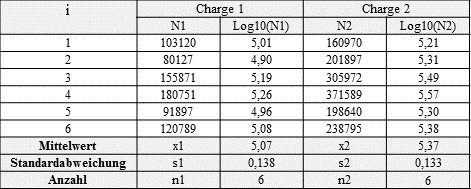
Ein Beispiel für einen statistschen t-Test mit Wöhlerlinien
Die Frage ist: unterscheiden sich die beiden Chargen im Mittel voneinander, wenn ein Signifikanzniveau von α = 5% angenommen wird?
Zur Beantwortung der Frage gehen wir nach den oben beschriebenen drei Schritten vor.
Schritt 1: Formulierung der Hypothesen
Für unser Beispiel lautet die Nullhypothese H0:
Die Mittelwerte beider Chargen sind gleich (x1=x2, oder x1-x2=0).
Die Alternativhypothese H1 lautet:
Die Mittelwerte beider Chargen unterscheiden sich (x1 ≠ x2).
Schritt 2: Berechnung der Prüfgröße des t-Tests
Für unser Beispiel wollen wir Unterscheide bezüglich des Mittelwertes testen und nehmen an, dass die Daten normalverteilt sind (wenn die Lebensdauern logarithmiert werden). Da zwei Stichproben (oder Gruppen) untersucht werden sollen, gilt also der t-Test.
Dieser Test wurde im Jahr 1908 unter dem Pseudonym Student vorgestellt. Mit ihm lassen sich Mittelwertunterschiede schnell und einfach identifizieren. Hinter dem Pseudonym steckt William Sealy Gosset, der bei der Guinness-Brauerei arbeitete (was ihn schon sympatisch macht;)) und den t-Test entwickelte um die Bier-Qualität zu überwachen. Da seitens des Unternehmens das veröffentlichen von Ergebnissen verboten war, publizierte er unter dem Pseudonym Student. Seine Herausforderung lag darin, dass er die Bierqualität erhöhen sollte, die auf Grund schlechter Chargen litt. Es galt umfangreiche Versuche zu vermeiden, bei denen das Bier anschließend weggeschüttet werden musste. Aus diesen Gründen (geringe Stichprobengröße und unbekannte Grundgesamtheit) entwickelte er den t-Test als statistisches Prüfverfahren.
Für die Durchführung des Tests wird ein Prüfwert (t-Wert t) für die Stichproben berechnet. Beim Einstichproben t-Test ist der t-Wert ist die Differenz der Mittelwerte der Stichproben bezogen auf den Standardfehler. Dieser t-Wert ist nicht mehr normalverteilt, sondern t-verteilt. Wobei die t-Verteilung der Normalverteilung ähnelt. Mit Hilfe der t-Verteilung lässt sich also berechnen, wie wahrscheinlich eine bestimmte Differenz des Mittelwertes der Stichprobe zum Mittelwert der Grundgesamtheit ist. Dabei ist die t-Verteilung nur abhängig vom Freiheitsgrad .
Der t-Wert berechnet sich für den Zweistichproben t-Test nach folgender Gleichung
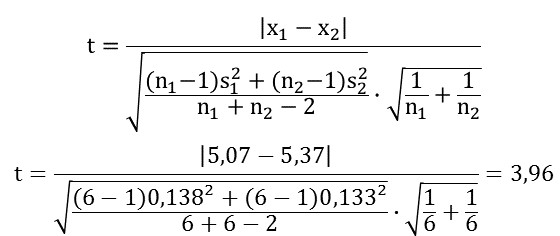
Es ist
t der t-Wert
x der Mittelwert der jeweiligen Stichprobe,
s die Standardabweichung der jeweiligen Stichprobe
n der jeweilige Stichprobenumfang.
Der Freiheitsgrad υ ist
υ = n1 + n2 - 2 = 6 + 6 - 2 = 10
Die einzuhaltenden Randbedingungen sind:
- Die Stichproben sind zufällig und repräsentativ
- Die Standardabweichung und die Varianz der Grundgesamtheit sind unbekannt.
- Beide Varianzen sind gleich.
- Die Grundgesamtheit der Daten ist normalverteilt oder der Stichprobenumfang beträgt mindestens 30 Werte.
Schritt 3: Testentscheidung des t-Tests
Folgende Abbildung zeigt schematisch die t-Verteilung. Es werden drei Fragestellungen unterschieden.
- Der linksseitige Test
- Der rechtsseitige Test und
- Der zweiseitige Test.
Abhängig von dieser Fragestellung wird die Testentscheidung gefällt. Betrachten wir zunächst den linksseitigen Test (Fall 1). Liegt der t-Wert unterhalb (links) eines Grenzwertes , wird angenommen, dass die Unterschiede nicht mehr zufällig, sondern mit der Wahrscheinlichkeit α statistisch signifikant sind. Es wird also die Nullhypothese H0 abgelehnt und die Alternativhypothese H1 akzeptiert.
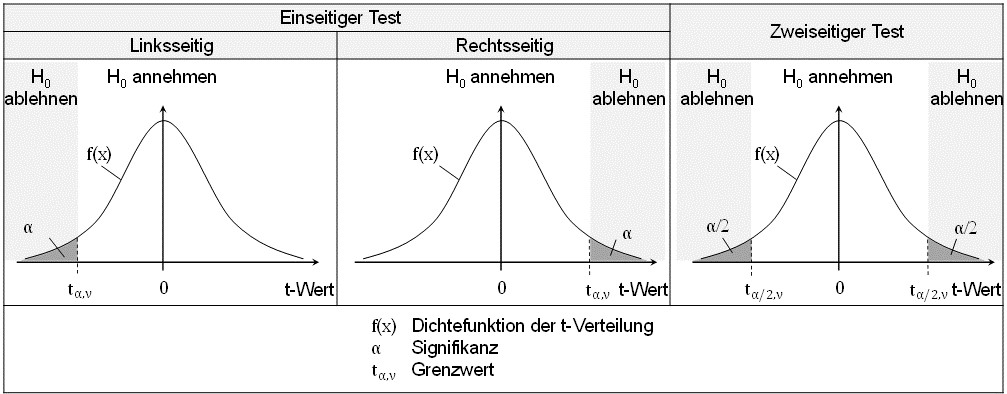
Erklärung der einseitigen und der zweiseitigen Fragestellung bei statistischen Tests am Beispiel des t-Tests
Für den rechtsseitigen Test (Fall 2) wird die Nullhypothese H0 abgelehnt, wenn der t-Wert oberhalb (rechts) eines Grenzwertes tα,υ liegt.
Bei der zweiseitigen Fragestellung (Fall 3) wird die Nullhypothese H0 abgelehnt, wenn der t-Wert oberhalb oder unterhalb eines Grenzwertes tα,υ liegt.
Der Grenzwert tα,υ ist abhängig vom Signifikanzniveau α und dem Freiheitsgrad υ (abhängig von der Art des t-Testes). Der Grenzwert kann z. B. folgender Tabelle entnommen werden. Hier sind nur positive Werte angegeben. Für den linksseitigen t-Test gilt also der negative Wert.
Zusammenfassend gilt für die Testentscheidung auf Basis des t-Wertes:
Die Nullhypothese H0 wird akzeptiert, wenn
t ≥ -tα,υ (linksseitige Fragestellung, Fall 1)
t ≤ tα,υ (rechtsseitige Fragestellung, Fall 2)
t ≤ tα,υ (zweiseitige Fragestellung, Fall3)
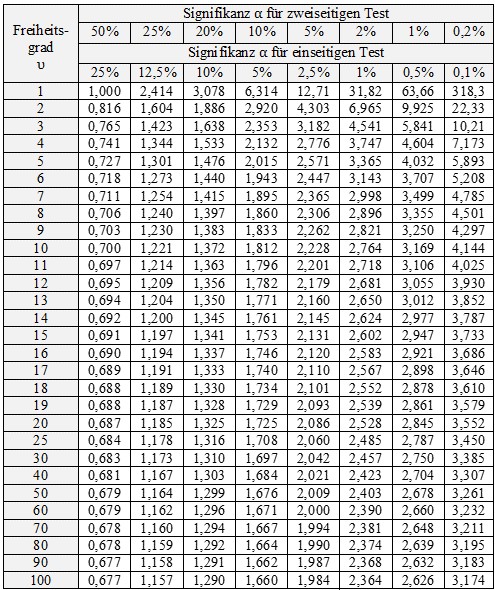
Tabelle mit Grenzwerten des t-Tests
Für unser Beispiel gilt die zweiseitige Fragestellung, da x1 > x2 oder x1 < x2 sein kann. Damit berechnet sich der Freiheitsgrad nach:
υ = n1 + n2 - 2 = 6 + 6 - 2 = 10
Mit dem Signifikanzniveau von α=5% wird als Grenzwert aus Tabelle abgelesen (zweiseitige Fragestellung):
tα=5%,υ=10 = 2,228
Da
t=3,96 > tα=5%,υ=10 =2,228
wird die Nullhypothese abgelehnt und akzeptiert, dass sich beide Chargen signifikant voneinander unterscheiden.
Zu beachten ist, dass mit steigender Stichprobenzahl (größerer Freiheitsgrad) die Prüfgröße abnimmt. Dadurch können kleiner Unterschiede festgestellt werden. Allerdings ist ab einem Freiheitsgrad von 20 keine signifikante Abnahme mehr feststellbar.
Wichtig ist noch zu erwähnen, dass dies kein Beweis ist! Es bleibt noch eine Unsicherheit vorhanden. Auf über die Ursachen des Unterschiedes gibt die Statistik keinen Aufschluss. Dies muss eine werkstoffmechanische Untersuchung klären.
Und wie gewohnt gibt es auch hier noch einen HEISSEN TIPP:
Dieser Test kann auch ganz einfach online z.B. unter http://signifikanzrechner.de/student-t-test/ durchgeführt werden.
Auf den Punkt:
Die Statistik und die statistischen Tests
- helfen, Aussagen auch für streuende Daten zu treffen.
- liefern keine absoluten Aussagen oder Beweise
- bieten Entscheidungsmöglichkeiten, allerdings sind die Ergebnisse durch werkstoffmechanische Untersuchungen zu untermauern
- mit steigender Stichprobenzahl (größerer Freiheitsgrad) die Prüfgröße abnimmt
Um es in einem kurzen Satz zu formulieren: Statistische Tests oder Methoden machen das Bauchgefühl greifbar und liefern bei unsicherer Datenlage Entscheidungsvorlagen.
