Der schmale Grat zwischen Dateninterpretation und -Manipulation

Als Ingenieure vor allem aus dem Umfeld der Entwicklung, Fertigung und Erprobung haben wir es mit streuuenden Daten zu tun. Diese gilt es zu interpretieren und daraus Schlüsse zu ziehen und Entscheidungen zu treffen. Allerdings: Daten können immer unterschiedlich interpretiert werden! Ich zeige Ihnen die Grundalgen auf, Daten fachmännisch und nicht manipulativ zu interpretieren.

Daten können immer unterschiedlich interpretiert werden, z. B. abhängig von der Person oder dem Interesse desjenigen, der interpretiert. Dazu ein kleines Beispiel zur Illustration.

Der sicherste Beruf der Welt ist Präsident der Vereinigten Staaten von Amerika. In den 225 Jahren, die es diesen Beruf gibt, sind nur vier Berufstätige durch einen "Arbeitsunfall" ums Leben gekommen. Der durchschnittliche Abstand zwischen zwei tödlichen Unfällen liegt bei 56 Jahre.

Der gefährlichste Beruf der Welt ist Präsident der Vereinigten Staaten von Amerika. Von 43 Berufstätigen kamen fast 10% - also jeder zehnte - durch einen "Arbeitsunfall" ums Leben. Diese Quote erreichen noch nicht einmal Fischer, Bergleute oder Soldaten.

Ist die Absicht hinter der Dateninterpretation positiv, dann spricht man von einer fachmännischen Interpretation. Ist die Intention dagegen negativ, spricht man von Manipulation. Um im Ingenieursalltag zu fachmännischen Interpretationen zu kommen, ist es wichtig, die statistischen Methoden richtig anzuwenden.

Auf Grund der Dateninterpretation werden Entscheidungen getroffen. Z.B. ist Material A besser als Material B, oder hatte die Wärmebehandlung einen Einfluss oder nicht. Dazu werden statistische Tests angewandt, deren Basis immer eine Hypothesenformulierung ist. Um hier fachmännisch Aussagen treffen zu können werden dazu die Grundlagen beschrieben.

Grundlagen statistischer Tests, oder: wie sicher ist meine Aussage?

Am Beispiel von Spam Mails soll der statistische Test anschaulich erklärt werden. Spam Mails sind ein großes Problem geworden, dem man versucht mit Hilfe von Spamfiltern entgegenzuwirken. Wie funktioniert ein solcher Filter?

Jede eingehende Email wird daraufhin getestet, ob sie eine Spam Mail ist oder nicht. Diese Aussage ist nicht eindeutig möglich, also fehlerbehaftet. Damit kann dies als statistisches Problem angesehen werden. Es werden zwei Hypothesen gebildet, die statistisch überprüft werden sollen. Deswegen spricht man statistisch von einem Hypothesentest. Dazu lauten die beiden Hypothesen:

• Die eingehende Mail ist eine Spam Mail
  Diese Hypothese wird als Nullhypothese H0 bezeichnet. Die Nullhypothese ist somit: Die eingehende Mail ist eine Spam Mail.
• Die eingehende Mail ist keine Spam Mail
  diese Hypothese wird als Alternativhypothese bezeichnet H1. Die Alternativhypothese ist immer das Gegenteil der Nullhypthese. Sie wird wie folgt formuliert: die eingehende Mail ist keine Spam Mail.

Leider ist es nicht möglich, eine hundertprozentige Aussage zu treffen. Es ist also durchaus möglich, dass eine Mail, fälschlicherweise als Spam deklariert und damit gelöscht wurde. Genauso ist es möglich, dass eine Spam Mail nicht als solche erkannt wurde und bei uns im Postfach landet.

Für unseren Spamfilter sind damit vier Szenarien möglich (siehe auch folgende Tabelle).

1. Angenommen, eine eingehende Mail ist eine Spam Mail (die Nullhypothese H0 ist wahr) und
   a) die Email wird vom Spamfilter als Spam Mail eingestuft, dann wurde die richtige Entscheidung getroffen.
   b) die Email wird vom Spamfilter nicht als Spam erkannt, dann ist eine falsche Entscheidung getroffen worden. Dieser Fehler wird als Fehler zweiter Art, oder falsch negatives Ergebnis bezeichnet (in der Realität liegt dieser Fehler bei guten Spam Filtern bei etwa β=1..10%).
2. Angenommen, eine eingehende Mail ist eine normale Email (die Alternativhypothese H1 ist wahr) und
   a) die Email wird vom Spamfilter als normale Email eingestuft, dann wurde die richtige Entscheidung getroffen.
   b) die Email wird vom Spamfilter nicht als normale Email erkannt, dann ist eine falsche Entscheidung getroffen worden. Dieser Fehler wird als Fehler erster Art, oder als falsch positives Ergebnis bezeichnet (in der Realität liegt dieser Fehler bei guten Spam Filtern bei etwa α<<1%).

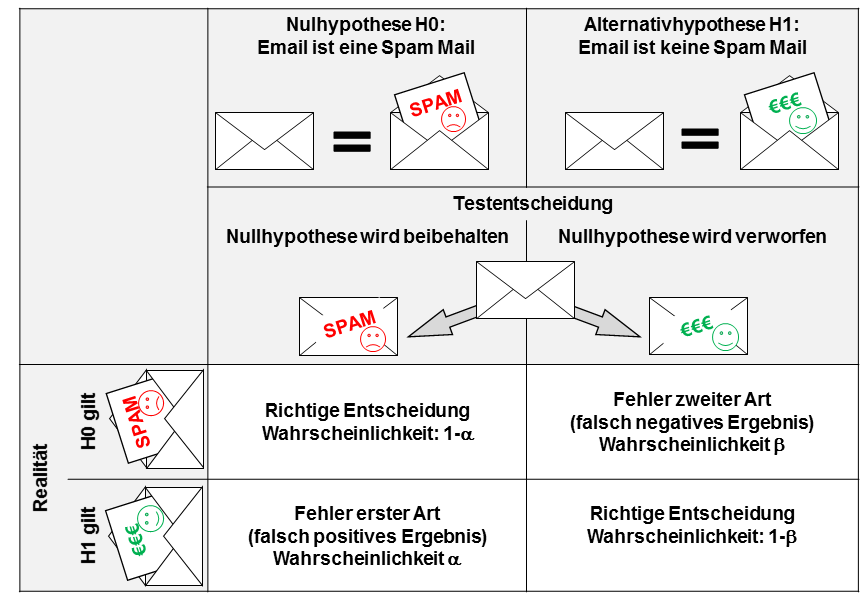
Obige Tabelle fasst dies noch einmal grafisch zusammen. Daraus wird deutlich, dass jede statistische Aussage fehlerbehaftet ist. Eine absolut sichere Aussage ist somit nicht möglich. Schauen wir dazu wieder auf das Beispiel des Spamfilters. Eine Forderung, niemals wieder eine Spam Mail zu erhalten ist gleichbedeutend mit der Forderung, dass der Fehler erster Art bei α = 0% liegt. In der Praxis bedeutet dies: Jede eingehende Email wird als Spam Mail eingestuft. Wir erhalten also überhaupt keine Email mehr (was für ein schönes Leben;)). Es steigt damit gleichzeitig das Risiko des Fehlers zweiter Art ins Unendliche  (eine Email, die keine Spam Mail ist wird als Spam identifiziert). Der Fehler erster und zweiter Art hängen also voneinander ab.

Es ist in der Statistik einfacher einen Fehler erster Art zu minimieren, als einen Fehler zweiter Art. Im Falle des Spam Filters ist es in der Realität möglich, den Fehler erster Art auf nahezu null zu bringen (α<<1%). Für den Fehler zweiter Art ist dies nicht möglich. In der Realität liegt dieser bei Spamfiltern bei ß=1..10%.

Nullhypothese und Alternativhypothese:

Für die Testplanung ist es deswegen wichtig, dem kritischeren Ergebnis den Fehler erster Art zuzuweisen. Bei dem Spam Filter ist es kritischer, dass eine an uns gerichtete Email fälschlicherweise als Spam bezeichnet und gelöscht wird, als der gegenteilige Fall (eine Spam Mail wird versehentlich nicht als solche erkannt).

Aus dieser Überlegung folgt zu einem Entscheidungsschema in drei Schritten zur Formulierung der Nullhypothese und der Alternativhypothese (Quelle: Link):

Schritt 1: Ist bekannt, ob ein Zusammenhang gezeigt oder widerlegt werden soll?

Falls ja: Formulierung der Nullhypothese so, dass der Zusammenhang widerlegt wird, bzw. Formulierung der Alternativhypothese so, dass der Zusammenhang gezeigt wird.

Falls nein: Schritt zwei.

Schritt 2: Sind die Konsequenzen der Fehler bekannt?

Falls ja: Formulierung der Hypothesen in der Art, dass der schwerwiegendste Fehler zum Fehler erster Art wird (vgl. den Spam Filter). Der Hintergrund ist, dass die Wahrscheinlichkeit des Fehlers erster Art  festgelegt werden kann.

Falls nein: Schritt drei.

Schritt 3: Ist bekannt, zu welcher Interessensgruppe der Prüfer gehört?

Falls ja: Formulierung der Alternativhypothese in der Art, dass diese durch den Prüfer nachgewiesen werden muss.

Falls nein: eine eindeutige Hypothesenformulierung ist nicht möglich.

Der Hintergrund liegt darin, dass es Ziel eines statistischen Tests ist, die Nullhypothese zu verwerfen. Dies ist vergleichsweise gut möglich, da der Fehler erster Art der hier begangen wird „eingestellt“ werden kann, also praktisch beeinflusst werden kann. Dies ist für den Fehler zweiter Art nicht möglich.

Ganz allgemein wird noch zwischen einseitigen und zweiseitigen Test unterscheiden. Am Beispiel von Unterscheiden zwischen zwei Mittelwerten x1 und x2 wird dies gezeigt. Zielt die Nullhypothese auf Gleichheit, dann gilt:

H0: x1 = X2

Für die Alternativhypothese gibt es jetzt mehrere Möglichkeiten, abhängig davon, was gezeigt werden soll:

H1: x1 < x2 (einseitiger Test nach unten oder linksseitger Test)
H1: x1 > x2 (einseitiger Test nach unten oder rechtsseitger Test)
H1: x1 ≠ x2 (beidseitiger Test)

Statistische Tests können auf Mittelwerte, Streuungen oder Verteilungen zielen. Die Formulierung der beiden Hypothesen hängt von dem Ziel des Testes ab. Dazu das Beispiel Klimawandel: Die Regierung möchte beweisen, dass es ihn nicht gibt, Umweltschützer möchten beweisen, dass es ihn gibt. Beide Gruppen werden also unterschiedliche Hypothesen formulieren. Warum das so ist und auch warum die Hypothesenformulierung so wichtig ist wird deutlich, wenn beide Fehler (Fehler erster und zweiter Art) näher betrachtet werden.

Fehler erster Art / Signifikanz

Die Wahrscheinlichkeit α einen Fehler erster Art zu begehen nennt man auch Signifikanz. Der Grenzwert, ab dem von einem statistisch signifikanten Ergebnis gesprochen wird ist das Signifikanzniveau. Typischerweise wird in der Technik das Signifikanzniveau wie folgt gewählt:

α = 5 %

Damit wird eine Fehlerhäufigkeit (Fehler erster Art) von bis zu 5% akzeptiert! Es handelt sich hierbei um eine pure Definition. Ist dies nicht ausreichend (siehe Ausführungen weiter vorne), muss das Signifikanzniveau a angepasst werden.

Dem Signifikanzniveau wird der p-Wert gegenübergestellt. Der p-Wert wird unter der Annahme berechnet, dass die Nullhypothese stimmt. Je größer der p-Wert, umso eher spricht das Ergebnis für die Nullhypothese. Ist der p-Wert kleiner als das Signifikanzniveau a, wird die Nullypothese verworfen, andernfalls wird sie akzeptiert:

H0: wird verworfen, wenn p ≤ α
H0: wird akzeptiert, wenn p > α.

Was ist der p-Wert in der Statistik anschaulich?

Angenommen, Sie spielen gerne Roulette im Casino. Dabei setzen Sie immer auf Rot. Theoretisch ist die Wahrscheinlichkeit genau bei 50% (wir vernachlässigen hier großzügig die Null), dass die Kugel bei einer roten oder schwarzen Zahl landet. Es fällt die Kugel nun zum dritten Mal nacheinander auf Rot. Die Frage ist, wann würden Sie annehmen, dass dies kein Zufall mehr ist, Sie also betrogen werden?

Als Nullhypothese formulieren wir für dieses Beispiel, dass beide Farben (rot und schwarz) sind gleich wahrscheinlich sind

H0: p(rot) = p(schwarz)

Die Alternativhypothese lautet:

H0: p(rot) ≠ p(schwarz)

In der Statistik wird der p-Wert unter der Annahme berechnet, dass die Nullhypothese stimmt.

Betrachten wir die Wahrscheinlichkeit für dieses Ereignis. Die Wahrscheinlichkeit eines nicht gezinkten Roulettisches für das Ergebnis „Rot“ liegt bei 50 %. Demnach liegt die Wahrscheinlichkeit für drei aufeinanderfolgende Ergebnisse „Rot“ bei 0,5*0,5*0,5 = 0,5³ = 0,125 =12,5% (In Realität gibt es 37 Möglichkeiten für die Kugel. Davon sind 18 Rot, 18 schwarz und 1 ohne Farbe, nämlich die Null. Damit ist Wahrscheinlichkeit für Rot bei p(rot)=18/37=0,49=49%). Das bedeutet, dass dieses Ereignis mit einer Wahrscheinlichkeit von 12,5% möglich ist. Nach den Kriterien der Wissenschaft würden wir also noch annehmen, dass das Ergebnis zufällig und der Roulettisch nicht gezinkt ist, da das Signifikanzniveau von α = 5%  noch nicht unterschritten ist. Erst nachdem die Kugel zum fünften Mal nacheinander auf Rot gefallen ist, werden wir hellhörig! Die Wahrscheinlichkeit für dieses Ereignis liegt dann mit 0,5*0,5*0,5*0,5*0,5=0,031=3,1% unter dem Signifikanzniveau von α = 5%. Bewiesen ist unsere Aussage damit nicht! Wir gehen nur mit einer gewissen Wahrscheinlichkeit davon aus, dass der Würfeltisch gezinkt ist. Es liegt noch immer die Irrtumswahrscheinlichkeit bei 3%, obwohl das Ergebnis als statistisch signifikant angesehen wird! Würden Sie auf dieser Basis das Casino verklagen?

Da die Anschuldigung schwerwiegend ist, wird das Signifikanzniveau deutlich auf α = 1% abgesnkt. In diesem Fall unterstellen wir erst nach dem siebten Rot in Folge einen Betrug (0,5⁷=0,0078=0,78%). Es zeigt sich, dass die Aussagegenauigkeit stark von der Stichprobe abhängt. Im vorliegenden Beispiel mussten sieben „Versuche“ gemacht werden, um eine Signifikanz von 1% nachzuweisen. Bei einer Signifikanz von 5% waren es dagegen nur fünf „Versuche“. Aus Sicht eines Ingenieurs bedeutet dies, dass die Anzahl an Versuchen zur Überprüfung einer Hypothese beachtet werden muss. Dies ist aus Zeit- und Kostengründen wichtig.

Wird die Nullhypothese verworfen, liefert uns der statistische Test niemals die Ursache! In diesem Beispiel könnte es sein, dass absichtlich manipuliert wurde, durch Verschleiß des Tisches die Ursache zufällig hervorgerufen wurde oder das Ergebnis schlicht zufällig ist. Ein statistisch signifikantes Ergebnis muss deswegen mit dem Ingenieurssachverstand auf Plausibilität und Ursache überprüft werden. Erst wenn die technische Ursache gefunden ist, können wir uns der Aussage sicher sein.

Fehler zweiter Art

Im Gegensatz zum Fehler erster Art, kann die Wahrscheinlichkeit β eines Fehlers zweiter Art im Allgemeinen nicht berechnet werden. Der Fehler zweiter Art besagt, dass die signifikante Aussage: der Roulettisch liefert unterschiedliche Wahrscheinlichkeiten für rot und schwarz, falsch ist. In Wahrheit sind beide Wahrscheinlichkeiten gleich und die festgestellten Unterscheide zufällig. Die Nullypothese wurde fälschlicherweise abgelehnt, das Ergebnis ist falsch negativ.

Üblich in der Statistik ist die Vorgabe, dass

β < 20%

liegen soll. Der Fehler zweiter Art β hängt neben der Stichprobengröße  auch vom Fehler erster Art a ab. Je kleiner a gewählt wird, umso größer wird β (vgl. das Beispiel des Spam Filters). Es muss also ein Kompromiss aus beiden Fehlern gefunden werden. Üblich ist:

α = 5%
β = 20%.

Ein Beispiel aus der Technik stellt den Umgang mit der Hypthesenformulierung dar:

Eine typische technische Fragestellung dazu ist die Qualifizierung eines neuen Zulieferers für einen Werkstoff. Die Freigabe soll in einem ersten Schritt anhand der Zugfestigkeit Rm erfolgen. Dazu werden die Zugfestigkeiten von jeweils zehn Proben des neuen Zulieferers gemessen und der Mittelwert Rm1 gebildet. Dieser wird mit dem Mittelwert  von zehn gemessenen Zugfestigkeiten des alten Zulieferers verglichen (Rm2). Die Frage ist: Darf angenommen werden, dass diese beiden Mittelwerte gleich sind? Kann also der neue Zulieferer zugelassen werden?

Bei der Formulierung der Nullhypothese wird nach dem obigen Schema vorgegangen. Es ist nicht bekannt, ob gezeigt werden soll, dass beide Zulieferer Werkstoffe mit derselben Zugfestigkeit liefern oder nicht (Schritt 1). Betrachten wir also das Risiko (Schritt 2). Es ist kritischer, wenn der neue Zulieferer zugelassen wird, obwohl dessen Werkstoffe eine geringere Zugfestigkeit aufweisen als gefordert. Demnach muss dies der Fehler erster Art sein. Dies ist der Fall, wenn der Test fälschlicherweise aussagt, dass  (vgl. auch Tabelle 4). Damit gilt für die Nullhypothese H0:

H0: Rm1 ≥ Rm2

und für die Alternativhypothese H1:

H1: Rm1<Rm2

Die Wahrscheinlichkeit, dass die Alternativhypothese gilt, obwohl auf grund des statistischen Tests angenommen werden kann, dass Rm1 ≥ Rm2, liegt bei der Wahrscheinlichkeit α. Diese kann frei gewählt werden. Absolute Sicherheit gibt es jedoch nicht!

Für uns Ingenieure bedeutet dies: Es können mit der Statistik keine Beweise geführt werden (eine absolute Sicherheit gibt es in der Statistik nicht)! Allein die Aussage ist möglich, dass eine Aussage mit einer gewissen Wahrscheinlichkeit stimmt oder abgelehnt werden muss. Jede statistische Aussage beinhaltet damit immer das Risiko sich zu irren! Deswegen ist es unbedingt notwendig, die Ergebnisse auf Basis des klassischen Ingenieurwissens immer wieder! kritisch zu hinterfragen.

Auf dem Punkt

• Nutzen Sie die Methoden der Statistik richtig, um nicht den Anschein der Manipulation zu erwecken. Dazu ist die Formulierung der Nullhypothese extrem wichtig.
• Wähle die Nullhypothese so, dass der schlimmere Fehler, mit dem Fehler erster Art zusammenfällt, da dieser beliebig reduziert werden kann.
• Der Fehler zweiter Art kann nicht direkt beeinfluss werden.
• Typische Größen für den Fehler erster Art sind α = 5%
• Typische Größen für den Fehler zweiter Art sind β = 20%
• Ein Statistischer Test liefert niemals Beweise, maximal Indizien! Die Ursachen müssen durch Ingenieurssachverstand gefunden werden.
• Eine absolute Sicherheit gibt es nicht!

In unserem Buch Statistik der Betriebsfestigkeit erfahren Sie, wie Sie die wichtigsten statistischen Methoden der Betriebsfestigkeit anwenden können:

Informieren