Systemzuverlässigkeiten beliebiger Bauteile endlich einfach berechnen
 Um Produkte sicher auf deren geforderte Zuverlässigkeit auslegen zu können, muss deren Systemzuverlässigkeit berechnet werden. Diese setzt sich aus den Einzelzuverlässigkeiten der Komponenten zusammen. In diesem Artikel erfahren Sie, wie Sie Systemzuverlässigkeiten schnell und einfach berechnen können um größere Fehler zu vermeiden.
Um Produkte sicher auf deren geforderte Zuverlässigkeit auslegen zu können, muss deren Systemzuverlässigkeit berechnet werden. Diese setzt sich aus den Einzelzuverlässigkeiten der Komponenten zusammen. In diesem Artikel erfahren Sie, wie Sie Systemzuverlässigkeiten schnell und einfach berechnen können um größere Fehler zu vermeiden.
In diesem Artikel lernen Sie,
- Was eine Systemzuverlässigkeit ist
- Wie Sie für Ihre Systeme die Systemzuverlässigkeit auf Basis der Einzelzuverlässigkeiten berechnen
- Welche Rolle dabei die FMEA spielt
- Praktische Tipps für die Anwendung im Alltag kennen
Inhalt
- Grundlagen
- Zu Schritt 1: Ermittlung aller potenzieller Fehler
- Zu Schritt 2: Zuweisung einer akzeptierten Ausfallwahrscheinlichkeit für jeden potenziellen Fehler
- Zu Schritt 3: Erarbeitung der Systemstruktur und Berechnung der Systemzuverlässigkeit für Reihenschaltungen
- Auf den Punkt
- Weiterführende Informationen
1 Grundlagen
Zuverlässigkeitsanforderungen können entweder für das Produkt, Komponenten oder auch einzelne Schadensmechanismen angegeben werden. Dabei sind zwei prinzipielle Fälle denkbar:
- Fall 1: Es wird eine Systemzuverlässigkeit gegeben. Gesucht ist die zulässige Einzelzuverlässigkeit der Komponenten bzw. Schadensmechanismen.
- Fall 2: Es sind die Einzelzuverlässigkeiten der Schadensmechanismen oder der Komponenten gegeben. Gesucht ist dann die Systemzuverlässigkeit.
Für den ersten Fall der Zuverlässigkeitsauslegung eines Produktes müssen diese Zuverlässigkeitsanforderungen des Produktes dann auf die Zuverlässigkeiten der Schadensmechanismen heruntergebrochen werden. Im zweiten Fall gilt es aus den Zuverlässigkeiten der Schadensmechanismen die Zuverlässigkeit des Produktes zu berechnen.
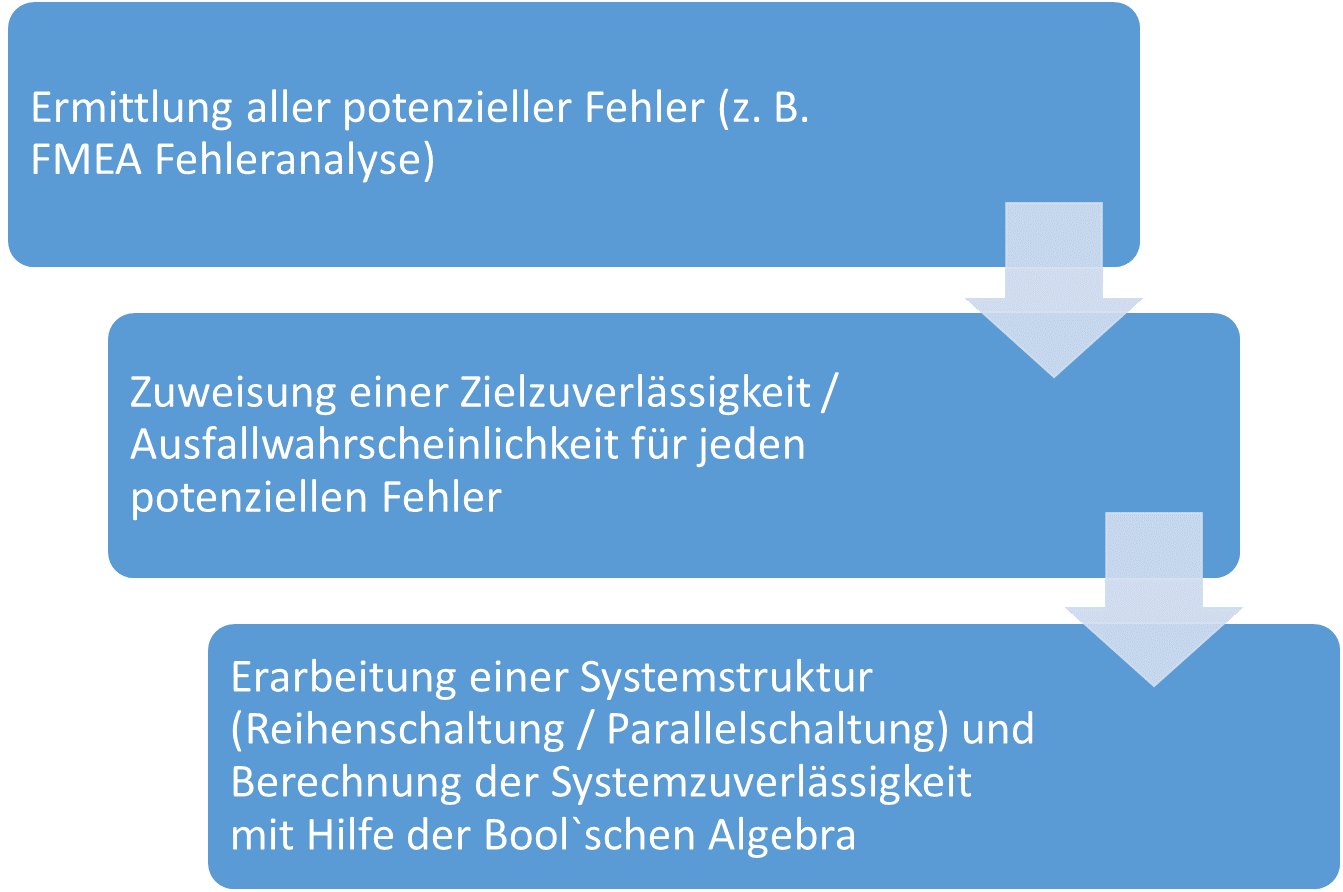
Die Berechnung der Systemzuverlässigkeit in drei einfachen Schritten
Zur Berechnung der Gesamtzuverlässigkeit geht man in drei Schritten vor (siehe obige Abbildung):
- Ermittlung aller potenzieller Fehler,
- Zuweisung einer Zuverlässigkeit oder einer akzeptierten Ausfallwahrscheinlichkeit für jeden potenziellen Fehler,
- Erarbeitung der Systemstruktur zur Verknüpfung der potenziellen Fehler und Berechnung der Systemzuverlässigkeit.
2 Zu Schritt 1: Ermittlung aller potenzieller Fehler:
Die vielleicht bequemste Art zu einer Liste mit allen potenziellen Fehlern zu gelangen ist die FMEA. Denn in Schritt 3 der FMEA hat man aus der Strukturanalyse und der Funktionsanalyse die Fehlfunktionsstruktur ermittelt. Damit liegen alle potenziellen Fehler bzw. Schadensmechanismen vor. Potenzielle Fehler sind alle Risiken, die zu einem Bauteilversagen und damit einer Kundenbeanstandung führen können.
In folgendem Link findet sich eine detaillierte Beschreibung für die Durchführung einer FMEA. Dies ist unser Buch zur Zuverlässigkeit.
3 Zu Schritt 2: Zuweisung einer akzeptierten Ausfallwahrscheinlichkeit für jeden potenziellen Fehler:
Eine Möglichkeit ist, dass man sich ebenfalls aus der FMEA bedient und die in Schritt 4 der FMEA ermittelten Ausfallwahrscheinlichkeiten verwendet. Siehe dazu folgende Tabelle nach „VDA, Qualitätskontrolle in der Automobilindustrie, Bd. 4 – Sicherung der Qualität vor Serieneinsatz, 2. Auflage, Frankfurt a.M. : VDA , 1986“.
| Auftretenswahrscheinlichkeit A | Allgemeine Bewertungskriterien für die Auftretenswahrscheinlichkeit A | Fehleranteil (Ausfallwahrscheinlichkeit) in ppm |
| sehr hoch 10 9 |
| sehr hoch 500.000 100.000 |
| hoch 8 7 |
| hoch 30.000 10.000 |
| mäßig 6 5 4 |
| mäßig 5.000 2.000 500 |
| gering 3 2 |
| gering 100 |
| sehr gering 1 |
| sehr gering 1 |
Falls dies keine Option ist, muss jedem potenziellen Fehler eine Ausfallwahrscheinlichkeit zugewiesen werden.
Bei der Festlegung der Ausfallwahrscheinlichkeit kann z.B. auf Erfahrungen, auf Vorgängerprodukte, Wettbewerberanalysen, Pannenstatistiken, Sicherheitsanforderungen, Fehlerauswirkungen, FMEA Bewertungen, … zurückgegriffen werden.
Da der Sicherheit von Produkten eine besondere Rolle zukommt, kann bei der Festlegung der zulässigen Ausfallwahrscheinlichkeiten auch eine Einteilung nach verschiedenen Ausfallarten helfen:
- nicht sicherheitskritische Ausfälle (z.B. Verschleiß, der erkannt und durch Wechsel des Bauteils behoben wird (z.B. Verschleiß Bremsscheiben im Fahrzeug) und
- sicherheitskritische (z.B. in der FMEA durch die Schwere = 9…10 gekennzeichnet, wenn etwa der Ausfall eine Gefahr für menschliches Leben darstellt).
3.1 Nicht sicherheitskritische Ausfälle
können auf Ausfallwahrscheinlichkeiten ausgelegt werden, die im Prozentbereich liegen. Dies hat den Vorteil, dass insbesondere verschleißrelevante Bauteile (Kugellager, Bremsscheiben, …) wirtschaftlich ausgelegt werden können. Typische Ausfallwahrscheinlichkeiten für Konstruktionen oder Baugruppen liegen bei z.B.
- Ausfallwahrscheinlichkeit PF = 1…10%
- Zuverlässigkeit R = 99…90%.
3.2 Sicherheitskritische Ausfälle
werden auf technische Null ausgelegt (beispielsweise 1ppm).
- Ausfallwahrscheinlichkeit PF ≈ 1 ppm.
Es gilt hier die Gefahr für Leib und Leben unbedingt so gering wie möglich zu halten. In keinem Fall dürfen für sicherheitskritische Ausfälle Wirtschaftlichkeitsrechnungen angestellt werden.
3.3 Ein besonders negatives Beispiel
dafür lieferte der Ford Pinto. Bei diesem Fahrzeugtyp konnte der Tank bei Auffahrunfällen einfach beschädigt werden und sich das Fahrzeug entzünden. Bei mehreren Unfällen kamen Menschen ums Leben. Ford war der Fehler bekannt. Es wurden jedoch die durch Klagen erwarteten Gerichtskosten geringer eingeschätzt, als die Kosten für die Änderung der Konstruktion. Weshalb die Konstruktionsänderungen verworfen wurden. In der Folge führte dies zu mehreren tödlichen Unfällen und Klagen gegenüber Ford. Die Klagen wurden zwar abgewiesen, jedoch war der daraus entstandene Imageschaden für Ford immens.
3.4 Praxistipp
Häufig sind die typischen Schwachstellen im Produkt oder auch die Komponenten mit den hohen Ausfallzahlen bekannt. Diesen werden dann die höheren Ausfallwahrscheinlichkeiten zugewiesen.
Die Erfahrung zeigt, dass z.B. typische PKW relativ hohe Ausfallwahrscheinlichkeiten bei Bremsbelägen, Lichtmaschinen, Anlassern, Elektronikkomponenten, … haben. Dagegen sind die Ausfallwahrscheinlichkeiten bei gebrochenen Gaspedalen, Motorhauben, abgefallenen Türen, … sehr gering. Diese Erfahrung kann man sich bei der Festlegung der Ausfallwahrscheinlichkeiten zunutze machen.
Erfahrene Konstrukteure haben dieses Wissen für Ihre Bauteile ebenfalls meist griffbereit!
Als Ergebnis liegt jetzt eine Liste mit allen potenziellen Fehlern und deren akzeptierter Ausfallwahrscheinlichkeit bzw. deren geforderter Zuverlässigkeit vor.
4 Zu Schritt 3: Erarbeitung der Systemstruktur und Berechnung der Systemzuverlässigkeit für Reihenschaltungen
Grundlegend kann man die Verschaltung von Ausfallmechanismen in drei Kategorieen einteilen:
- Die Reihenschaltung
- Die Parallelschaltung oder
- Eine Kombination aus Reihen-/ und Parallelschaltung.
Die Berechnung der Systemzuverlässigkeit erfolgt mit Hilfe der Boole’schen Systemtheorie durch die Bildung von Zuverlässigkeitsschaltbildern (siehe folgende drei Abschnitte und Abbildungen). Dabei müssen ein paar Annahmen eingehalten werden:
- Keine Wechselwirkungen: Die Komponenten beeinflussen sich nicht gegenseitig.
- Die Komponenten sind nicht reparierbar.
- Die Komponenten sind entweder ausgefallen oder funktionsfähig.
4.1 Die Reihenschaltung
Ziel der Systemstruktur ist es, festzustellen, wie sich die einzelnen Fehler auswirken. Üblicherweise geht man davon aus, dass ein Fehler immer zum Ausfall des Systems führt. In diesem Fall ist die Systemstruktur eine Reihenstruktur analog folgender Abbildung und vergleichbar mit dem einer Kette: Fällt ein Glied dieser Kette aus, dann ist die gesamte Kette ausgefallen.

Die Berechnung der Systemzuverlässigkeit bei einer Reihenschaltung
Im Fall der Reihenschaltung berechnet sich die Systemzuverlässigkeit RSystem aus dem Produkt der Einzelzuverlässigkeiten Ri:
- Systemzuverlässigkeit:
RSystem = Π Ri = R1 ∙ R2 ∙ … ∙ Rn. - Ausfallwahrscheinlichkeit des Systems:
PA,System = 1 – RSystem = 1- (R1 ∙ R2 ∙ … ∙ Rn).
Eine Reihenschaltung als Systemstruktur hat folgende spezifische Eigenschaften:
- Die Gesamtzuverlässigkeit immer kleiner als die kleinste Einzelzuverlässigkeit! Das bedeutet, dass die schwächste Komponente im System die Zuverlässigkeit des gesamten Systems dominiert!
- Deshalb ist es mit dieser Art von System enorm schwierig, sehr hohe Systemzuverlässigkeiten zu erreichen.
- Jede weitere Komponente führt zu einer geringeren Systemzuverlässigkeit.
- Gerade wenn die Anzahl an Komponenten und damit die Anzahl potenzieller Fehler zunimmt kann die Systemzuverlässigkeit trotz hoher Einzelzuverlässigkeit klein sein.
- Die Systemzuverlässigkeit berechnet sich aus dem Produkt der Einzelzuverlässigkeiten.
4.2 Die Parallelschaltung
Um hohe Systemzuverlässigkeiten sicherzustellen, kann man auf Redundanzen setzen wie folgende Abbildung zeigt. Werden mehrere Komponenten redundant eingesetzt, führt dies dazu, dass der Ausfall einer Komponente nicht zum Ausfall des Systems führt, sondern eine weitere Komponente „einspringt“.
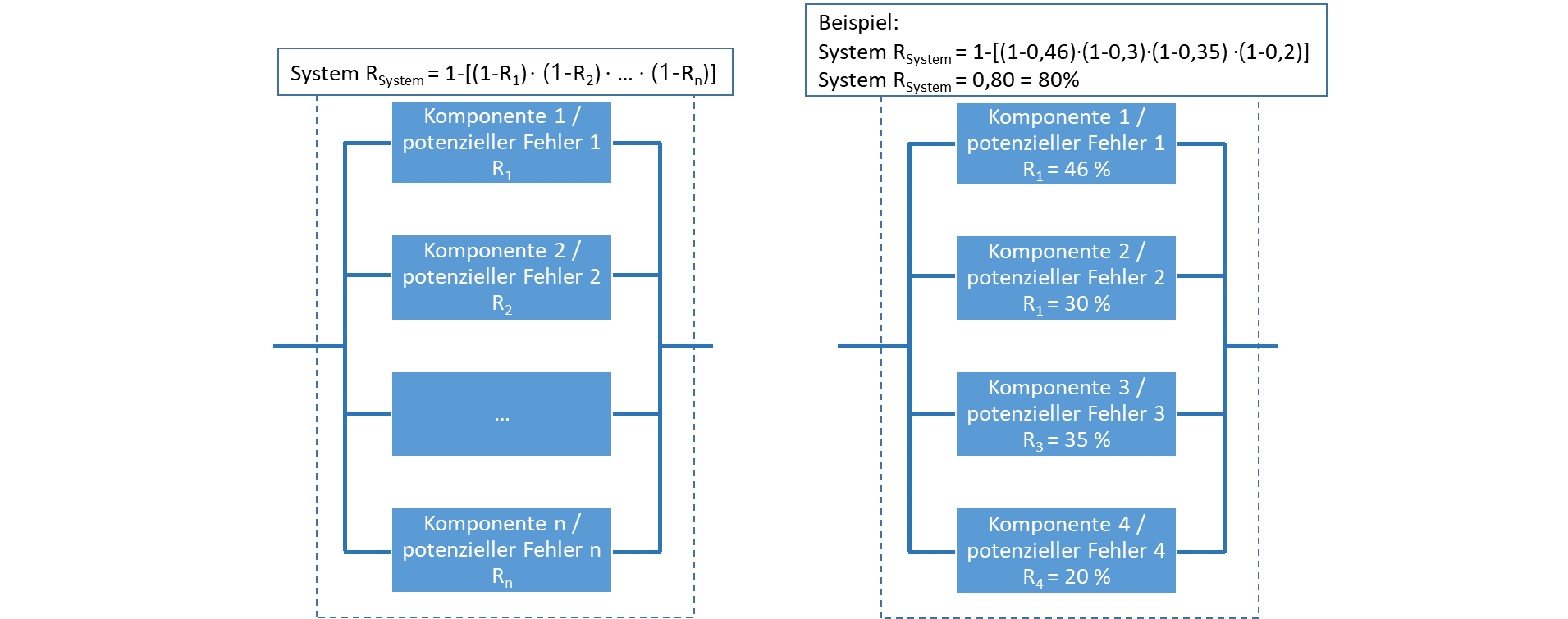
Die Berechnung der Systemzuverlässigkeit bei einer Parallelschaltung
Bei der Parallelschaltung berechnet sich die Systemzuverlässigkeit RSystem aus dem Produkt PA,System der Ausfallwahrscheinlichkeiten PAi der einzelnen Komponenten:
- Ausfallwahrscheinlichkeit des Systems:
PA,System = Π PA,i = PA,1 ∙ PA,2 ∙ … ∙ PA,n. - Systemzuverlässigkeit:
RSystem = 1 – PA,System = 1 – Π PA,i = 1 – [(1 – R1) ∙ (1 – R2) ∙…∙ (1 – Rn)]
Eine Parallelschaltung als Systemstruktur hat folgende spezifische Eigenschaften:
- Die Gesamtzuverlässigkeit ist immer größer als die größte Einzelzuverlässigkeit!
- Das bedeutet, dass trotz schwacher Einzel-Komponenten eine hohe Systemzuverlässigkeit erreicht werden kann!
- Jede weitere Komponente führt zu einer höheren Systemzuverlässigkeit.
4.3 Eine Kombination aus Reihen-/ und Parallelschaltung
Es sind auch beliebige Kombinationen aus Reihen und Parallelschaltungen denkbar. Um diese komplizierten Systeme zu bearbeiten, behilft man sich eines kleinen Tricks. Es werden Subsysteme gebildet und dann das komplizierte Gesamtsystem in eine einfache Reihenschaltung oder Parallelschaltung überführt. Das Vorgehen zeigt folgende Abbildung.
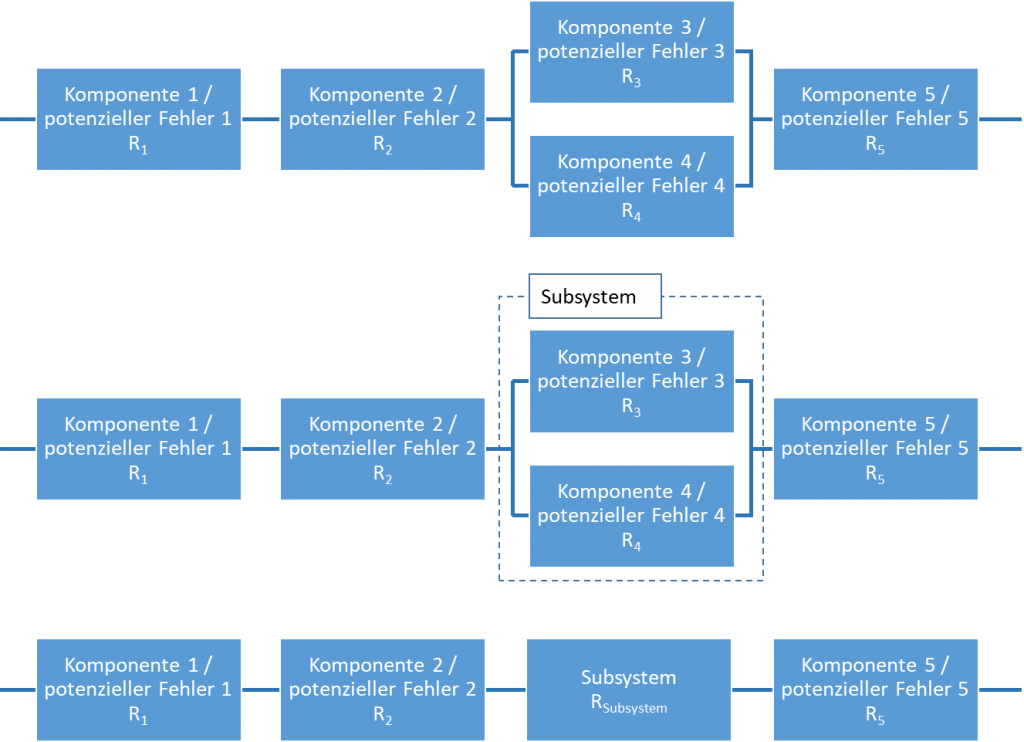
Umgang mit komplizierten Systemstrukturen mit einer Kombination aus Parallel- und Reihenstrukturen (oberes Bild). Vereinfacht durch Subsysteme (mittleres Bild) und überführt in einfache Strukturen (unteres Bild).
4.4 Berechnung der Systemzuverlässigkeit bei Annahme einer Weibullverteilung
Wenn die Zuverlässigkeit der Einzelkomponenten Ri durch z.B. eine Weibullverteilung beschrieben wird, dann lässt sich die Systemzuverlässigkeit im Falle der Reihenschaltung durch Einsetzen der Weibullverteilung in die Gleichung zur Berechnung der Systemzuverlässigkeit berechnen:
![]()
Im Falle der Parallelschaltung wird die Systemzuverlässigkeit wie folgt berechnet:
![]()
Neben der Systemzuverlässigkeit lässt sich mit den obigen Gleichungen auch die zu einer vorgegebenen Systemzuverlässigkeit RSystem(t) gehörende Systemlebensdauer t berechnen. Dies ist jedoch nur durch schrittweises Probieren möglich, d.h. es wird in obige Gleichungen eine geschätzt Systemlebensdauer tSchätzung eingesetzt und geschaut, welche Systemzuverlässigkeiten RSystem(tSchätzung) sich ergibt. Abhängig vom Ergebnis wird die geschätzte Systemlebensdauer solange geändert, bis die sich ergebende Systemzuverlässigkeit RSystem(tSchätzung) der gesuchten Systemzuverlässigkeit entspricht (RSystem(tSchätzung) = RSystem(t))
Mit Hilfe dieser Gleichungen lassen sich die Einzelzuverlässigkeiten und die Systemzuverlässigkeit auch in einem gemeinsamen Wahrscheinlichkeitsnetz darstellen (siehe folgende Abbildung). Ein großer Vorteil dieser Darstellung ist, dass auf einen Blick ersichtlich ist, welche Komponenten / potenziellen Fehler die Systemzuverlässigkeit dominieren und optimiert werden sollten.
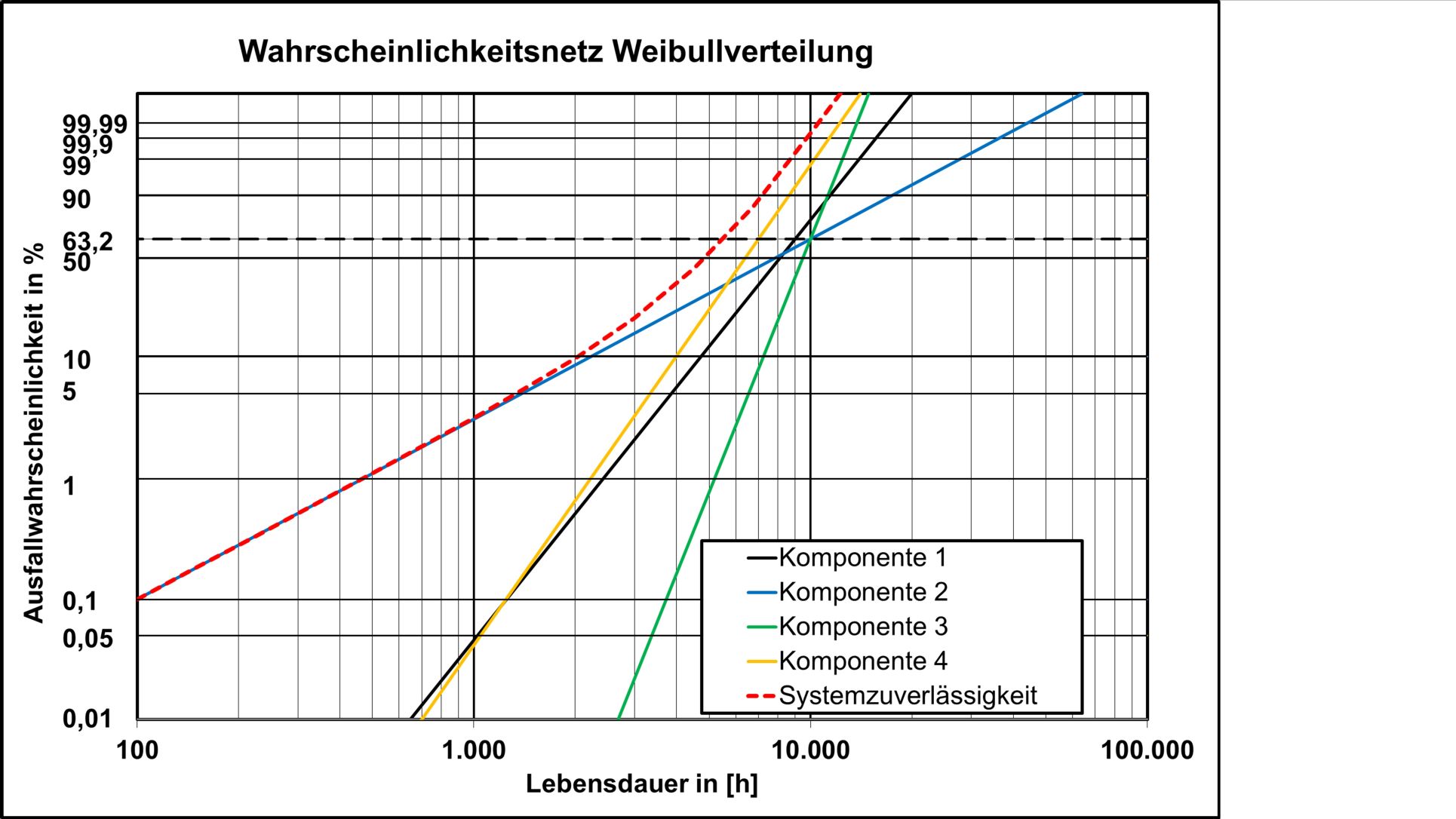
Darstellung der Systemzuverlässigkeit und der Einzelzuverässigkeit im Wahrscheinlichkeitsnetz
4.4.1 Praxistipp:
Bei der Darstellung der Systemzuverlässigkeit im Wahrscheinlichkeitsnetz nach obiger Abbildung werden üblicherweise nur die potenziellen Fehler / Komponenten mit den größten Ausfallwahrscheinlichkeiten (diejenigen, welche im Prozentbereich sind) dargestellt. Es lässt sich daraus dann sehr schön erkennen, welche Maßnahmen bei einer nicht ausreichenden Systemzuverlässigkeit helfen. Dies können z.B. sein:
- Reduzierung der Streuungen (falls möglich), wenn die Kurven sehr flach verlaufen,
- Steigerung der mittleren Zuverlässigkeit der kritischsten Komponente etwa durch den Einsatz einer robusteren Komponente,
- Einführung von Redundanzen.
Gleichzeitig können auch sehr zuverlässige Komponenten gezielt geschwächt werden, wenn deren Zuverlässigkeit sehr hoch ist. Dadurch lassen sich Kosten sparen.
5 Auf den Punkt
- Bei der Berechnung der Systemzuverlässigkeit wird in drei Schritten vorgegangen:
- Ermittlung aller potenzieller Fehler
- Zuweisung einer Zuverlässigkeit für jeden potenziellen Fehler (der Einzelzuverlässigkeit)
- Erarbeitung der Systemstruktur und Berechnung der Systemzuverlässigkeit
- Mit Hilfe der FMEA lassen sich sehr gut die Zielzuverlässigkeiten und die Einzelzuverlässigkeiten abschätzen, sowie die potenziellen Fehler finden.
- Die Systemzuverlässigkeit setzt sich aus den Einzelzuverlässigkeiten der Komponenten zusammen.
- Sie Einzelzuverlässigkeiten sind über die Systemstruktur miteinander verbunden
- Üblicherweise ist die Systemstruktur eine Reihenschaltung, in wenigen Fällen liegt eine Parallelschaltung vor. Selten eine komplexere Verschaltung.
- Bei der Reihenschaltung sinkt die Systemzuverlässigkeit mit einer steigenden Anzahl an Komponenten. Die Systemzuverlässigkeit ist immer kleiner als die kleinste Einzelzuverlässigkeit.
- Bei der Parallelschaltung steigt die Systemzuverlässigkeit mit der steigenden Anzahl an Komponenten. Die Systemzuverlässigkeit ist immer größer als die kleinste Einzelzuverlässigkeit.
- Wenn die Einzelzuverlässigkeiten über die Weibullverteilung beschrieben werden, dann kann die Systemzuverlässigkeit direkt aus den Einzelnen Weibullverteilungen berechnet werden.
- Eine Anschauliche Darstellung liefert das Wahrscheinlichkeitsnetz, in dem die Einzelzuverlässigkeiten und die Systemzuverlässigkeit gemeinsam dargestellt werden. Dadurch können sehr schön Schwachstellen und Potenziale identifiziert werden.
- Hier finden Sie ein Excel Tool für das Wahrscheinlichkeitsnetz.
Weiterführende Informationen
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren und Büchern. Außerdem können Sie den Inhalt des Artikels bewerten.
Bewerten Sie den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Technische Zuverlässigkeit - Bauteile robust auslegen und effizient erproben

Lernen Sie in dem
Seminar zur technischen Zuverlässigkeit
mittels qualitativer und quantitativer Methoden der Zuverlässigkeitsgestaltung und -validierung wie Sie Bauteile robust auslegen, um Ausfälle Ihrer Produkte zu vermeiden und wie Sie Bauteile effizient erproben um Risiken zu vermeiden und gleichzeitig Kosten bei der Erprobung zu sparen.
Sie lernen die
- Grundlagen der typischen Lebensdauerverteilungen wie, der Normalverteilung, Weibullverteilung, Exponentialverteilung sowie das Wahrscheinlichkeitsnetz den Vertrauensbereich kennen
- Versuche selbständig planen, auswerten und interpretieren
- Wahrscheinlichkeitsnetze inkl. Vertrauensbereiche erstellen und beurteilen
- das Festlegen des erforderlichen Stichprobenumfangs mittels Larson Nomogramm
- wichtige Lebensdauermodelle kennen: Arrhenius, Wöhlerlinien, Coffin-Manson, Norris-Landzberg.
- Regressionsmethoden anwenden und erfahren, wie Sie Versuchsergebnisse auf beliebige Ausfallwahrscheinlichkeiten umrechnen können
- die typischen Klassierungsmethoden Rainflow-Zählung und Momentanwertmethode anwenden
- wie unter Betrachtung bestimmungsgemäßer Gebrauch, Worst Case und Misuse Lastkollektive erstellt werden
- die lineare Schadensakkumulation als Methode zur Berechnung der Bauteillebensdauer anwenden
- Succes Run Erprobungen zu planen und auszuwerten
- wie Versuchszeiten gerafft werden können.
Außerdem werden
- alle Themen werden softwareneutral vorgestellt
- die Seminarinhalte durch ein umfangreiches Komplexbeispiel zusammengefasst.
Ziel dieses Seminars ist es, dass Sie danach Ihre bauteile robust auslegen und effizient erproben können.
Weiterführende Literatur

Produkte werden komplexer und Kundenansprüche bzgl. Nutzungsdauer, Qualität, Sicherheitserwartung und Kosten steigen. Man löst dieses Spannungsverhältnis verstärkt durch eine höhere Auslastung der Bauteile und effizientere Erprobungsmethoden. Hier helfen die Methoden der technischen Zuverlässigkeit, denn bei Kenntnis der Lasten, und der Werkstoffgrenzen können Bauteile höher ausgelastet und Erprobungskosten gespart werden.
Unser Buch
TECHNISCHE ZUVERLÄSSIGKEIT mit MINITAB® – Bauteile robust auslegen und effizient erproben
begleitet das Seminar und hilft Ihnen bei einem Einstieg oder der Vertiefung bei der Ableitung/Interpretation effizienter Erprobungen und dem Nachweis der Zuverlässigkeit Ihrer Produkte:
- Alle Rechnungen Schritt für Schritt erklärt
- LV124 oder VDA Band 3 Teil 2 verstehen
- Grundlagen der Zuverlässigkeitstechnik
- Lastkollektive auswerten und ableiten
- FMEA verstehen und anwenden
- Zuverlässigkeiten berechnen
- Erprobungen planen/auswerten
- Success Run Tests planen
