Unabhängig von der Art der Belastung (ob schwingend oder statisch) muss der statische Festigkeitsnachweis geführt werden. Dieser dient der Absicherung des Bauteils gegen Bruch und unzulässige plastische Verformungen.
Erfahren Sie in dieser Beitragsserie
- wie Sie einen statischen Nachweis für Ihre Bauteile führen und
- wie Sie ihr Bauteil höher auszulasten, indem Sie plastische Dehnungen im Kerbgrund zulassen.
Der erste Artikel konzentriert sich auf das Werkstoffverhalten und die Berechnung der Beanspruchungen (Spannungen). Dieser zweite Artikel befasst sich dann mit dem eigentlichen Festigkeitsnachweis.
Berechnung der Beanspruchbarkeit
Beim konventionellen Festigkeitsnachweis werden die im Zugversuch ermittelten Werkstoffkennwerte als ertragbare Beanspruchbarkeit σert herangezogen. Dies sind die Zugfestigkeit Rm und die Streckgrenze Re. Beide Werkstoffkennwerte werden unabhängig von der Belastungsart (Zug/Druck, Biegung, Schub oder Torsion) verwendet. Eine Auslegung von Bauteilen erfolgt immer gegen Fließen und Bruch. Erreichen die Kerbspannungen die Streckgrenze Re, muss mit unzulässigen Verformungen des Bauteils gerechnet werden. Überschreiten die Kerbspannungen die Zugfestigkeit Rm, droht der Bruch des Bauteils. Die ertragbaren Beanspruchbarkeiten sind damit:
| σert,Fließen= Re | (1) |
| σert,Bruch= Rm | (2) |
Tragreserven heben:
Insbesondere bei gekerbten Bauteilen treten die maximalen Spannungen stark konzentriert in den Kerben auf. Überschreiten dann die Kerbspannungen die Streckgrenze, plastifiziert der Werkstoff lokal eng begrenzt. Mit einer globalen Verformung oder dem Versagen des Bauteiles ist nicht zu rechnen.
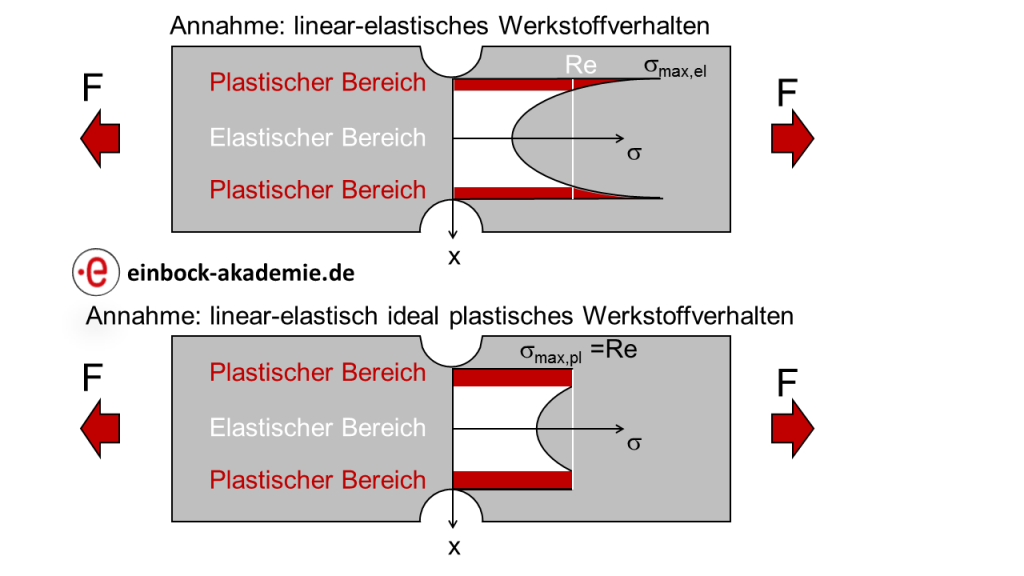 Abbildung 1: Spannungsverlauf bei Plastifizierungen des Werkstoffes |
Abbildung 1 zeigt schematisch den Spannungsverlauf im Bauteil. Das obere Bild stellt den Spannungsverlauf bei Annahme des linear-elastischen Werkstoffverhaltens dar. Erkennbar ist, dass wegen der Kerbe nur ein kleiner Teil des Querschnittes plastische Verformungen aufweist, obwohl die maximalen Spannungen sehr deutlich oberhalb der Streckgrenze liegen. Im unteren Bild von Abbildung 1 ist der Spannungsverlauf bei Annahme des linearelastisch ideal-plastischen Werkstoffverhaltens schematisch skizziert. Da der Werkstoff bei Erreichen der Streckgrenze zu fließen beginnt, sind die maximalen Spannungen durch die Streckgrenze begrenzt.
Der Flächeninhalt der roten und weißen Fläche ist proportional zur Kraft F. Deshalb vergrößern sich die plastischen Bereiche (rote Fläche). Außerdem nehmen die Spannungen im elastischen Bereich (weißer Bereich) zu.
Es werden die hoch beanspruchten (plastisch verformten) Bereiche des Bauteils durch die noch elastisch beanspruchten Bereiche gestützt. Für den Festigkeitsnachweis können deshalb für die höchst beanspruchte Stelle plastische Dehnungen zugelassen werden à Stützwirkung.
Um diese Stützwirkung beim Festigkeitsnachweis zu berücksichtigen, wird die Streckgrenze um die plastische Stützzahl erhöht. Als ertragbare Beanspruchung gilt damit:
| σ*ert,Fließen= Re · npl | (3) |
Die plastische Stützzahl berechnet sich wie folgt:
| npl = (E · εert / Re)1/2 | (4) |
Es ist E der E-Modul des Werkstoffes und εert die im Kerbgrund plastisch ertragbare Dehnung unter Annahme linear-elastischen Werkstoffverhaltens.
Nach der FKM-Richtlinie* gelten die in Tabelle 1 angegebenen Werte für duktile Werkstoffe.
Tabelle 1: Ertragbare Dehnungen für duktile Werkstoffe
| Stahl | Alu Knetlegierung | Alu Guss | |
| εert in % | 5 | 5 | 2 |
Die Berechnung des plastischen Werkstoffverhaltens mittels FEM ist sehr aufwändig Für den Festigkeitsnachweis wird deshalb weiterhin mit den linear-elastischen Spannungen gerechnet.
Es muss bei diesem Vorgehen abgesichert werden, dass die Belastung nicht soweit gesteigert wird, dass der gesamte Querschnitt plastifiziert (es liegen also keine elastischen Bereiche mehr vor). Diese Absicherung erfolgt durch die vollplastische Formzahl Kp:
| Kp = (Lvollplastisch)/(Lelastisch) | (5) |
Dabei ist
Lvollplastisch die vollplastische Traglast (z.B. für Abbildung 1 die Kraft), bei welcher der gesamte Querschnitt plastifiziert und
Lelastisch die elastische Grenzlast (z.B. für Abbildung 1 die Kraft), bei der die Streckgrenze erreicht ist. Es gilt also σmax = Re.
Die Berechnung der vollplastischen Formzahl ist aufwändig und kann beispielsweise mittels FEM oder analytisch erfolgen. Für einfache Querschnitte gelten nach der FKM-Richtlinie* die Werte aus Tabelle 2.
Tabelle 2: Vollplastische Formzahlen
| Querschnitt | Biegung Kp,b | Torsion Kp,t |
| Kreis | 1,7 | 1,33 |
| Kreisring (dünnwandig) | 1,27 | 1 |
| Rechteck | 1,5 | - |
Um eine vollplastische Beanspruchung des Querschnitts zu vermeiden, wird der Festigkeitsnachweis wird stets mit dem Minimum aus plastischer Stützzahl npl und vollplastischer Formzahl Kp geführt.
Als ertragbare Beanspruchung gilt damit:
| σ*ert,Fließen= Re · MIN(Kp ; npl) | (6) |
Mit
| npl = (E · εert / Re)1/2 |
Und Kp nach Tabelle 2.
Berechnung der Sicherheit
Um Versagen mit Sicherheit ausschließen zu können, werden für den konventionellen Festigkeitsnachweis die ertragbaren Beanspruchbarkeiten mit Sicherheitsfaktoren und verrechnet. Als zulässige Spannung gilt:
| σzul,Fließen = (σert,Fließen)/SF = Re/SF | (8) |
| σzul,Bruch= (σert,Bruch)/SB = Rm/SB | (9) |
Übliche Sicherheitskennwerte für duktile Werkstoffe sind nach [1] abhängig von der Art des Versagens und der Schwere der Fehler, vgl. Tabelle 3.
Tabelle 3: Sicherheitsfaktoren für den statischen Festigkeitsnachweis
| Obere Zeile:SF Untere Zeile:SB | Schadensfolge | |||
| hoch | mittel | niedrig | ||
| Auftretenswahrscheinlichkeit der Kerbspannung | hoch | 2,0 1,5 | 1,85 1,4 | 1,75 1,3 |
| niedrig | 1,8 1,35 | 1,7 1,25 | 1,6 1,2 | |
Für duktile Werkstoffe können Tragreserven gehoben werden, indem ertragbare plastische Dehnungen im Kerbgrund zulassen werden. Es gilt dann für den Festigkeitsnachweis analog zu Gleichung (8) und (9) sowie mit Gleichung (6) gilt:
σzul,Fließen = (σ*ert,Fließen)/SF | (10) |
| σzul,Bruch= (σert,Bruch)/SB = Rm/SB | (11) |
Folgende Randbedingungen sind unbedingt einzuhalten:
- an der zu bewertenden Stelle ist die Spannungsverteilung über den Querschnitt nicht konstant,
- der Werkstoff ist ausreichend duktil (A>6 %),
- der Werkstoff kriecht nicht,
- die Sicherheit gegen Bruch ist ausreichend hoch
- der Bereich plastischer Dehnungen lokal eng begrenzt
Der eigentliche Festigkeitsnachweis erfolgt dann durch den Vergleich der wirkenden Kerbspannungen σmax mit den zulässigen Spannungen
σmax= Kt · σnenn,Fließen ≤ σzul,Fließen σmax= Kt · σnenn,Bruch ≤ σzul,Bruch | (12) (13) |
Leitfaden für eine Betriebsfestigkeitsrechnung: Empfehlungen zur Lebensdauerabschätzung von Maschinenbauteilen
Autoren: Gudehus, H.; Zenner, H.:
Neben den fachlichen Vorteilen ist außerdem der Preis sehr attraktiv.
Fazit: Für den Einstieg in die Betriebsfestigkeit absolut die Nr. 1.
Rechnerischer Festigkeitsnachweis für Maschinenbauteile: FKM-Richtlinie
Herausgeber: Forschungskuratorium Maschinenbau (FKM)
Größt mögliche Flexibilität ist damit gewährleistet.
Fazit: Für jeden, der einen Festigkeitsnachweis führen möchte, der richtlinienbasiert ist, genau das Mittel der Wahl. Einziger Wermutstropfen: man benötigt etwas Zeit und Ruhe sich in die Richtlinie einzuarbeiten. Die Empfehlung ist: nehmen Sie sich diese Zeit, es lohnt sich!