Unabhängig von der Art der Belastung (ob schwingend oder statisch) muss der statische Festigkeitsnachweis geführt werden. Dieser dient der Absicherung des Bauteils gegen Bruch und unzulässige plastische Verformungen.
Erfahren Sie in dieser Beitragsserie
- wie Sie einen statischen Nachweis für Ihre Bauteile führen und
- wie Sie ihr Bauteil höher auszulasten, indem Sie plastische Dehnungen im Kerbgrund zulassen.
Dieser erste Artikel konzentriert sich auf das Werkstoffverhalten und die Berechnung der Beanspruchungen (Spannungen). Der zweite Artikel befasst sich dann mit dem eigentlichen statischen Festigkeitsnachweis.
Werkstoffverhalten bei statischer Belastung
Üblicherweise wird das Werkstoffverhalten unter zügiger Belastung gemessen. Dazu werden zylindrische Probekörper (z. B. genormt in DIN 50 125) mit der Querschnittsfläche A und der Länge L0 durch eine Zugkraft F rein axial belastet (vgl. Abbildung 1).
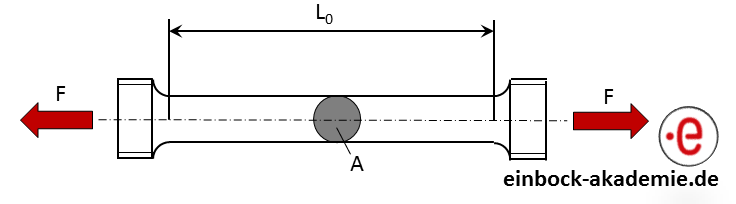
Abbildung 1: Zugprobe zur Ermittlung der statischen Werktsoffdaten
Als Reaktion auf die Kraft ergeben sich innere Beanspruchungen:
Spannung
Gleichung (1): σ = F/A in MPa
Dehnung
Gleichung (2): ε= ΔL / L0 in %
Im Rahmen eines Zugversuches (z.B. nach DIN EN 10 002) wird die Zugkraft bis zum Bruch des Probekörpers gesteigert. Es werden die Zugkraft F und die Längenänderung ΔL des Probekörpers gemessen und in Spannung und Dehnung umgerechnet.
Als Ergebnis erhält man das Werkstoffverhalten in Form des zügigen Spannungs-Dehnungs-Diagramms. Abbildung 2 zeigt dies schematisch für duktile / verformungsfähige Werkstoffe mit und ohne ausgeprägte Streckgrenze. Wichtige, für den Festigkeitsnachweis relevante Kennwerte sind nachfolgend aufgelistet.
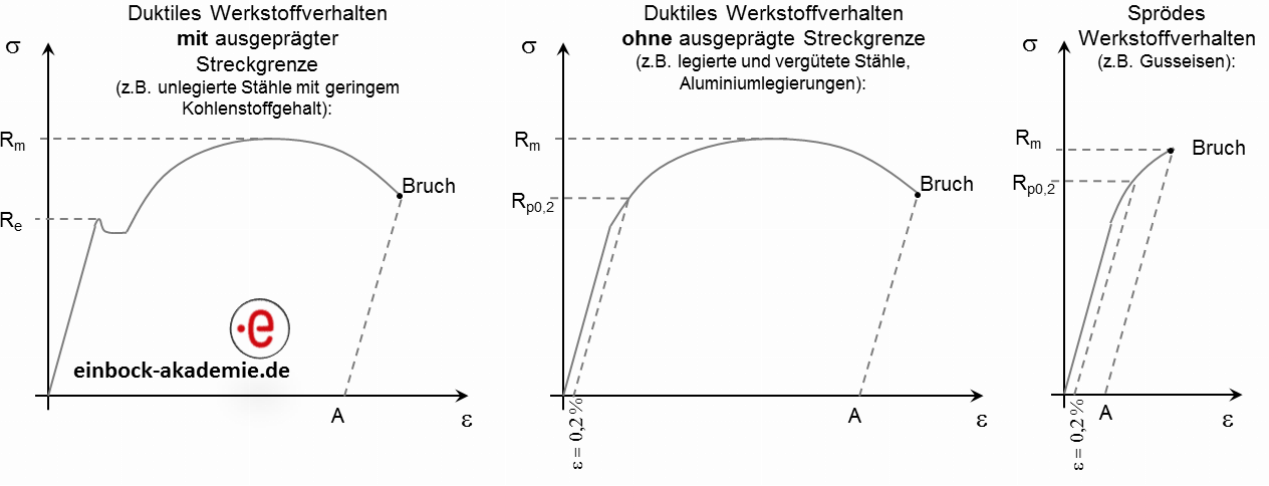
Abbildung 2: Schematische Darstellung der Spannungs-Dehnungs-Diagramme
Die Streckgrenze Re oder die Ersatzstreckgrenze Rp0,2
Liegt die Beanspruchung des Bauteiles unterhalb der Streckgrenze, verhält sich der Werkstoff nach dem Hook’schen Gesetz linear-elastisch. Eine bleibende Verformung des Werkstoffes tritt nicht auf. Spannung und Dehnung hängen über den E-Modul voneinander ab:
Gleichung (3): σ=E · ε
Typische Werte für den E-Modul sind nach FKM-Richtlinie*
Aluminiumlegierungen : 70 000 N/mm2
Stähle: 210 000 N/mm2
Eisengusswerkstoffe: 180 000 .. 190 000 N/mm2
Typische Werte für die Streckgrenze können Werkstoffkatalogen entnommen werden. Siehe auch https://www.einbock-akademie.de/download für eine Auswahl von Datenbanken.
Vereinfachend wird teilweise mit linear-elastischem ideal-plastischem Werkstoffverhalten gearbeitet. Dabei wird angenommen, dass sich der Werkstoff bis zur Höhe der Streckgrenze linear-elastisch verhält und danach keine weitere Verfestigung mehr erfährt. Diese Annahme ist für spröde Werkstoffe nicht gültig. Siehe folgende Abbildung:
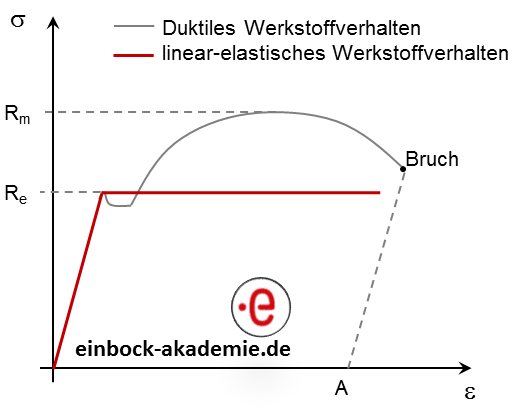
Abbildung 3: Linearelastisch-ideal plastisches Werkstoffverhalten (schematisch)
Die Zugfestigkeit Rm
Überschreiten die Spannungen die Streckgrenze beginnt der Werkstoff zu plastifizieren. Ein Entlasten des Werkstoffes führt zu einer bleibenden, plastischen Verformung. Das Erreichen der Zugfestigkeit Rm markiert die maximal ertragbare Spannung.
Typische Werte für die Zugfestigkeit können Werkstoffkatalogen entnommen werden. In https://www.einbock-akademie.de/download finden Sie eine Auswahl von Datenbanken.
Die Bruchdehnung A
Die gesamte bist zum Bruch ertragbare Dehnung wird als Bruchdehnung bezeichnet. Sie ist ein wesentliches Merkmal zur Identifizierung duktiler, d.h. verformungsfähiger Werkstoffe. Liegt die Bruchdehnung A > 6 % spricht man üblicherweise von duktilen Werkstoffen vgl. FKM-Richtlinie*
Berechnung der Beanspruchungen
Die Beanspruchung (Spannungen und Dehnungen) im Werkstoff wird für den statischen Nachweis linearelastisch nach Gleichung (3) berechnet. Allgemein gilt, dass die Spannungen von der Belastung und der Geometrie abhängt. Für den zylindrischen Stab hängt die Spannung von der Kraft (Belastung) und der Querschnittsfläche (Geometrie) siehe Gleichung (1). Bauteile weisen üblicherweise noch Kerben wie beispielsweise eine Verjüngung des Querschnitts, Bohrungen oder Einschnitte auf. Diese Kerben führen zu einem weiteren Einfluss der Geometrie: dem Kerbeinfluss. Unterschieden werden Nennspannungen und Kerbspannungen.
Nennspannungen berücksichtigen den Einfluss der Belastung und der Geometrie, vernachlässigen aber die Kerbeinflüsse. Es werden vier Grundbelastungsfälle unterschieden. Basierend auf diesen Grundbelastungsfällen werden die Nennspannungen nach den in Abbildung 4 angegebenen Gleichungen berechnet. Vom Grundbelastungsfall ist die Geometriegröße abhängig. Für Zug/Druck und Schub ist dies der Querschnitt. Für Biegung und Torsion sind dies Widerstandsmomente. In Abbildung 5 fasst die Gleichungen der Widerstandsmomente ausgewählter Querschnitte zusammen.
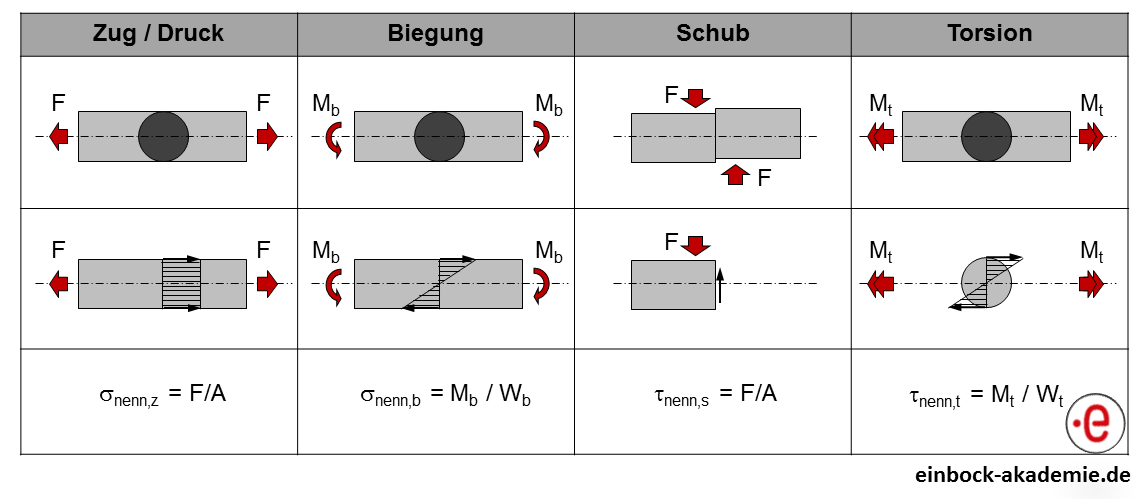
Abbildung 4: Berechnung der Nennspannungen für die Grundbelastungesfälle
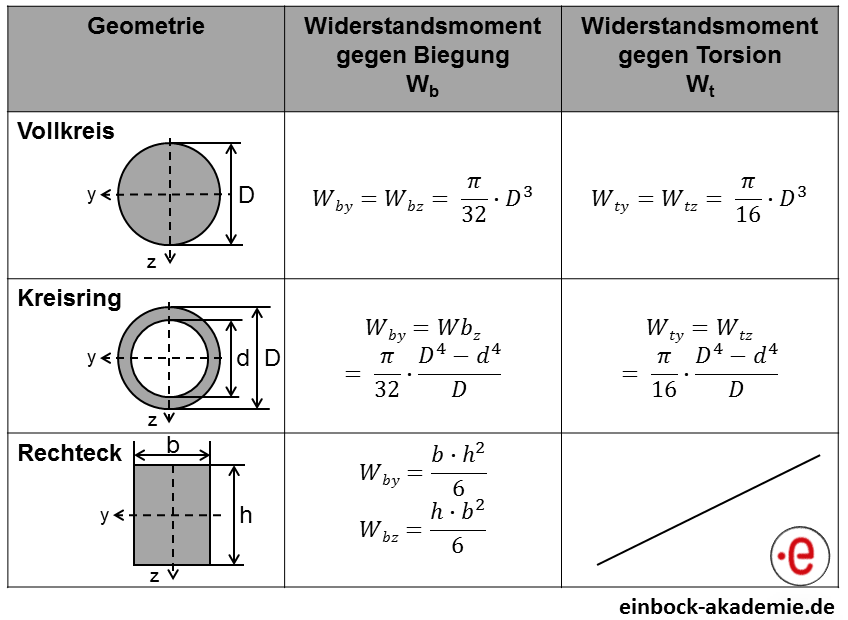
Abbildung 5: Widerstandsmomente ausgewählter Querschnitte
Kerbspannungen resultieren aus z.B. Verjüngungen des Bauteils. Diese Verjüngungen (Kerben) führen zu einer Spannungskonzentration in der Kerbe. D.h. Sie sind um Formzahl gegenüber den Nennspannungen erhöht. Es gilt üblicherweise Kt = 1,5..5. In Abbildung 6 ist für die Fälle Zug/Druck und Biegung der Zusammenhang zwischen Nennspannung und Kerbspannung dargestellt. Bei der Berechnung der Kerbspannungen geht man nach Abbildung 6 in zwei Schritten vor:
- Berechnung der Nennspannungen unter Vernachlässigung der Kerbe
- Berechnung der Kerbspannungen mit Hilfe der Formzahlen nach Abbildung 6
Gleichung (4): σmax = Kt · σnenn
Bei der Formzahl handelt es sich um eine von der Geometrie und Belastung abhängige Größe. Werte für die Formzahlen können Formzahldiagrammen entnommen werden (z.B. auf der Homepage der Hochschule Esslingen). Für Zug/Druck und Biegung liegen für die in Abbildung 6 dargestellten Geometrien gelten die in Abbildung 6 angegebenen Formeln.
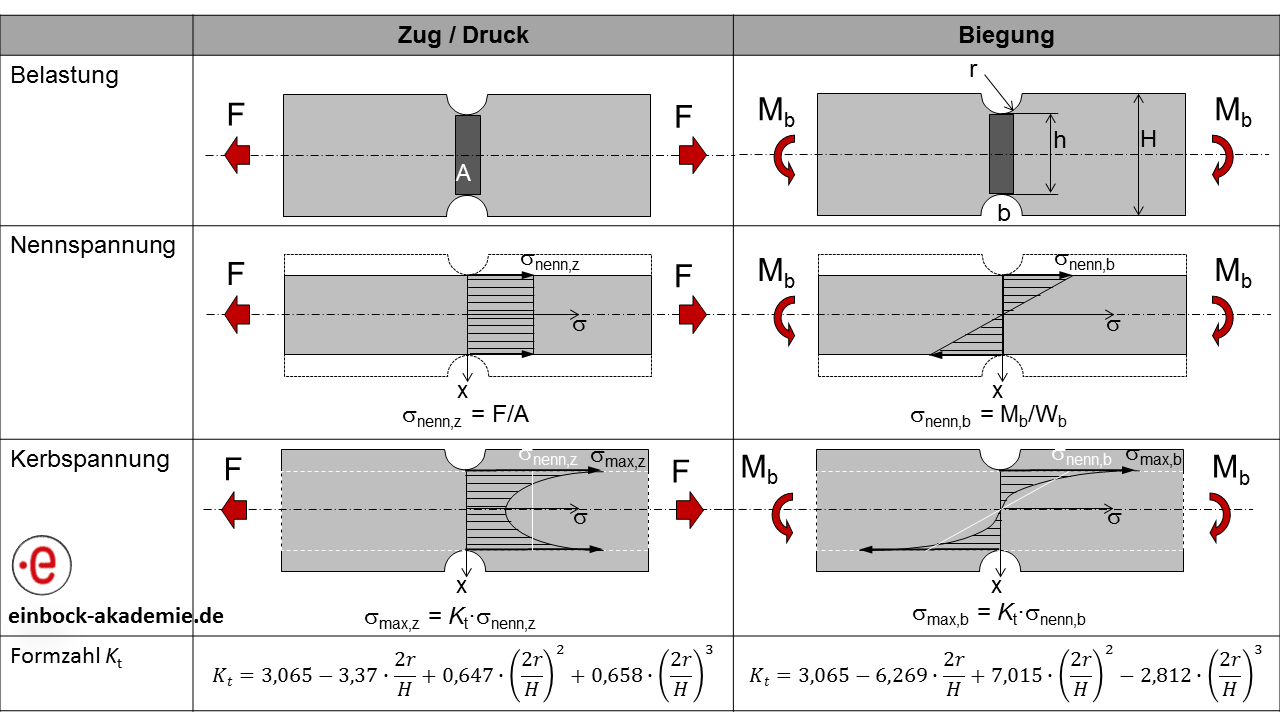
Abbildung 6: Zusammenhang zwischen Nennspannung und Kerbspannung inkl. Formeln zur Berechnung der Formzahlen
Alternativ zur vorgestellten Berechnung von Kerbspannungen über den analytischen Weg, können diese auch mittels FEM berechnet werden. Bei linear-elastischer Berechnung ist das Ergebnis der FEM direkt die Kerbspannung.
Ausgewertet werden dann üblicherweise für duktile Werkstoffe die Vergleichsspannung nach MISES und für spröde Werkstoffe die erste Hauptspannung.
Der Festigkeitsnachweis wird immer mit der Kerbspannung geführt
Autoren: Gudehus, H.; Zenner, H.:
Neben den fachlichen Vorteilen ist außerdem der Preis sehr attraktiv.
Fazit: Für den Einstieg in die Betriebsfestigkeit absolut die Nr. 1.
Herausgeber: Forschungskuratorium Maschinenbau (FKM)
Größt mögliche Flexibilität ist damit gewährleistet.
Fazit: Für jeden, der einen Festigkeitsnachweis führen möchte, der richtlinienbasiert ist, genau das Mittel der Wahl. Einziger Wermutstropfen: man benötigt etwas Zeit und Ruhe sich in die Richtlinie einzuarbeiten. Die Empfehlung ist: nehmen Sie sich diese Zeit, es lohnt sich!