Ausreisser in Messdaten bewerten. Teil 1: der Dean-Dixon Test auf Ausreisser
Arbeiten Sie auch mit experimentellen Daten? Dann haben Sie es sicherlich schon einmal mit Ausreißern zu tun gehabt. In diesem Fall stellen sich zwei Fragen: gibt es ein eindeutiges Kriterium, nach dem Ausreißer identifiziert werden können? Und: wie geht man mit Ausreißern um? Beide Fragen klären wir in dieser Artikelserie.
In diesem Artikel lernen Sie, wie Sie
In diesem Artikel führen wir
- die wichtigsten Begriffe ein und
- erklären was ein Ausreißer ist.
- Zusätzlich zeigen wir Ihnen einen statistischen Test zur Erkennung potenzieller Ausreisser, den Dean-Dixon Test. Zu dessen Anwendung stellen wir auch ein Excel Tool bereit.
Im zweiten Artikel besprechen wir dann den Umgang mit Ausreissern.
Inhalt
- Grundlagen Ausreisser
- Dean-Dixon Test
- Dean-Dixon mit Excel
- Alternativen
- Auf den Punkt
- Weitere Informationen
Grundlagen Ausreißer: Was ist das eigentlich?
Extremale Werte können die Auswertungen deutlich verzerren. Unterscheiden Sich diese Werte aus plausiblen Gründen (z. B. wegen eines anderen Effektes) von den restlichen Werten, können sie aus der Auswertung gestrichen werden. Man spricht dann von Ausreißern. Etwas anders formuliert, ist ein Ausreißer ein Wert, der sowohl in Hinsicht auf dessen Größe, als auch die Ursache deutlich von den erwarteten Werten abweicht.
Dies zeigt, dass die Bewertung von Ausreißern schwierig ist. Zum Einen muss festgelegt werden, was genau der Erwartungsbereich ist in dem die typischen Werte liegen. Zum Anderen muss definiert werden, ab welchem Abstand eines Wertes vom Erwartungsbereich dieser Wert als Ausreißer bewertet wird.
Das größte Risiko bei der Bewertung von Ausreißern ist, dass diese versehentlich aus den Auswertungen gestrichen werden und deswegen deutlich falsche Schlüsse aus einer Auswertung gezogen werden.
Dazu zwei Beispiele für Ausreißer
Das Ozonloch über der Arktis wurde viele Jahre gemessen. Allerdings wurden die Messungen als „falsch“ interpretiert und als Ausreißer definiert! Deswegen wurden die Auswirkungen des Ozonlochs nicht in seiner vollen Breite erfasst
Ähnliches vollzog sich in der Technik.
Die de Havilland Comet war das erste strahlgetriebene Verkehrsflugzeug der Welt. Dieses Flugzeug revolutionierte den Passagierflug, da sich die Reisezeiten halbierten und Flüge sehr komfortabel (leise und vibrationsarm) wurden.
In den Jahren 1953 bis 1954 stürzten drei Maschinen ab. Es gab dabei keine Überlebenden. Keines der Flugzeuge zeigte bis dahin irgendwelche Auffälligkeiten, die diesen Absturz erklären konnten. Der Ausfall der ersten Maschine wurde dem Wetter zugeschrieben. Ein systematischer Fehler wurde somit ausgeschlossen. Erst nach den weiteren Abstürzen wurde die Fehlersuche intensiviert (siehe auch unseren früheren Artikel: Link).
Arten von Ausreißern
Ein Ausreißer kann prinzipiell einer der folgenden Gruppen zugeordnet werden, es:
- ist schlicht Zufall. Bei allen streuenden Daten können rein zufällig extremale Werte auftauchen.
- handelt sich um einem Zahlendreher (anstelle von 13 wurde beim Datenübertrag 31 eingetragen).
- wurden versehentlich die falschen Daten eingetragen, Messsignale vertauscht oder es liegt ein Messfehler vor.
- gibt einen plausiblen physikalischen Grund, dass sich dieser Wert von den restlichen Werten unterscheidet.
Streng genommen handelt es sich bei den ersten drei Punkten nicht um Ausreißer, sondern um Extremwerte. Es gibt prinzipiell zwei Möglichkeiten um auf Ausreißer und Extremwerte zu reagieren.
Zum Einen kann die Datenauswertung mit Methoden erfolgen, die robust gegenüber Ausreißern sind. Zu nennen sind hier Kennwerte wie der Medianwert anstelle des Mittelwertes oder der Quartile anstelle der Standardabweichung.
Zum Anderen können potenzielle Ausreißer mit Hilfe statistischer Methoden gefunden werden. Genauer gesagt werden mit Hilfe statistischer Methoden Werte identifiziert, die statistisch signifikant von den restlichen Werten abweichen. Ob es sich tatsächlich um einen Ausreißer handelt, muss dann vom Bearbeiter durch eine separate Untersuchung geklärt werden. Häufig wird davon ausgegangen, dass sich die Stichprobenwerte zufällig nach der Normalverteilung (oder in der Betriebsfestigkeit nach der logarithmischen Normalverteilung) verteilen. Es wird angenommen, dass ein Wert als Ausreißer deklariert werden kann, wenn dieser statistisch signifikant von dieser Verteilung abweicht.
Der Ausreißer Test nach Dixon
Mit dem Test nach Dixon (oder auch Dean-Dixon) liegt ein sehr handlicher Test vor, der auch für kleine Stichproben anwendbar ist.
Vorrausetzungen des Tests nach Dixon sind:
- Die Stichprobe ist normalverteilt
- Der Test wird auf einen Datensatz nur einmal angewandt
Ob für die Daten eine Normalverteilung angenommen werden darf, muss überprüft werden. Dazu können Sie unsere Wahrscheinlichkeitsnetze nutzen: Wahrscheinlichkeitsnetze für Excel.
Liegen die Daten hier näherungsweise auf einer Geraden, dann darf eine Normalverteilung angenommen werden.
Schritt 1 (Formulierung der Nullhypothese für den Ausreißertest)
Die Nullhypothese H0 und Alternativhypothese H1 werden wie folgt formuliert. Zur Formulierung der Nullhypothese finden Sie hier noch weitere Informationen.
H0: x1 ist kein Ausreißer
H1: x1 ist ein Ausreißer
Es ist darin x1 der zu analysierende Wert. Dies kann entweder der kleinste oder der größte Wert der Stichprobe sein.
Zusätzlich ist noch die gewünschte Signifikanz α des Testergebnisses festzulegen. Üblich ist α = 5%.
Schritt 2 (Berechnung der Prüfgröße Q des Dixon Tests)
Soll der kleinste Wert der Stichprobe analysier werden, dann wird die Stichprobe vom kleinsten zum größten Wert der Größe nach sortiert. Soll dagegen der größte Wert bewertet werden, wird die Stichprobe vom größten zum kleinsten Wert geordnet:
x1 ≤ x2 ≤ x3 ≤... ≤ xn-2 ≤ xn-1 ≤ xn , wenn der kleinste Wert interessiert und
x1 ≥ x2 ≥ x3 ≥... ≥ xn-2 ≥ xn-1 ≥ xn , wenn der größte Wert interessiert.
Abhängig von dem Stichprobenumfang n erfolgt die Berechnung der Prüfgröße Q:
Q = Q10 = (x1 - x2)/(x1 - xn) für 3 ≤ n ≤ 8
Q = Q11 = (x1 - x2)/(x1 - xn-1) für 8 ≤ n ≤ 11
Q = Q21 = (x1 - x3)/(x1 - xn-1) für 11 ≤ n ≤ 14
Q = Q22 = (x1 - x3)/(x1 - xn-2) für n > 14
Schritt 3 (Testentscheidung des Dixon Ausreißer Tests):
Abhängig von der Stichprobengröße und der Signifikanz α wird die Prüfgröße mit dem kritischen Wert verglichen. Die Nullhypothese H0 wird verworfen, wenn die Prüfgröße Q oberhalb, bzw. rechts des kritischen Wertes Qn,α nach folgender Tabelle liegt:
Q > Qn,α → Nullhypothese wird verworfen, der Wert ist ein Ausreißer
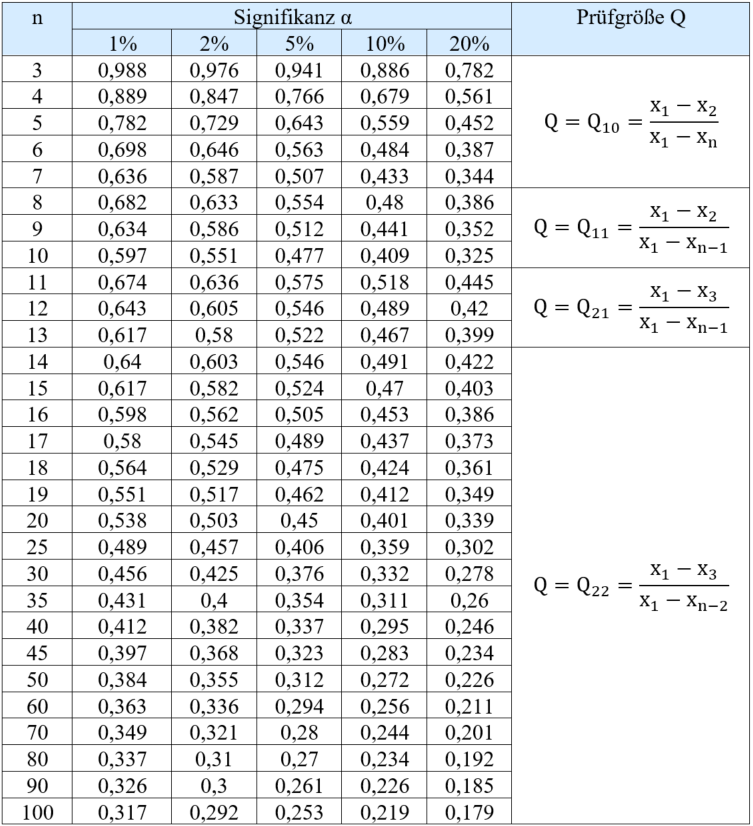
Kritische Werte Q des Dean-Dixon Ausreißer Tests
Ein Beispiel für die Anwendung des Ausreißer Tests
Es wurde an 10 Proben die Zugfestigkeit Rm eines Bauteils gemessen. Die Werte sind in folgender Tabelle dokumentiert. Überprüft werden soll, ob der 10. Messwert von den anderen Werten mit einer Signifikanz von α = 5% abweicht.
Gemessene Zugfestigkeit Rm in MPa
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xj | 859 | 758 | 842 | 877 | 888 | 666 | 656 | 745 | 858 | 1148 |
Schritt 1 (Formulierung der Nullhypothese)
Die Nullhypothese H0 und Alternativhypothese H1 werden wie folgt formuliert
H0: ist kein Ausreißer
H1: ist ein Ausreißer
Schritt 2 (Berechnung der Prüfgröße)
Da der größte Wert der Messung bewertet werden soll, werden die Daten vom größten zum kleinsten Wert sortiert. Siehe dazu unten:
Der Größe nach sortierte Messwerte der Zugfestigkeit in MPa
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xi | 1148 | 888 | 877 | 859 | 858 | 842 | 758 | 745 | 666 | 656 |
Da die Stichprobe n=10 Werte umfasst, wird die Prüfgröße folgendermaßen berechnet:
Q = Q11 = (x1 - x2)/(x1 - xn-1) = (11,48 - 8,88) / (11,48-6,66) = 0,54.
Schritt 3 (Testentscheidung):
Die Prüfgröße Q11 = 0,54 wird für n = 10 und α = 5 % mit dem kritischen Wert nach obiger Tabelle verglichen. Es gilt:
Q11 = 0,54 > Q10,5% = 0,447.
Deshalb wird der Wert mit einer Signifikanz von 5% als Ausreißer erkannt. Ob und vor allem, warum dieser Wert tatsächlich von den anderen Abweicht, dazu liefert die Statistik keine Aussage. Das ist Aufgabe des Ingenieurs. Das ist doch beruhigend, oder? Wir sind trotz Rechnern und Statistik nicht ersetzbar;)
Für den Fall, dass dieser Wert tatsächlich von den anderen Abweicht, darf er aus der Statistik entfernt werden.
Dean-Dixon Ausreisser Test mit Excel
In unserem Downloadbereich finden Sie außerdem noch das kostenlose Excel Tool für den Dean-Dixon Ausreisser Test um Ihre Daten schnell und einfach auf Ausreißer testen zu können.
Download: Ausreißer Test nach Dean-Dixon mit Excel
Die untere Abbildung zeigt einen Screenshot des Tools.
Dazu noch ein Hinweis: der Ausreißertest befindet sich im Excel-Tool für die Wahrscheinlichkeitsnetze.
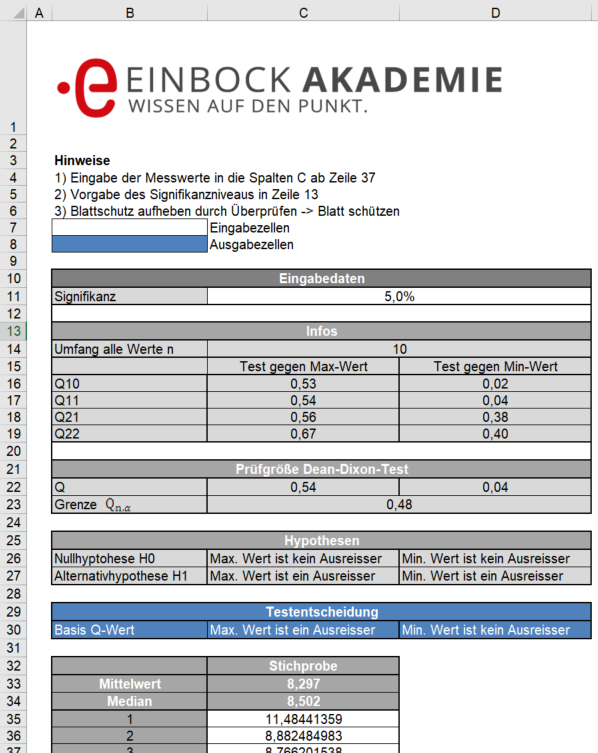
Screenshot der Excel Tools des Dean-Dixon Ausreisser Tests
Alternative Ausreißertests
Als Alternative zu dem Ausreißertest nach Dixon können noch folgende weitere Tests genannt werden:
- Ausreißertest nach Grubbs (als direkte Alternative zum Dixon Test)
- Ausreißertests nach Pearson (für große Stichproben)
- Ausreißterest nach Walsh (für nicht normalverteilte Daten)
Auf den Punkt
- Ein Ausreißer ein Wert, der sowohl in Hinsicht auf dessen Größe, als auch die Ursache deutlich von den erwarteten Werten abweicht.
- Ausreißer können das Ergebnis stark beeinflussen.
- Leichtfertiges Streichen von Ausreißer birgt das Risiko, kritische Einflüsse zu übersehen.
- Statistische Tests auf Ausreißer haben den Vorteil, dass sie "neutral" sind.
- Ein einfacher und praktischer Test auf Ausreißer ist der Dixon Test.
- Statistische Tests liefern keine Beweise, nur einen Hinweise!
- Den Beweis, dass es sich bei dem auffälligen Wert tatsächlich um einen Ausreißer handelt muss der Ingenieur durch klassische Ingenieursarbeit liefern.
In diesem Sinne: bleiben Sie wachsam;)
Weiterführende Informationen zur Auswertung von Wöhlerversuchen und Identifikation von Ausreissern
Hier finden Sie ähnliche Artikel und Informationen zu passenden Seminaren und Büchern. Außerdem können Sie den Inhalt des Artikels bewerten.Bewerte den Artikel!
[yasr_visitor_votes size="medium"]
Seminar Werkstoffkennwerte der Betriebsfestigkeit (für Simulation und Auslegung) einfach ermitteln und anwenden
Wollen Sie Ihre Versuche so kostengünstig wie möglich und mit der geringsten Anzahl an Versuchen durchfürhen? Dann ist evtl. unsere Wöhlerlinien auswerten und Versuche planen für Sie richtig.
Sie lernen hier,
- wie Sie Wöhlerversuche und Dauerfestigkeitsversuche mit geringst möglichem Stichprobenumfang durchführen
- Wöhlerlinien und Dauerfestigkeiten statistisch auszuwerten
- Ausreißer zu finden und mit Ausreißern umzugehen
- Versuche aus der Vergangenheit zu nutzen
- mit sehr geringen Stichprobenumfängen umzugehen
- Sicherheiten für Ihre Bauteilauslegung abzuleiten
- zwei Wöhlerlinien statistisch miteinander zu vergleichen
- einen kurzen Einstieg in die Betriebsfestigkeit kennen.
Weiterführende Literatur

Um Wöhlerkurven und Dauerfestigkeiten statistisch auszuwerten und zu planen, bietet sich außerdem unser
Buch Statistik der Betriebsfestigkeit an.
dieses führt Sie schnell und verständlich in die Versuche und die Statistik Betriebsfestigkeit ein und liefert gleichzeitig noch viele Excel Tools zur einfacheren Auswertung von Versuchen der Betriebsfestigkeit wie Wöhlerlinien. Hier erfahren Sie auch mehr Details zum Umgang mit Ausreissern.
